nLab cosmic cube
Context
Higher category theory
Basic concepts
Basic theorems
- homotopy hypothesis-theorem
- delooping hypothesis-theorem
- periodic table
- stabilization hypothesis-theorem
- exactness hypothesis
- holographic principle
Applications
Models
- (n,r)-category
- Theta-space
- ∞-category/∞-category
- (∞,n)-category
- (∞,2)-category
- (∞,1)-category
- (∞,0)-category/∞-groupoid
- n-category = (n,n)-category
- n-poset = (n-1,n)-category
- n-groupoid = (n,0)-category
- categorification/decategorification
- geometric definition of higher category
- algebraic definition of higher category
- stable homotopy theory
Morphisms
Functors
Universal constructions
Extra properties and structure
1-categorical presentations
Contents
- Idea
- Vertices of the cube
- Strict -categories
- Strict -groupoids
- Stably monoidal -categories
- Stably monoidal -groupoids
- Strictly stably monoidal strict -groupoids
- Etc.
- Edges of the cube
- Strict -groupoids in all -groupoids
- Strictly stable strict -groupoids in strict -groupoids
- Strictly stable strict -groupoids in all -groupoids
- Strictly stable strict -groupoids in strictly stable -groupoids
- Strictly stable -groupoids in all -groupoids
- References
Idea
The Cosmic Cube of higher category theory is the name for a diagram whose vertices correspond to special types of n-categories. The cube looks like this:
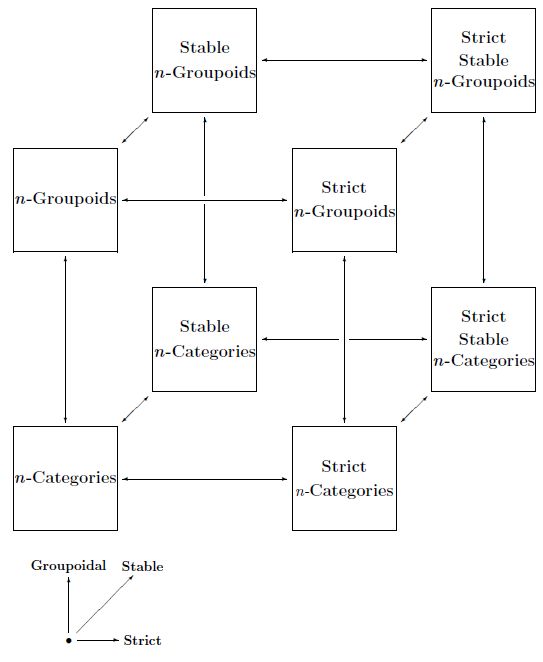
We may take here as well, and we may also consider a version for (n,r)-categories. The three axes correspond to:
-
making -categories ‘groupoidal’ — that is, making morphisms invertible, thus passing from general -categories to n-groupoids;
-
making -categories strict, thus passing from general -categories to strict -categories;
-
making -categories symmetric monoidal or ‘stable’, thus passing from general -categories to symmetric monoidal -categories.
In terms of homotopy theory
Each vertex of the cube can also be understood as corresponding to a version of homotopy theory:
-groupoids yield ordinary homotopy theory, symmetric monoidal and groupal -groupoids correspond to stable homotopy theory, strictly abelian strict -groupoids correspond to homological algebra. -Categories that are not -groupoids correspond to directed homotopy theory.
Vertices of the cube
Here we list the 8 vertices of the cube in the case of -categories.
Strict -categories
Strict -groupoids
Stably monoidal -categories
Stably monoidal -groupoids
Strictly stably monoidal strict -groupoids
Etc.
(…)
Edges of the cube
Strict -groupoids in all -groupoids
A strict ∞-groupoid is modeled by a crossed complex. Under ∞-nerve it embeds into all ∞-groupoids, modeled as Kan complexes.
Strictly stable strict -groupoids in strict -groupoids
A strictly stable strict ∞-groupoid is modeled by a bounded-below chain complex of abelian groups. Under the embedding of complexes into crossed complexes it embeds into strict ∞-groupoids.
For the definition of see Nonabelian Algebraic Topology , section Crossed complexes from chain complexes.
Strictly stable strict -groupoids in all -groupoids
Combining the above inclusions
yields in total the map from chain complexes to simplicial abelian groups (followed by the forgetful ) of the Dold-Kan correspondence.
Strictly stable strict -groupoids in strictly stable -groupoids
A strictly stable strict ∞-groupoid is modeled by a bounded-below chain complex of abelian groups. Under ∞-nerve it embeds into all (connective) spectras, modeled as spectrum objects in Kan complexes.
Strictly stable -groupoids in all -groupoids
A strictly stable ∞-groupoid is modeled by a connective spectrum. The forgetful functor to ∞-groupoids is also called or the “zeroth-space functor.”
References
-
Some blog discussion
Last revised on October 6, 2010 at 22:55:34. See the history of this page for a list of all contributions to it.