Eric Forgy Delooping
Eric: Basically the images below were my attempt to illustrate the diagram
using just one “”.
However, after a light bulb occurred in the discussion of the “commutative walking square” at finite category, I think I might have a better understanding. If that is true, it means my illustrations were horrible.
I was never very comfortable with the squares containing a 2-cell, but I think I got it now. It should have been obvious, but never underestimate my ability to get confused with the obvious.
The way I would think of the diagram above now is that you have a 2-cell from the single functor
to itself. When I saw two composed arrows, I was failing to compose them and think of them as a single arrow with a 2-cell connecting the single arrow to itself. Instead, I was trying to think of as somehow relating all four arrows. GULP!
If I were to draw the diagrams again, I might draw just a single composite arrow with a 2-loop.
My second diagram

is closest to being correct, but I would now rotate the 2-arrows by 90 degrees and label the top one and the bottom one with
However, even then I would not be happy because my complaints about multiple ‘s representing the same object should carry over to multiple arrows representing the same functor, so to be perfectly explicit, I might write
with two 2-loops and as above.
In other words, just like I prefer to see 1-loops depicted like
as opposed to
I’d prefer to see 2-loops depicted as something like
with acknowledgment it is not very pretty :)
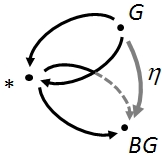
delooping of a group to a groupoid
Let be a group regarded as a discrete groupoid in the (∞,1)-topos ∞Grpd of ∞-groupoids.
Then exists and is, up to equivalence, the groupoid
-
with a single object ,
-
with , or equivalently ,
-
and with composition of morphisms in being given by the product operation in the group.
More informally but more suggestively we may write
or
to emphasize that there is really only a single object.
Notice how the homotopy pullback works in this simple case:
the universal 2-cell
filling this 2-limit diagram is the natural transformation from the constant functor
to itself, whose component map
is just the identity map, using that and .
Discussion
Eric: Thanks. Maybe I read too much into choices of notation, but I can sort of see why you prefer if you are accustomed to thinking in terms of . They look the same! My brain is wired to think of , so I prefer (because they look the same). Maybe there is no connection. I know it is irrelevant, but just a random observation :)
Urs: Well, the main reason is that one doesn’t get very far with any computation or any nontrivial statement when not allowing oneself to write several s, even though they all denote the same object. Try drawing the naturality squares of the natural transformations that appear in the above discussion without using several copies of the point!
And notice that in every other context, you wouldn’t hesitate to use several copies of one symbol that denotes the same variable. Try writing an equation with many s in it by writing all the s on the same spot. All you’d get is an unreadable mess. Nobody would ever complain that in the two s are really the same and should hence be drawn on the same spot.
Remarkably, I should add that I had this discussion before with professional pure mathematicians. Once they stopped a talk I gave when I wrote to the board, complaining that Ii drew two copies of that bullet. If it’s just about saying quickly what is like that’s fine with me, but for doing anything nontrivial with it it becomes useless. Try drawing for a 2-group or a 3-group! Not to speak of drawing the transformations between functors between these.
Eric: Here is an attempt to convert one of your diagrams above to a single version.
I’m not saying one way is better than the other. I’m just making a statement about my inability to process some of the diagrams. Some diagrams are not even amenable to these “3d projections”, but for those that can be, it would help me to convert them.
Eric: Here is another attempt in case that one is not quite right…

Toby: I think that perhaps part of the problem is that people see ?‘ as a generic placeholder like ?’; notice that the two dashes in ?‘ below do not refer to the same thing! (With ?’, you know that the two copies refer to the same thing, else one of them would be ?‘ instead.) So perhaps people need to be told that the bullet is like a letter and not like a dash.
Along those lines, sometimes it's nice to use ?‘ itself in place of the bullet. Ultimately, you can think of this as Cayley's Theorem: every group acts on itself (somewhat ambiguously on the left or on the right). Then with , you have a picture of as a subcategory of Set, consisting of the underlying set of as the only object and the functions given by the action of the elements of on that set as the morphisms.
Urs: I have to admit that I don’t quite understand Eric’s pictures. Here is what I meant concerning the transformation:
let be two group homomorphisms and be a natural transformation between the corresponding functors . Then has a single component to be denoted , which is required to make the naturality square
commute, for all . You can’t draw such diagrams when insisting that all the points appearing here are to be drawn on the same spot.
And, yes, as Toby indicates, we could give that point any other name, which maybe makes that more manifest. Let’s call it , then we have
and the desire to draw all s on the same spot should diminish yet a bit more.