nLab cosmological constant
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Cosmology
Contents
Idea
In theories of gravity and cosmology a cosmological constant refers to an energy contribution associated with the vacuum itself.
This is called a cosmological constant because the simplest way to see this effect in theory is by a summand to the Einstein-Hilbert action which is proportional to the volume of spacetime, with proportionality factor some “constant” , as in (1) below.
See below
More generally, almost-constant contributions to matter fields may effectively have the same kind of effect.
Specifically in perturbative quantum field theory on curved spacetimes the vacuum expectation value of the stress-energy tensor of the various matter-fields receives constant or essentially constant contributions, notably from renormalization freedom (e.g. Hack 15, section 3.2.1).
See below
In perturbative string theory the string perturbation series associated with a 2d SCFT is (supposedly) UV-finite and hence has “chosen its own renormalization” already, hence here the cosmological constant may in principle be read off from a choice of perturbative string theory vacuum. See below
Observation shows that the effective cosmological constant of the observable universe is comparatively small but positive, see
Details
In classical gravity
In an action functional on a space of pseudo-Riemannian manifolds – such as the Einstein-Hilbert action functional for gravity – a cosmological constant is a term proportional to the volume
where is the cosmological constant .
For instance, pure Einstein-Hilbert gravity with cosmological constant (and no other fields) is given by the functional
Generically it happens that one considers action functionals where is in fact not a constant, but a function of other fields on .
In this context those solutions to the Euler-Lagrange equations are of interest in which happens to be exactly or approximately constant. Many such models of not-really-constant-but-effectively-constant terms proportional to the volume are being proposed and considered in attempts to explain observed or speculated dynamics of the cosmos.
See in particular at FRW model for the role of the cosmological constant in homogeneous and isotropic models as in the standard model of cosmology. In that context the cosmological constant is also called the dark energy (density), which makes up about 70% of the energy density of the observable universe (the rest being dark matter) and a comparatively little bit of baryonic matter.
In perturbative quantum gravity
In perturbative quantum field theory on curved spacetimes the cosmological constant receives contributions from the vacuum expectation value of the stress-energy tensor of the matter fields. There is renormalization-freedom in this contribution (Wald 78, Tichy-Flanagan 98 Moretti 01).
Explicitly for FRW models this is discussed in (Dappiaggi-Fredenhagen-Pinamonti 08, Dappiagi-Hack-Moeller-Pinamonti 10). Specifically for the standard model of cosmology see (Hack 13, around (4)).
A useful review is in (Hack 15, section 3.2.1).
This means that apart from the freedom of choosing a classical comsological constant in the Einstein-Hilbert action as above, its perturbative quantization (perturbative quantum gravity) introduces renormalization freedom to the value of the cosmological constant.
The folklore discussion of the “cosmological constant problem” (see the references below) tends not to take this freedom in the theory into account (see the discussion at naturalness).
In inhomogeneous cosmology
It has been suggested the observed cosmological constant/dark energy may be but an artifact of the overly idealistic approximation of cosmic homogeneity, and that a more accurate inhomogeneous cosmology would not need to assume any dark energy (e.g. Buchert 07, Buchert 11, Buchert-Rasanen 11, Scharf 13).
A seminal argument that it is consistent to neglect cosmic inhomogeneity due to (Green-Wald 10, Green-Wald 13), has been called into question in Buchert et al. 15, where it is concluded that the question is more subtle and remains open. Recent review is in Belejko-Korzyński 16.
If the apparent small positive cosmological constant were but an artifact of neglecting backreaction of inhomogeneities, some theoretical puzzlement regarding quantum gravity on de Sitter spacetimes would disappear (see Rajaraman 16 for general discussion and Danielsson-VanRiet 18, p. 27 for discussion of perturbative string theory vacua).
Observation
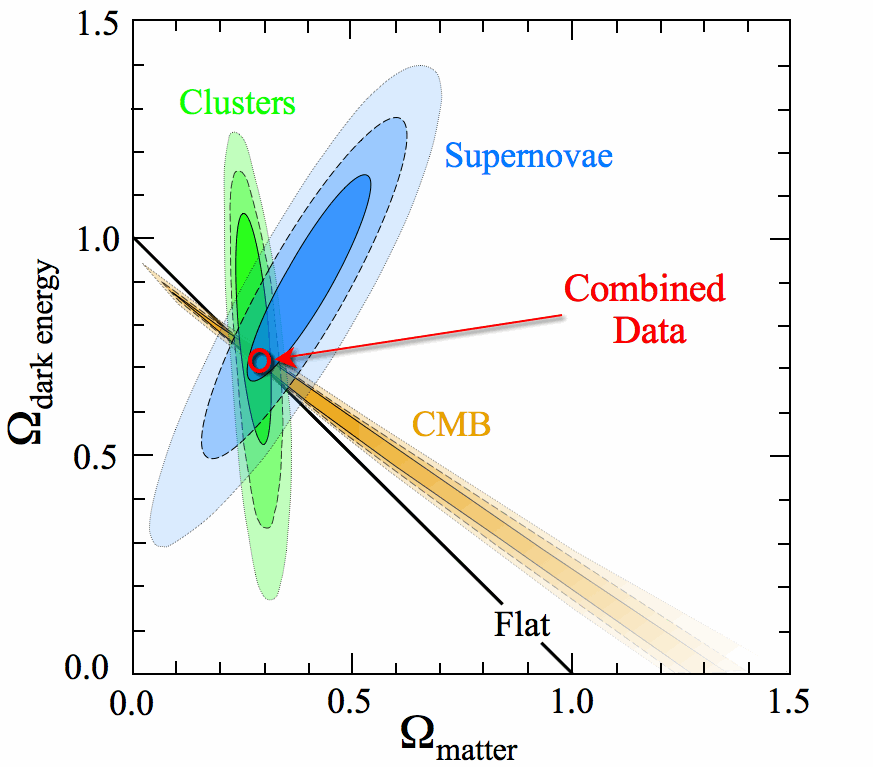
(e.g. Einasto 09, fig 17)
Related concepts
References
General
Introduction and review:
- Konstantinos Xenos, An Introduction to FRW Cosmology and dark energy models (arXiv:2101.06135)
Careful discussion in perturbative quantum gravity:
- John Donoghue, The cosmological constant and the use of cutoffs (arXiv:2009.00728)
Tests
Tests to constrain the value of the cosmological constant are developed in:
-
David Benisty, Anne-Christine Davis, N. Wyn Evans, Constraining Dark Energy from Local Group dynamics, The Astrophysical Journal Letters, Volume 953, Number 1, August 8, 2023. (doi:10.3847/2041-8213/ace90b, arXiv:2306.14963)
-
David Benisty, Jenny Wagner, Denitsa Staicova, Dark Energy as a Critical Period in Binary Motion: Bounds from Multi-scale Binaries (arXiv:2310.11488)
Observation
(…)
Non-Observation
Cautioning against the interpretation of type Ia supernovae as indicative of a small positive cosmological constant (de Sitter spacetime) as in the current standard model of cosmology includes the following (see also at inhomogeneous cosmology and at Witten's Dark Fantasy):
-
Subir Sarkar, Is the evidence for dark energy secure?, Gen. Rel. Grav. 40:269-284, 2008 (arXiv:0710.5307)
-
J. T. Nielsen, A. Guffanti & Subir Sarkar, Marginal evidence for cosmic acceleration from Type Ia supernovae, Nature Scientific Reports volume 6, Article number: 35596 (2016) (arXiv:1506.01354, web discussion)
-
Koushik Dutta, Ruchika, Anirban Roy, Anjan A. Sen, M.M. Sheikh-Jabbari, Negative Cosmological Constant is Consistent with Cosmological Data (arXiv:1808.06623)
-
Rui-Yun Guo, Jing-Fei Zhang, Xin Zhang, Can the tension be resolved in extensions to ΛCDM cosmology? (arXiv:1809.02340)
-
Yijung Kang, Young-Wook Lee, Young-Lo Kim, Chul Chung, Chang Hee Ree, Early-type Host Galaxies of Type Ia Supernovae. II. Evidence for Luminosity Evolution in Supernova Cosmology, Astrophysical Journal (arXiv:1912.04903)
exposition:
New evidence shows that the key assumption made in the discovery of dark energy is in error
-
Eleonora Di Valentino, Alessandro Melchiorri, Joseph Silk, Cosmic Discordance: Planck and luminosity distance data exclude LCDM (arXiv:2003.04935)
(preferring phantom dark energy)
-
Roya Mohayaee, Mohamed Rameez, Subir Sarkar, Do supernovae indicate an accelerating universe? (arXiv:2106.03119)
In pAQFT
Discussion of the cosmological constant in the rigorous formulation of perturbative AQFT on curved spacetimes includes the following.
The freedom of renormalization of the vacuum expectation value of any stress-energy tensor, hence of the cosmological constant, was discussed in
- Robert Wald, Trace anomaly of a conformally invariant quantum field in curved spacetime, Phys. Rev. D 17, 1477 1978 (doi:10.1103/PhysRevD.17.1477)
Notice that (Wald 78) is based on
- Robert Wald, The back reaction effect in particle creation in curved spacetime, Commun. Math. Phys. (1977) 54: 1. (doi:10.1007/BF01609833)
which claimed no freedom of renormalization, but Wald 78 explains that this was due to a mistake inherited from a citation.
Further development of this includes
-
Wolfgang Tichy, Eanna E. Flanagan, How unique is the expected stress-energy tensor of a massive scalar field?, Phys.Rev. D58 (1998) 124007 (arXiv:gr-qc/9807015)
-
Valter Moretti, Comments on the Stress-Energy Tensor Operator in Curved Spacetime, Commun. Math. Phys. 232 (2003) 189-221 (arXiv:gr-qc/0109048)
A useful review is in
- Thomas-Paul Hack, section 3.2.1, Cosmological Applications of Algebraic Quantum Field Theory in Curved Spacetimes, Springer 2016 (arXiv:1506.01869, doi:10.1007/978-3-319-21894-6)
Realization of renormalization of stress-energy/cosmological constant in concrete FRW models is discussed in
-
Claudio Dappiaggi, Klaus Fredenhagen, Nicola Pinamonti, Stable cosmological models driven by a free quantum scalar field, Phys. Rev. D77:104015, 2008 (arXiv:0801.2850)
-
Claudio Dappiaggi, Thomas-Paul Hack, Jan Möller, Nicola Pinamonti, Dark Energy from Quantum Matter (arXiv:1007.5009)
Discussion specifically for the standard model of cosmology is in
- Thomas-Paul Hack, The Lambda CDM-model in quantum field theory on curved spacetime and Dark Radiation (arXiv:1306.3074)
More on subtleties of renormalization of the cosmological constant:
- John Donoghue, The cosmological constant and the use of cutoffs (arXiv:2009.00728)
From higher curvature corrections
Effective dark energy from higher curvature corrections, as in the Starobinsky model of cosmic inflation:
-
Michal Artymowski, Zygmunt Lalak, Inflation and dark energy from gravity, JCAP09(2014)036 (arXiv:1405.7818)
-
Michal Artymowski, Zygmunt Lalak, Marek Lewicki, Inflation and dark energy from gravity (arXiv:1510.04864)
From inhomogeneous cosmology
Discussion of the cosmological constant as an artefact of inhomogeneous cosmology (see there for more) includes the following
-
Thomas Buchert, Dark Energy from structure: a status report, Gen.Rel.Grav.40:467-527, 2008 (arXiv:0707.2153)
-
Stephen R. Green, Robert Wald, A new framework for analyzing the effects of small scale inhomogeneities in cosmology, Phys.Rev.D83:084020, 2011 (arXiv:1011.4920)
-
Thomas Buchert, Toward physical cosmology: focus on inhomogeneous geometry and its non-perturbative effects, Class.Quant.Grav.28:164007, 2011 (arXiv:1103.2016)
-
Thomas Buchert, Syksy Rasanen, Backreaction in late-time cosmology, Annual Review of Nuclear and Particle Science 62 (2012) 57-79 (arXiv:1112.5335)
-
Stephen Green, Robert Wald, Examples of backreaction of small scale inhomogeneities in cosmology, Phys.Rev.D87:124037, 2013 (arxiv:1304.2318)
-
Günter Scharf, Inhomogeneous cosmology in the cosmic rest frame without dark stuff, chapter 6 in the latest edition of Quantum Gauge Theories – A True Ghost Story, Wiley 2001 (arXiv:1312.2695)
-
Thomas Buchert et. al, Is there proof that backreaction of inhomogeneities is irrelevant in cosmology?, Class. Quantum Grav. 32 215021, 2015 (arXiv:1505.07800)
exposition in The Universe is inhomogeneous. Does it matter? CQG+, 2016
-
Krzysztof Bolejko, Mikołaj Korzyński, Inhomogeneous cosmology and backreaction: Current status and future prospects, Int. J. Mod. Phys. D 26, 1730011 (2017) (arXiv:1612.08222)
-
Ulf Danielsson, Thomas Van Riet, What if string theory has no de Sitter vacua? (arXiv:1804.01120)
See also at inhomogeneous cosmology.
The “cosmological constant problem”
Discussion of the experimentally observed tiny cosmological constant and the folklore theoretical problem with that includes the following
-
Subir Sarkar, New results in cosmology (arXiv:hep-ph/0201140)
-
Stefanus Nobbenhuis, The cosmological constant problem – an inspiration for new physics PhD thesis (2006) (web pdf)
-
Joan Sola, Cosmological constant and vacuum energy: old and new ideas, J.Phys.Conf.Ser. 453 (2013) 012015 (arXiv:1306.1527)
-
Ioanna Kourkoulou, Alberto Nicolis, Guanhao Sun, A technical analog of the cosmological constant problem and a solution thereof (arXiv:2101.11620, talk rec)
In string theory
Discussion from the point of view of perturbative string theory, where the cosmological constant is fixed by the choice of perturbative string theory vacuum.
For fundamentally vanishing cc (“Witten’s Dark Fantasy”)
An argument for non-perturbative non-supersymmetric 4d string phenomenology with fundamentally vanishing cosmological constant, based on 3d M-theory on 8-manifolds decompactified at strong coupling to 4d via duality between M-theory and type IIA string theory (recall the super 2-brane in 4d):
-
Edward Witten, The Cosmological Constant From The Viewpoint Of String Theory, lecture at DM2000 (arXiv:hep-ph/0002297)
(see p. 7)
-
Edward Witten, Strong coupling and the cosmological constant, Mod. Phys. Lett. A 10:2153-2156, 1995 (arXiv:hep-th/9506101)
-
Edward Witten, Section 3 of Some Comments On String Dynamics, talk at Strings95 (arXiv:hep-th/9507121)
This suggestion was called Witten's Dark Fantasy in Heckmann-Lawrie-Lin-Zoccarato 19, Section 8, where a concrete realization of this scenario in F-theory is claimed:
-
Cumrun Vafa, Section 4.3 of: Evidence for F-Theory, Nucl. Phys. B469:403-418, 1996 (arxiv:hep-th/9602022)
-
Jonathan Heckman, Craig Lawrie, Ling Lin, Gianluca Zoccarato, F-theory and Dark Energy, Fortschritte der Physik (arXiv:1811.01959, doi:10.1002/prop.201900057)
-
Jonathan Heckman, Craig Lawrie, Ling Lin, Jeremy Sakstein, Gianluca Zoccarato, Pixelated Dark Energy (arXiv:1901.10489)
For fundamentally non-vanishing cc
But a) there might be a large space of perturbative string theory vacua and b) the de Sitter vacua that seem to correspond to observation tend to exist (only) as metastable vacua:
- Shamit Kachru, Renata Kallosh, Andrei Linde, Sandip Trivedi, de Sitter Vacua in String Theory, Phys.Rev.D68:046005, 2003 (arXiv:hep-th/0301240)
This observation led to the discussion of the “landscape of string theory vacua”.
For review see
- Renata Kallosh, section 3 of de Sitter vacua and the landscape of string theory, J. Phys. Conf. Ser. 24 (2005) 87-110 (spire)
However, consistency problems of these arguments are raised in
- Ulf Danielsson, Thomas Van Riet, What if string theory has no de Sitter vacua? (arXiv:1804.01120)
Last revised on November 13, 2023 at 00:56:03. See the history of this page for a list of all contributions to it.