nLab pivotal symbols

The pivotal symbols or $3j$ symbols are a certain collection of signs attached to a fusion category arising from analyzing how invariant vectors in a $3$-particle state transform under rotation by a full revolution.

In a fusion category, the nature of duals for objects in the category can be encoded in principal $\mathbb{C}^\times$-bundle over the simple objects. Firstly, suppose one goes ahead and chooses an arbitrary dual object $V_i^*$ for every simple object $V_i$. Write

$$Dual(V_i \dashv V_i^*)$$

for the set of ways that $V_i^*$ can be expressed as a right dual of $V_i$. Notice that $Dual(V_i \dashv V_i^*)$ is a $\mathbb{C}^\times$-torsor (you can multiply the unit by a nonzero complex number, following which you are forced to multiply the counit by the reciprocal of this number if you want to obey the snake equations).

In a fusion category, if $V_i^*$ is a right dual of $V_i$, then it is also a left dual of $V_i$, though not in a canonical way. This gives us the principal $\mathbb{C}^\times$-bundle $L$ over the simple objects — the fiber above $V_i$ is

$$L_{V_i} = \left\{Dual(V_i \dashv V_i^*) \stackrel{\sim}\rightarrow Dual(V_i^* \dashv V_i) \right\},$$

the set of isomorphisms between $Dual(V_i \dashv V_i^*)$ and $Dual(V_i^* \dashv V_i)$.

A pivotal structure or even-handed structure is a section of this bundle satisfying some naturality properties. In other words, it is a consistent way to turn right duals into left duals. The most stringent condition is that the invariant vectors in a tensor product of three particles must either be totally ‘bosonic’ or totally ‘fermionic’ when you rotate them through a full rotation.

That is, the endomorphism

$$T_{ijk} : Hom(1,V_i \otimes V_j \otimes V_k) \rightarrow Hom(1,V_i \otimes V_j \otimes V_k)$$

(which can be proved to be an involution) given by sending

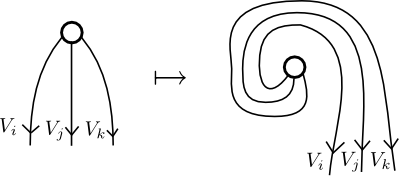
must be equal to $\pm id$. Assuming this is satisfied (if not, there is no consistent way to turn right duals into left duals), we can call this collection of signs the $3j$ symbols or the pivotal symbols $\epsilon_{ijk}$ of the fusion category:

$$T_{ijk} = \epsilon_{ijk} id.$$

That is to say, the $3j$ symbols are the signs arising from choosing a trivialization of the ‘duality bundle’ and analyzing how invariant $3$-particle tensors transform when they go through a full revolution.

It turns out that one can express the concept of a pivotal structure directly in terms of the pivotal symbols $\epsilon_{ijk}$. Namely, a pivotal structure on the category amounts to an $\epsilon$-twisted monoidal natural transformation? of the identity on the category. That is to say, a collection of nonzero complex numbers $t_{i}$ satisfying

$$t_j t_k = \epsilon_{ijk} t_i$$

whenever $V_i$ appears in $V_j \otimes V_k$. If all the $3j$ symbols were equal to $1$, this would just be an ordinary monoidal natural transformation of the identity. Perhaps this phenomenon can be understood in a more enlightening way using the language of planar algebras.

References

• P. Etingof, D. Nikshych and V. Ostrik, On fusion categories.
• T. J. Hagge and S-M Hong, Some non-braided fusion categories of rank 3.
• B. Bartlett, On unitary 2-representations of finite groups and topological quantum field theory (chapter 6).