nLab
worldline formalism

Idea

Traditionally the Feynman perturbation series/scattering amplitudes in perturbative quantum field theory are defined, given a free field vacuum and an local interaction action functional, by applying the Feynman rules (this prop.) to the monomial terms in the interaction Lagrangian density and deriving from that a rule for how to weight each Feynman diagram by a probability amplitude, its Feynman amplitude, subject to renormalization choices.

In contrast, in what is called the worldline formalism of perturbative quantum field theory this assignment is obtained instead more conceptually as the correlators/n-point functions of a 1-dimensional QFT that lives on the Feynman graphs, namely the worldline theory (usually a sigma-model in the given target spacetime) of the particles that are the quanta of the fields in the field theory.

One may think of this as making explicit the edges in a Feynman diagram as corresponding to virtual particles].

Mathematically the key step here is a Mellin transform – introducing a “Schwinger parameter” – which realizes the Feynman propagator $\Delta_F(x,y)$ as a path integral for a relativistic particle travelling from $y$ to $x$.

This worldline formalism is equivalent to the traditional formulation. It has the conceptual advantage that it expresses the Feynman perturbation series of perturbative quantum field theory manifestly as a second quantization of its particle content given explicitly as the superposition of all 1-particle processes.

The worldline formulation of QFT has an evident generalization to higher dimensional worldvolumes: in direct analogy one can consider summing the correlators/n-point functions over worldvolume theories of “higher dimensional particles” (“branes”) over all possible worldvolume geometries. Indeed, for 2-dimensional branes this is precisely the way in which perturbative string theory is defined: the string scattering amplitudes are given by the analogous “worldsheet formalism” known as the string perturbation series as the sum over all surfaces of the correlators/n-point functions of of a 2d SCFT of central charge 15.

worldvolume field theory	of fundamental branes	and their second quantization	which in perturbation theory is given by
worldline formalism	particle	quantum field theory	scattering amplitudes
2d CFT correlators	string	string field theory	string scattering amplitudes

Indeed, after decades of Feynman rules, the worldline formalism for QFT was found only via string theory in (Bern-Kosower 91), by looking at the point particle limit of string scattering amplitudes.

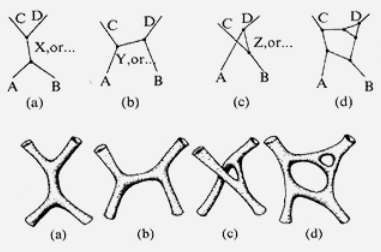
graphics grabbed from Jurke 10

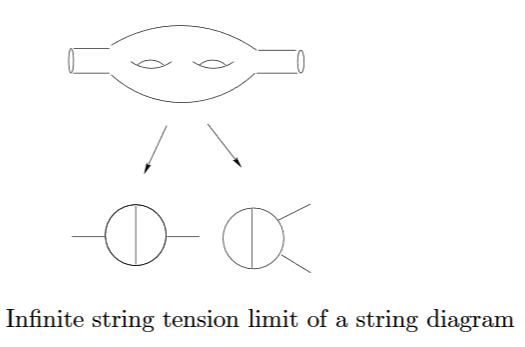
graphics grabbed from Schubert 96

Then (Strassler 92, Strassler 93) observed that generally the worldline formlism is obtained from the correlators of the 1d QFT of relativistic particles on their worldline.

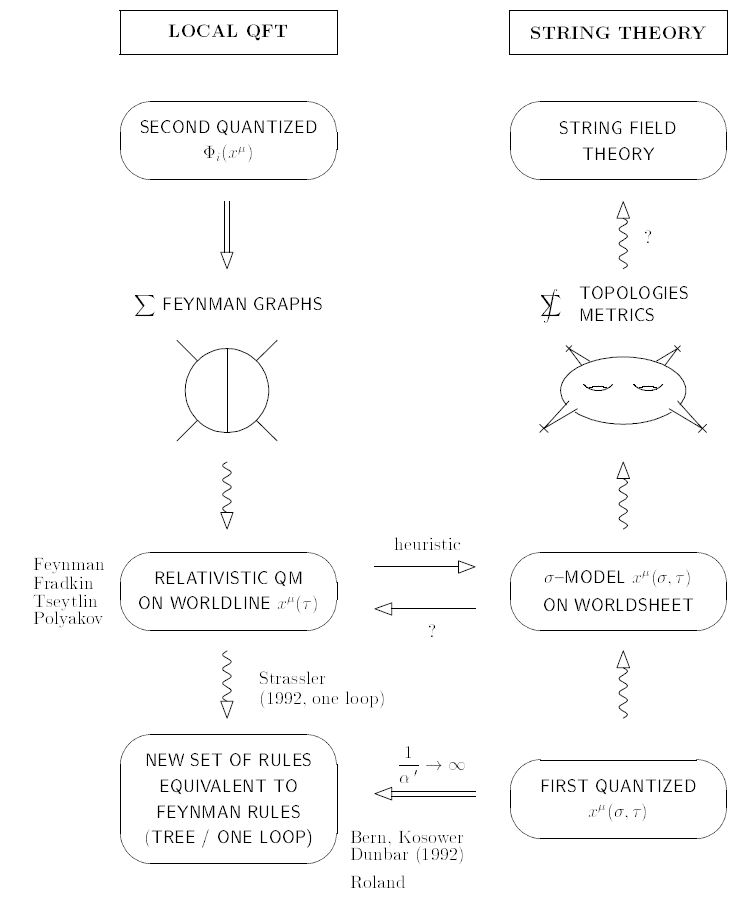
graphics grabbed from (Schmidt-Schubert 94)

The first calculuation along these lines was actually done earlier in (Metsaev-Tseytlin 88) where the 1-loop beta function for pure Yang-Mills theory was obtained as the point-particle limit of the partition function of a bosonic open string in a Yang-Mills background field. This provided a theoretical explanation for the observation, made earlier in (Nepomechie 83) that when computed via dimensional regularization then this beta function coefficient of Yang-Mills theory vanishes in spacetime dimension 26. This of course is the critical dimension of the bosonic string.

Related entries

• virtual particle

• string theory FAQ – What is the relationship between quantum field theory and string theory?

References

Precursor observations include

• R.I. Nepomechie, Remarks on quantized Yang-Mills theory in 26 dimensions, Physics Letters B Volume 128, Issues 3–4, 25 August 1983, Pages 177-178 Phys. Lett. B128 (1983) 177 (doi:10.1016/0370-2693(83)90385-4)

• Ruslan Metsaev, Arkady Tseytlin, On loop corrections to string theory effective actions, Nuclear Physics B Volume 298, Issue 1, 29 February 1988, Pages 109-132 (doi:10.1016/0550-3213(88)90306-9)

The worldline formalism as such was first derived from the point-particle limit of string scattering amplitudes in

• Zvi Bern, D. Kosower, Efficient calculation of one-loop QCD amplitudes Phys. Rev. D 66 (1991),(journal)

• Zvi Bern, D. Kosower, The computation of loop amplitudes in gauge theories, Nucl. Phys. B379 (1992) (journal)

Then it was related to actual worldline quantum field theory in

• Matthew Strassler, Field Theory Without Feynman Diagrams: One-Loop Effective Actions, Nucl. Phys. B385:145-184,1992 (arXiv:hep-ph/9205205)

• Matthew Strassler, The Bern-Kosower Rules and Their Relation to Quantum Field Theory, PhD thesis, Stanford 1993 (spires)

Reviews include

• M. G. Schmidt, Christian Schubert, The Worldline Path Integral Approach to Feynman Graphs (arXiv:hep-ph/9412358)

• Christian Schubert, An Introduction to the Worldline Technique for Quantum Field Theory Calculations, Acta Phys. Polon.B27:3965-4001, 1996 (arXiv:hep-th/9610108)

• Christian Schubert, Perturbative Quantum Field Theory in the String-Inspired Formalism, Phys.Rept. 355 (2001) 73-234 (arXiv:hep-th/0101036)

Exposition with an eye towards quantum gravity is in

• Edward Witten, from 30:40 on in Quantum Gravity, Solomon Lefschetz Memorial Lecture Series, November 2011 (video)

• Edward Witten, What every physicist should know about string theory, talk at Strings2015 (pdf, pdf, video recording)

Discussion of the Schwinger effect via worldline formalism:

• Gerald Dunne, Christian Schubert, Worldline Instantons and Pair Production in Inhomogeneous Fields, Phys. Rev. D72 (2005) 105004 (arXiv:hep-th/0507174)

Discussion for QCD with emphasis of 2d QCD and AdS/QCD:

• Adi Armoni, Oded Mintakevich, Comments on Mesonic Correlators in the Worldline Formalism, Nuclear Physics B, Volume 852, Issue 1, 1 November 2011, Pages 61-70 (arxiv:1102.5318)

Further development includes

• M. G. Schmidt, Christian Schubert, Worldline Green Functions for Multiloop Diagrams, Phys.Lett. B331 (1994) 69-76 (arXiv:hep-th/9403158)

• Eric D'Hoker, Darius G. Gagne, Worldline Path Integrals for Fermions with General Couplings, Nucl.Phys. B467 (1996) 297-312 (arXiv:hep-th/9512080)

• C. Alexandrou, R. Rosenfelder, A. W. Schreiber, Worldline path integral for the massive Dirac propagator: A four-dimensional approach, Phys. Rev. A59 (1999) 1762-1776 (arXiv:hep-th/9809101)

• Fiorenzo Bastianelli, Olindo Corradini, Andrea Zirotti, BRST treatment of zero modes for the worldline formalism in curved space, JHEP 0401 (2004) 023 (arXiv:hep-th/0312064)

• Peng Dai, Warren Siegel, Worldline Green Functions for Arbitrary Feynman Diagrams, Nucl.Phys.B770:107-122,2007 (arXiv:hep-th/0608062)

• S. A. Franchino-Viñas, S. Mignemi, Worldline Formalism in Snyder Spaces (arXiv:1806.11467)

• Olindo Corradini, Maurizio Muratori, String-inspired Methods and the Worldline Formalism in Curved Space (arXiv:1808.05401)

• Olindo Corradini, Maurizio Muratori, A Monte Carlo Approach to the Worldline Formalism in Curved Space (arXiv:2006.02911)

As a means of constructing UV-completions:

• Steven Abel, Nicola Andrea Dondi, UV Completion on the Worldline (arXiv:1905.04258)

For black hole scattering:

• Gustav Mogull, Jan Plefka, Jan Steinhoff, Classical black hole scattering from a worldline quantum field theory (arXiv:2010.02865)

A list of more literature is at

• The Tangent Bundle, QFT Worldline formalism