Eric Forgy Understanding Finite Limits

Ian’s Attempt

Ian: OK, here’s my attempt to simplify understand the notion of a limit. In the diagram, I only show one cone, but the assumption is that there are many and that all of them map to the limit in the same way (hence defining the limit).

Attempt #1

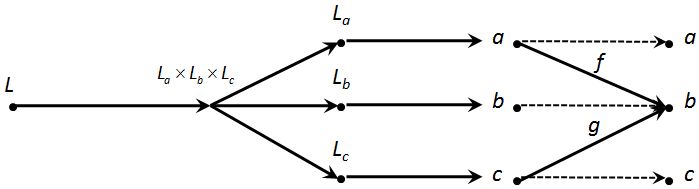
Over on the nForum, David Roberts gave an example of a limit of a diagram consisting of 4 objects $a$, $b$, $c$, and $d$ with 9 non-identity morphisms

$f_i:a\to b$

$g_j:a\to c$

$h_k:d\to c$

for $i,j,k = 1,2,3$. I suggested one way to look at this is to “extrude” the diagram, i.e. make two copies of the objects and extend each morphism from its domain in the first copy to the codomain in the second copy as illustrated below:

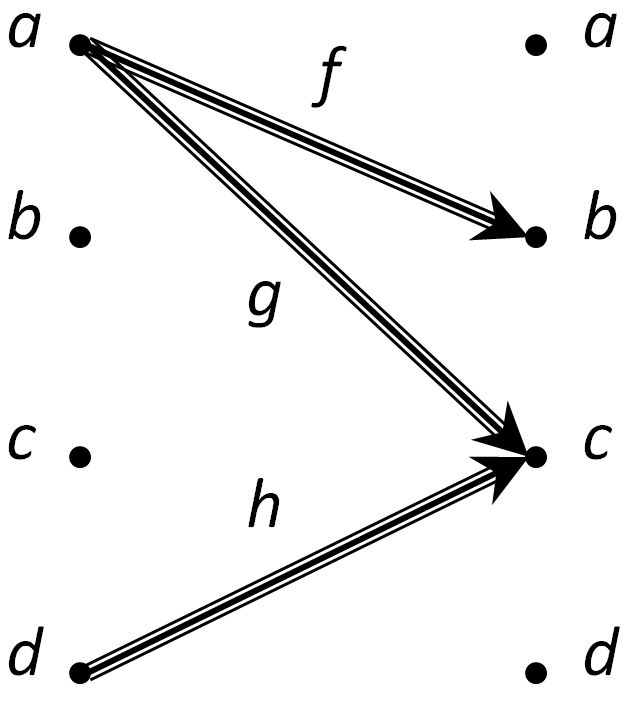
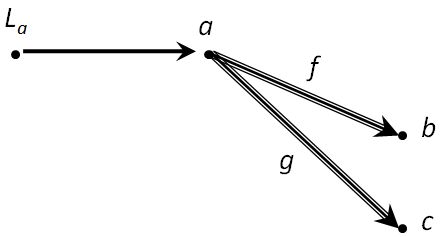
Now, if we consider the diagram whose “leaf” is object $a$, i.e. the subdiagram, then the limit of the subdiagram is the object that equalizes the $f$‘s and $g$’s simultaneously, i.e.

$f_1\circ L_a = f_2\circ L_a = f_3\circ L_a$

and

$g_1\circ L_a = g_2\circ L_a = g_3\circ L_a$

as illustrated below

Similarly, we have $L_d$ as the equalizer of the $h$‘s, i.e.

$h_1\circ L_d = h_2\circ L_d = h_3\circ L_d.$

For completeness, we could notationally let $L_b = b$ and $L_c = c$.

Now, I THINK the limit of the original diagram is the product of the sublimits, i.e.

$L = L_a\times L_b\times L_c\times L_d.$

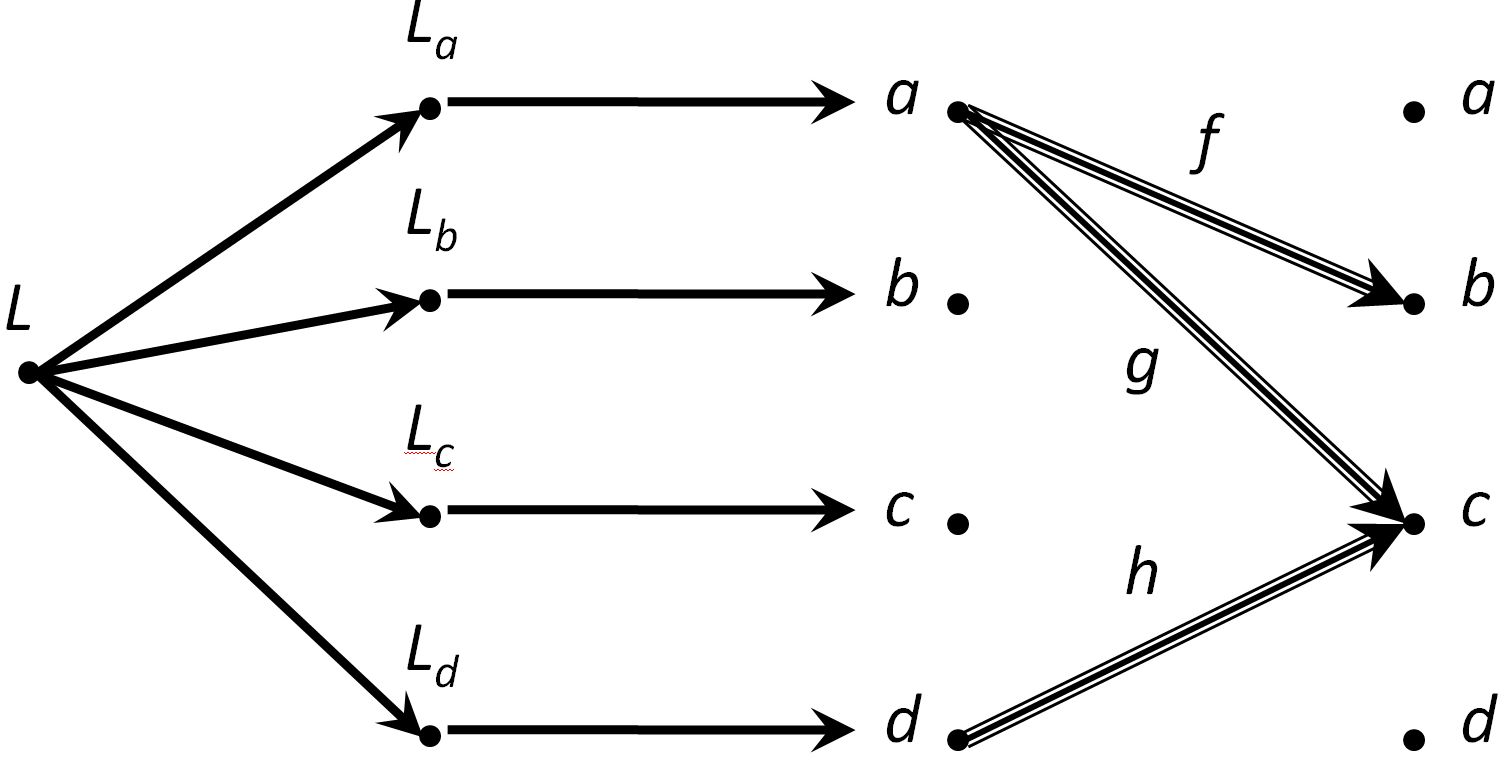
Bzzt. No. This does not work. I need to make sure it works for the pullback. The above does not give the correct pullback.

Some time later

Now that I’ve had a moment to think about this, I think the idea is correct, but I am simply missing a final equalizer on the left.

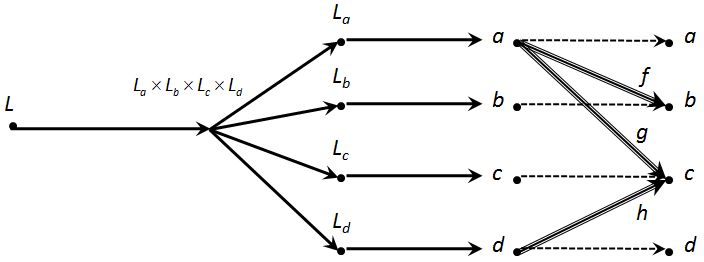
Note: The new dashed lines I’ve included are identity morphisms.

Let’s check with some examples…

Single object with no non-identity morphisms

It obviously works when the original diagram has just one object $a$ and no non-identity morphisms. In that case, the limit is just $a$.

Binary product

Since this procedure assumes you already know how to take products and equalizers to cook up a general finite limit, it might be instructive to look at a binary product, which should be a fairly degenerate recipe.

The illustration depicting the recipe applied to a binary product is show below.

Here, the limit $L_a$ of the $a$-subdiagram, i.e. the diagram reachable from object $a$, is simply $a$ itself as above. Similarly for $L_b$. Therefore,

$L_a\times L_b = a\times b.$

There are no parallel paths so the final step where you equalize everything is trivial too and we end up with

$L = a\times b$

as it should be.

So far so good.

Graph of a morphism

Next, consider the case where we have two objects and one non-identity morphism $f:a\to b$.

The recipe is now illustrated below.

Note: I guess the recipe requires you know how to compute products, equalizers, and graphs. But it is probably possible to think of a graph as a kind of degenerate equalizer.

The limit for the subdiagram whose leaf is $a$ is the graph

$L_a = \{a\times b|f\circ \pi_a = \pi_b\}.$

The subdiagram whose leaf is $b$ has no constraints so $L_b = b$. Therefore,

$L_a\times L_b = L_a\times b.$

Note that there are no constraints above on the projections $\pi_{L_a}$ and $\pi_{L_b}$ so the second $b$ above is free to wiggle around.

The final equalizer ties down the wiggling second $b$ by enforcing the constraint

$f\circ\pi_a\circ\pi_{L_a} = \pi_{L_b}$

so that

$L = \{L_a\times L_b| f\circ\pi_a\circ\pi_{L_a} = \pi_{L_b}\}.$

Unwrapping the above we have

$L = \{a\times b\times b|f\circ\pi_a = \pi^{(1)}_b, \pi^{(1)}_b = \pi^{(2)}_b\}$

where $\pi^{(i)}_b$ denotes the projection of the $i$th copy of $b$ so the second copy of $b$ is always the same as the first copy, so the limit $L$ is isomorphic to graph of $f$.

As it should be. So far so good.

Equalizer

The demonstration for the equalizer of a diagram $f,g:a\to b$ follows the exact same argument as for graphs except we have

$L_a = \{a\times b|f\circ\pi_a = \pi_b, g\circ\pi_a = \pi_b\}$

and the final equalizer enforces the constraints

$f\circ\pi_a\circ\pi_{L_a} = \pi_{L_b}$

and

$g\circ\pi_a\circ\pi_{L_a} = \pi_{L_b}$

so that

$f\circ\pi_a\circ\pi_{L_a} = g\circ\pi_a\circ\pi_{L_a}$

as it should be.

Pullback

The first real test of this recipe will be the pullback.

Ok. Now that I’ve done this a couple of times, the diagram chasing has become obvious.

This diagram says that

$f\circ\pi_a\circ\pi_{L_a} = g\circ\pi_c\circ\pi_{L_c} = \pi_{L_b}.$