Eric Forgy Process Calculus

Warning: This is draft material.

Goal

To understand process calculus arrow theoretically.

First, collect some concepts. We want to think of a concurrent system as a directed graph

• Nodes of the graph correspond to ordered events occurring on a processor

• An arrow from processor $A$ to processor $B$ indicates that a channel to transmit information from $A$ to $B$ is open

A processor is listening if it has edges directed toward it and is talking if it has edges directed away from it.

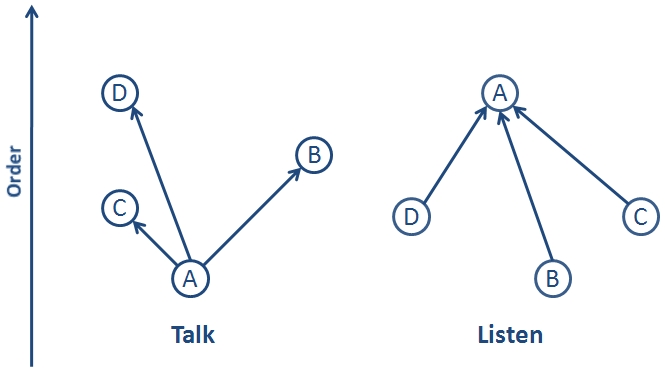
Any processor can be listening, talking, both, or neither.

Discussion

Note: This is extracted from a comment on the n-Cafe.

Eric: With ?process calculus? we obviously have ?processes? and ?processors?. What a processor does may depend on the order in which it receives information from some channel. I like the analogy of writing two checks for more than the bank balance and the outcome depends on which check is cashed first.

What I propose (without any claim of originality) is to try to think of ?process calculus? arrow theoretically where traversing each arrow requires a step through time. In other words, the picture should be that of a directed graph that looks reminiscent of a spacetime diagram. There should be a clear global concept of the ?flow of time?.

The significance of this is that statements like the following

can no longer be made.

Instead, to be explicit, you have to say something like:

With spacetime diagrams as a motivation, instead of saying ?Processor $A$ at time $t_0$?, we should think of the processor as a ?spacetime event? or ?node? in our directed graph. Then ?Processor $A$ at time $t_0$? is completely distinct from ?Processor $A$ at time $t_3$? since they are different points in spacetime and can have completely different behaviors depending on what has occurred between $t_0$ and $t_3$.

We have a bias toward thinking in terms of ?space? and not so much about ?spacetime?. The internet is a good example. You have computer $A$ talking to computer $B$ over channel $x$. You can take a picture of it and label it accordingly.

However, for computer $A$ to talk to computer $B$, it has to send information, which takes time. The ?channel? is not really a ?spacelike? link. It is a ?lightlike? link. Even though there is just one wire $x$ connecting the two computers there is really a series of channels for each time step. For example, at time $t_0$ there are two distinct channels

Therefore, the ?spatial? picture of two processors with one channel

needs to be replaced by the ?spacetime? picture

Note: This is a binary tree (or 2-diamond) with every even/odd transverse node identified, which can be thought of as a discrete version of the directed space $S^1\times\vec{I}$.

As time evolves, the directed graph evolves where channels/directed edges exist or not depending on the availability of the processor node they?re connecting to.

Sorry for this stream of consciousness. To understand $\pi$-calculus categorically, it would seem that a natural thing (and probably equivalent thing) to do is to understand it arrow theoretically. This was my initial attempt to maybe rephrase the question and start drawing some arrows.

John Baez: I think there?s something to what you say, Eric, but I think that most of these process calculi want to avoid assuming a ?global clock? that enables distant guys to agree on what time it is. So, no variable $t$ denoting time.

In a typical CPU you have a clock that keeps all the processes synchronized. But on the internet, things are more disorganized. So, most process calculi take a quite different attitude to time than you?re proposing. And an important aspect of the ∞-calculus is that you can say stuff like ?wait until you hear from me, then do blah-di-blah?.

That?s my impression at least. There are also asynchronous CPU?s that don?t have a central clock, but apparently they haven?t caught on.

Eric: I was a little nervous writing that, so thanks for being kind and taking the idea semi-seriously despite my presentation.

Whether or not the events are synchronized is not so important to the idea I was trying to outline I don’t think, but I do think that a notion of time is important for concurrency problems (from what little I understand). Things are always moving forward. Causality is manifest I think. Processor $B$ cannot receive a signal from processor $A$ before $A$ sends it, etc.

So although we could drop the ‘global clock’, I don’t know if we should drop time altogether. Although distant guys may not agree on what time it is, they should agree that event $A$ happened before event $B$. For this we simply need a preorder (which is niftily encoded in a directed graph).

So that I can kick the idea around without distracting from the conversation here, I created Process Calculus. Anyone interested in helping, please feel free to drop any notes there as well as here.

---

John Baez: The interview David mentioned is quite interesting to me, since as an outsider I really want to understand what all this abstract stuff is good for. I can?t resist quoting a bit? but I highly recommend reading the whole thing:

Steve Ross-Talbot: I left SpiritSoft in about 2001, because, like all start-ups, you have to focus on the things that you can deliver immediately, and SpiritSoft needed to focus on messaging, not on the high-level stuff that I very much wanted to do.

I got a dispensation to leave and do more work on event-condition-action, whereupon I met Duncan Johnston-Watt, who persuaded me to join a new company called Enigmatec.

At Enigmatec we went back to fundamentals. This really is the thread upon which the pi-calculus rests for me. When you do lots of event-condition-actions, if the action itself is to publish, you get a causal chain. So one event-condition-action rule ends up firing another, but you do not know that you have a causal chain?at least the system does not tell you.

It troubled me, for a considerable time, that this was somewhat uncontrollable, and certainly if I were a CIO and somebody said they were doing stuff and it?s terribly flexible, I?d be seriously worried about the fragility of my infrastructure with people subscribing to events and then onward publishing on the fly.

So causality started to trouble me, and I was looking for ways of understanding the fundamentals of interaction, because these subscriptions to events and the onward publishing of an event really have to do with an interaction between different services or different components in a distributed framework.

Many years before I did any of this, I studied under Robin Milner, the inventor of the pi-calculus, at Edinburgh University. I came back to the pi-calculus at Enigmatec and started to reread all of my original lecture notes, and then the books, and finally started to communicate with Robin himself. It then became quite obvious that there was a way of understanding causality in a more fundamental way.

One of the interesting things in the pi-calculus is that if you have the notion of identity so that you can point to a specific interaction between any two participants, and then point to the identity of an onward interaction that may follow, you?ve now got a causal chain with the identity token that is needed to establish linkage. This answered the problem that I was wrestling with, which was all about causality and how to manage it.

At Enigmatec, we told the venture capitalists we were doing one thing, but what we actually were doing was building a distributed virtual pi-calculus fabric in which you create highly distributed systems and run them in the fabric. The long-term aim was to be able to ask questions about systems, and the sorts of questions that we wanted to know were derived from causality. For example: Is our system free from livelocks? Is our system free from deadlocks? Does it have any race conditions?

These are the sorts of things that consume about half of your development and test time. Certainly in my experience the worst debugging efforts that I?ve ever had to undergo had to do with timing and resource sharing, which showed up as livelocks, deadlocks, and race conditions. Generally, what Java programmers were doing at the time to get rid of them, when they were under pressure, was to change the synchronization block and make it wider, which reduced the opportunity for livelocks and deadlocks. It didn?t fix the problem, really; what it did was alleviate the symptom.

Stephen Sparkes: Just made it slightly less likely to occur?

SR-T: That?s it. And I became obsessed with perfection, because I really felt you must be able to do this.

SS: It should be an absolute proof.

SR-T: Completely. We can prove something is an integer. Surely, we should be able to prove something about interaction. I started looking at other papers that leveraged the work of Robin Milner and the pi-calculus and found some fundamental work by Vasco Vasconcelos and Kohei Honda. Their work looked at something called session type, which, from a layman?s perspective, is this notion of identity tokens pre-pended to the interactions.

Layman?s perspective, eh? Anyway, I like the following passage a lot:

If you have that, then you can establish a graph a wait-for graph or a causality graph and statically analyze the program to determine whether it will exhibit livelocks, deadlocks, or race conditions.

I started to work with Kohei Honda on putting this into systems. That’s when the Choreography Working Group was established, and that’s when I became involved in the W3C.

It was quite natural to get the academics involved, which is why Robin Milner became an invited expert on that working group, along with Kohei Honda and Nobuko Yoshida. The three of them really formed the fulcrum for delivering these thoughts of very advanced behavioral typing systems, which the layman the programmer would never see. You would never need to see the algorithm. You would never need to read the literature unless you were having trouble sleeping at night.

That’s the only reason I can think of for people reading it, unless you want to implement it. It should be something that’s not there, in the same way that we don’t have to know about Turing completeness and Turing machines and lambda-calculus to write software. That’s all dealt with by the type system in general.

I managed to establish early on a bake-off between Petri net theory and the pi-calculus within the Choreography Working Group, and clearly the pi-calculus won the day. It won because when you deal with large, complex, distributed systems, one of the most common patterns that you come across is what we call a callback, where I might pass my details to you, and you might pass it to somebody else, in order for them to talk back to me. In Petri net theory, you can’t change the graph: it’s static. In the pi-calculus, you can. That notion of composability is essential to the success of any distributed formalism in this Internet age, where we commonly pass what are called channels in the pi-calculus, but we might call them URLs, between people. We do it in e-mails all the time, and we’re not conscious of what that may mean if there is automated computing at the end of the e-mail doing something with our URL that was just passed. There’s a real need to understand the formal side of things in order to have composability across the Internet, let alone within the domains of a particular organization.