nLab AndriusKulikauskas

Thank you for creating this space for research.

big picture?: My research at N Lab

At n Lab, I am interested to do a variety of personal and collaborative research projects regarding the big picture? in mathematics.

Category theory

I have twice tried to learn category theory and now will try for the third time. I am interested to learn it as a potential language for expressing an “algebra of perspectives”. Also, I think it is essential for understanding the “big picture” in mathematics as I’m hoping to do.

Learning category theory

• I’ve found the Catster videos especially helpful.
• I’m reading Wikipedia pages.
• I watched a series of video lectures on algebraic topology and that provided practical context.

My main interest

Since childhood I have wished to know everything and apply that knowledge usefully. I have written a summary of my findings, The Truth, From Relative to Absolute, which explains how to go from relative truth to absolute truth.

I am now writing a detailed book which I hope to finish next year. It will be a manual for investigators of the big questions in life. I want that to include big questions in math and physics. In particular, I want to explain how math and physics arise from more fundamental pre-mathematical perspectives.

My mathematical background

In educating myself, I earned Bachelor’s degrees in Math and Physics in 1986 from the University of Chicago and a Ph.D. in Math from UCSD in 1993. I took two courses on recursive function theory from Robert Soare at the University of Chicago.

For my Ph.D., my main interest was to study algebraic combinatorics as “the basement of math” from which mathematical objects arise, or so I thought. In algebraic combinatorics the symmetric functions are central because they are the generating functions for relabeling objects. I was particularly interested to know why among the infinitely many bases for the symmetric functions as a vector space there seemed to be six bases of particular interest to humans: the monomial, elementary, homogeneous, power, Schur and forgotten bases. I never answered this question. However, I realized that the determinant and trace of a generic matrix were symmetric functions of eigenvalues, and similarly, for my Ph.D. thesis, Symmetric functions of the eigenvalues of a matrix I calculated in terms of the matrix entries all six of these bases at the eigenvalues of a generic matrix. The usual symmetric functions are recovered by considering a diagonal matrix. Thus I had found a general framework for all of combinatorics in terms of matrix edges building up walks, signed cycles, words, Lyndon words, etc. But I ended my math research to focus on the philosophical questions about life which were my main interest.

My current interests in Math

discovery?

My current questions in math relate to my study in 2010-2011 of “the ways of figuring things out”. I surveyed 200 ways that I had figured things out in my philosophy and organized them into a system of 24 ways, a “house of knowledge”. I came up with an analogous system of 24 ways of figuring things out in mathematics which I wrote up here.

George Polya wrote a book “How to Solve It” where he describes several patterns for solving math problems, such as the pattern for “two locii”. For example, consider Euclid’s first problem in his Elements: In drawing an equilateral triangle, given the first side AB, how do we draw the other two? We solve this by drawing two circles of radius “AB” and noting their intersections. Now I noticed, let us consider what is happening in our minds! We are constructing a lattice of solution sets, namely, the two circles centered on A and B (each circle represents a condition), the points of intersection (they represent the set of both conditions) and the entire plane represents the set of no conditions. Thus in our minds we have reduced a nontrivial problem into a tiny lattice. That lattice is a mathematical object! We are using math to solve math. The math in the mind (the lattice) is much more basic than the math on the paper (the triangle). But the math in the mind is not defined in some explicit system, as far as we know. In some sense it is pre-systemic, pre-mathematical. It is a link between math and some more basic metaphysics. I went through Paul Zeitz’s excellent book “The Art and Craft of Problem Solving” and organized a system of 24 such mental math structures by which we figure things out. The system lets us see or at least imagine some of the origins of math, the distinctions of what is systemic and pre-systemic, what is algebra and what is analysis, what might be the most natural way of defining set theory axioms. Here are some 200 examples from math of ways of figuring things out:

Learning math for undersanding physics

For my book, I want to show how such a system can be set up fruitfully for any domain, any “world” as Heidegger would say, any “techne” as Aristotle would say. I think it’s important to try to do it for physics. So I’ve started going through the lists of physics experiments at Wikipedia. Also, here in Lithuania, I meet with Thomas Gajdosik, a theoretical physicist. I can ask him basic questions like, Why doesn’t an electron rip itself apart, given that like charges repel? I’ve realized that I need to learn a lot of math (Lie groups, Lie algebras) to understand physics. I need to learn things that I never understood (like tensors). So I have found some good books (such as “The Road to Reality” by Roger Penrose, available online for free), good video lectures (I like the ones by Fredric Schuller), and I find it very helpful to surf Wikipedia. I have also downloaded SageMath and will try that out to help me visualize and play with concrete structures. I feel that with these tools it’s possible to grasp the “big picture” in mathematics in a way that was not available in graduate school.

organization?

To get a sense of the big picture, I made a map of the areas of math based on the Mathematics Subject Classification:

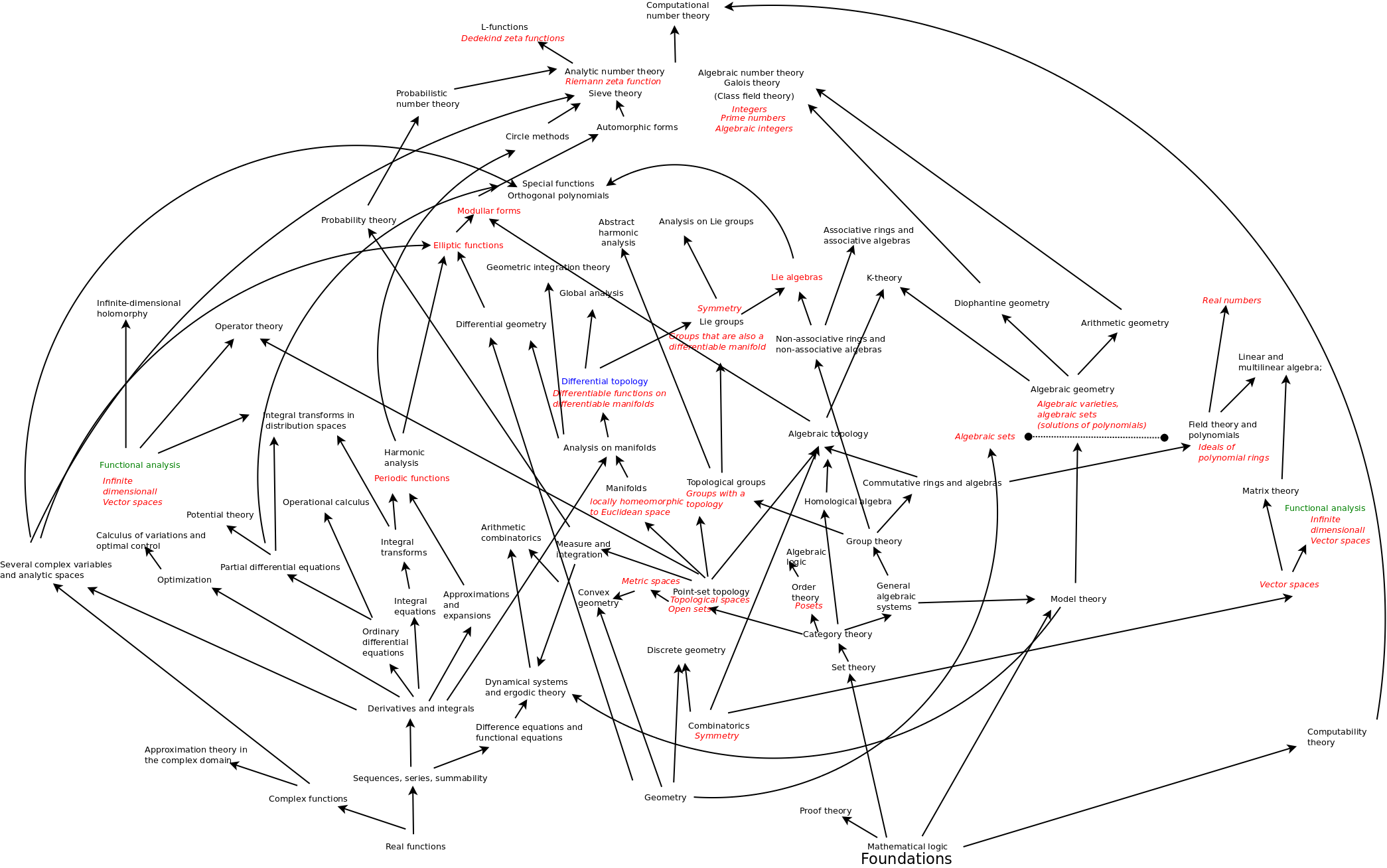
I organized them to try to show which area depended on which area. It’s just a first try but I wanted to see what was most basic in math. To my surprise, it seems that geometry must be very basic. So, for example, differential geometry is “calculus + geometry”, but what is geometry? I’m coming to believe that geometry is the way of embedding a lower dimension space into a higher dimension space. In particular, I think that this is what tensors are all about. I had been very confused about tensors trying to think of them as arrays of numbers, or “cemeteries” as Fredric Schuller says, critically, “witchcraft”. Now I am learning that the key point of tensors is that they divide a space into two points of view (covariant and contravariant). The most helpful picture for me is https://en.wikipedia.org/wiki/Covariance_and_contravariance_of_vectorsne) from Wikipedia, but especially the example of a nonorthogonal coordinate system for a tetrahedron. Removing each vector and replacing it with the normal (“the desired orthogonal vector”) at the remaining surface yields a second coordinate system, a complementary one. In other words, we can build up a system “bottom up” by adding dimensions (lines, planes) or we can start with the entire system and work “top down” by removing dimensions, yielding a sequence of hyperplanes. Geometry is what takes place between these two approaches. The coordinate systems are complementary in the way that love supports life. I may not be clear but at least it starts to make sense to me. Also, I started to realize that the natural way to think about both of these coordinate systems is in terms of linear functionals. One set of linear functionals naturally gives rise to a second set of linear functionals. Now the latter turn out to be isomorphic to vectors when we are working in finite dimensions. However, it seems that vectors are Not the natural way to think of this. That’s I think another reason why I was confused. So these are the kinds of matters it would be good to talk with somebody about, especially as regards how they help make sense of the big picture.

premathematics?

I will conclude with a little bit of my own philosophy/metaphysics to show how it can relate to math. It is a structural thinking but is implicit, not explicit as we take “math” to be. I start with the concept of “everything” and note that it has (and is given by) the following four properties:

• Everything has no external context. If you put it in a box, it includes the box. If you think it, then it includes you.
• Everything has no internal structure. It may be orderly, it may be chaotic, it is both, it doesn’t care. Consequently, all statements are true of everything: Everything is hot, everything is cold, everything is good, everything is bad.
• Everything is the simplest possible algorithm. It has no filter: Whatever you think of, you put into everything: the chair, the cup, yourself, God, etc. This means that everything is a universal concept. It’s the same everything, the same algorithm, although we may put different things in it. You may have your name for everything (Universe, being, love, etc.) and I may have mine, but we can talk about the same everything, even though we may have different things to say about it.
• Everything is a required concept. Pragmatically, we all have it. We can’t get rid of it. We couldn’t have learned it from the world, because everything that we know in the world is bounded whereas everything is unbounded. So we must have already had it.

So the concept of “everything” provides an anchor for absolute truth, a preverbal concept that we can think about (as I have above) without necessarily relying on words. In math we have an impulse to talk about “the set of all sets” and “everything” is similar but more basic, without any particular baggage (like sets) because everything is taken as the starting point. In math, I think a better way to think about “everything” is “the state of contradiction” in which all statements are true. The idea is that starting with the state of contradiction, then that state can work backwards to establish the conditions where a noncontradictory system is possible.

Starting with everything as an anchor, it is possible to divide everything into perspectives. It turns out that my imagination is quite limited in doing so. As a freshman in college in 1982-1983 I noticed the following divisions of everything:

• Dividing everything into two perspectives yields a framework for issues of existence. There is one perspective where opposites coexist, as with free will, so that we can consider the question, whether this chair exists or not? And there is another perspective where all things are the same, as with fate, so that we have an answer: if it exists, then it exists, and if not, then not.
• Dividing everything into three perspectives yields a framework for participation, as with the scientific method: we take a stand, follow through and reflect, and then can take a stand again…
• Dividing everything into four perspectives yields a framework for knowledge, four levels: whether, what, how, why.

In math, starting with a state of contradiction, we can imagine it dividing itself into two perspectives to yield a proof by contradiction: if A, then A (all things are the same) but if Not A, then A anyways (opposites coexist). Goedel’s theorem shows that a state of contradiction can yield a division into three perspectives: completeness, consistency and self-reflectivity. The division into four is at work in Yates Index Theorem in Recursive function theory where a level in the jump hierarchy knows everything about the level three jumps below.

The division of everything into five perspectives grounds decision making (time and space). The division of everything into six perspectives grounds morality. Finally, the division of everything into seven perspectives establishes a self-standing logical system. I take this to be Aristotle’s logical square with three sides: All are black, all are white, there exists a black, there exists a white, all are black and there exists a black, all are white and there exists a white, there exists a black and there exists a white. Adding an eighth perspective “all are black and all are white” makes the entire system empty, and it collapses, returning us to the state of contradiction. So this is a good sign for me in the sense that it suggests that the philosophy may be finite and it may truly be possible to know everything.

Finally, I find it very helpful to think in terms of God’s perspective. God can be defined as the division of everything into no perspectives, whereas everything is the division of everything into one perspective. God thus would be that initial state of contradiction from which all is generated. The question which apparently drives God is: Is God necessary? Would God exist even if God didn’t exist? This yields the two perspectives given by the proof by contradiction. So we have God who understands, who makes way for his own nonbeing (the world we find ourselves in), in which God arises even so as one who comes to understand. How do they know they are the same God? Because they understand the same God. So this is a trinity (the well known Father, Son, Spirit of Christianity). But this same “game” also takes place from the Son’s point of view (which requires 8 perspectives) and the Spirit’s point of view (which requires 10 perspectives). And there are 3 more perspectives that permute these 3 structures. So there is a total of 24 = 3 + 8 + 10 + 3 perspectives which are the ways I imagine God and which are a closed system (“God’s dance”) that is the kernel for the more open system that we live in. These questions are the most important ones for me. But I want to show that this kind of thinking provides useful insights for math, physics and all of life.