nLab Lie n-groupoid
Contents
Idea
The geometric infinity-stacks within all smooth infinity-groupoids are called Lie -groupoids. These are equivalently those smooth -groupoids which have a presentation by Kan-fibrant simplicial manifolds. See there for more.
In the language of groupoids, the Kan conditions (see below) correspond to composing and inverting various morphisms. For example, the existence of a composition for arrows is given by the condition , whereas the composition of an arrow with the inverse of another is given by and :
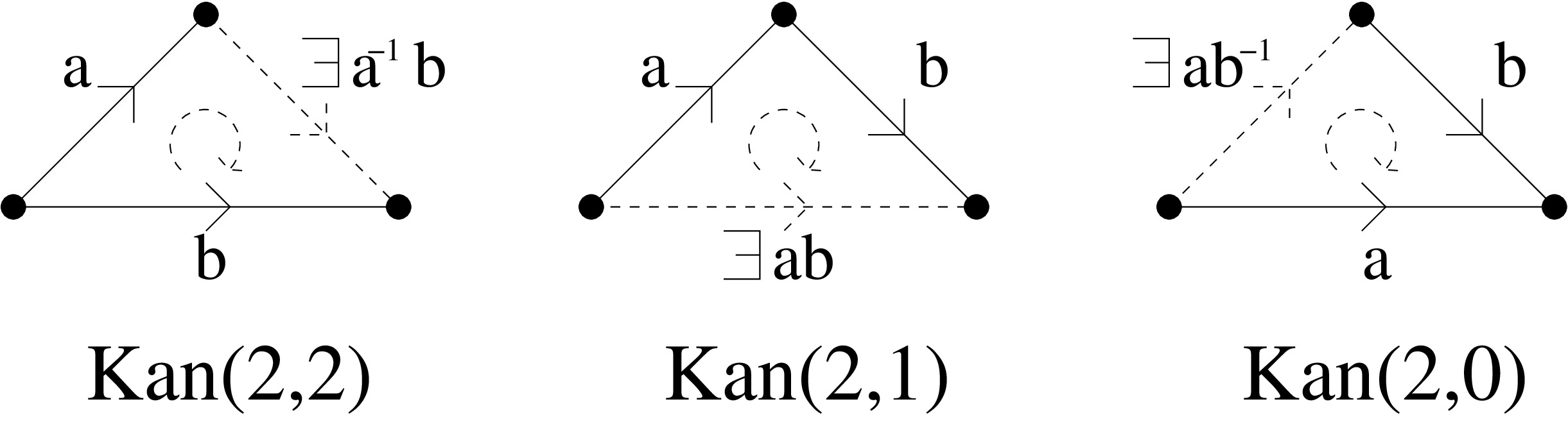
Here we recall that a simplicial set is Kan if any map from the horn to (, ), extends to a map from . Let us call the Kan condition for the horn . A Kan simplicial set is therefore a simplicial set satisfying for all and .
Note that the composition of two arrows is in general not unique, but any two of them can be joined by a -morphism given by .
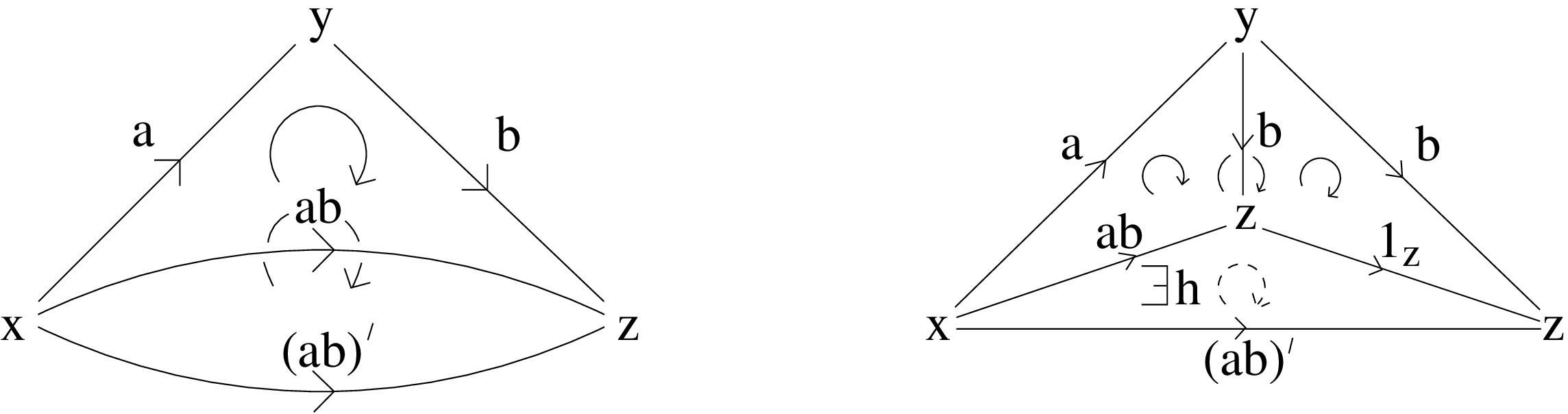
The associativity can be given by and illustrated below:
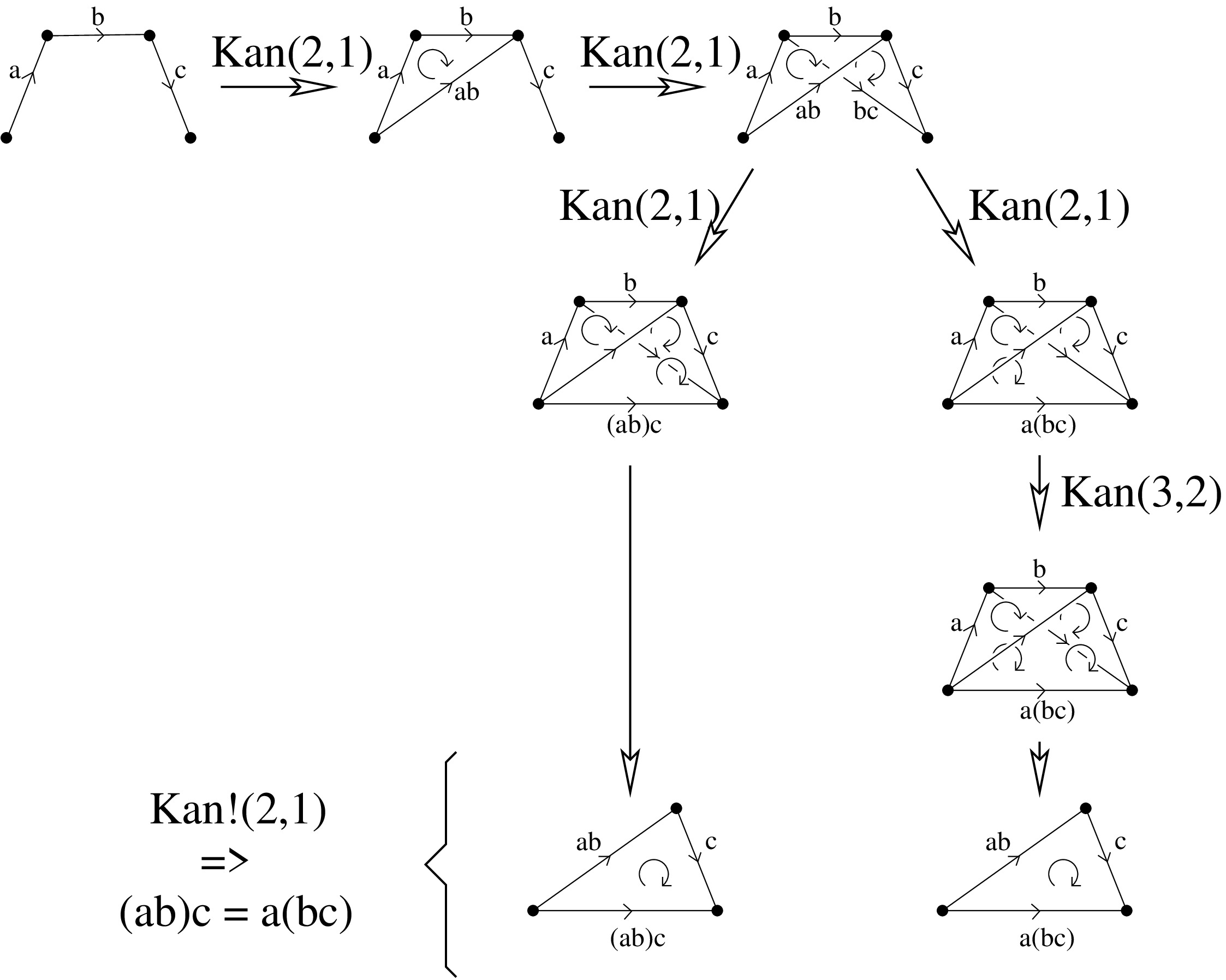
In an -groupoid, the only well-defined composition law is the one for -morphisms. This motivates the following definition.
Definition
An -groupoid () is a simplicial set that satisfies for all and for all , where
: Any map extends to a map .
: Any map extends to a unique map .
Related Lab entries
Last revised on April 21, 2024 at 13:16:03. See the history of this page for a list of all contributions to it.