nLab Mandelbrot set

Idea

The Mandelbrot set is the subset of the complex plane on those points $c \in \mathbb{C}$ on which the iteration of the operation “square and add $c$” does not diverge.

This is a famous example of a fractal.

Definition

For $c \in \mathbb{C}$ a complex number, consider the function on the complex plane that squares its argument and adds $c$ to the result:

$$\array{ \mathbb{C} &\overset{\phantom{AA}f_c\phantom{AA}}{\longrightarrow}& \mathbb{C} \\ z &\overset{\phantom{AA}\phantom{AA}}{\mapsto}& z^2 + c } \,.$$

For $n \in \mathbb{N}$ write

$$f_c^n \coloneqq \underset{n\,\text{factors}}{\underbrace{ f \circ \cdots \circ f \circ f }}$$

for the $n$-fold composition of $f_c$ with itself ($f_c^0 \coloneqq id_{\mathbb{C}}$).

Starting with value $0 \in \mathbb{C}$, this defines a sequence of points in the complex plane $(f_c^n(0))_{i \in \mathbb{C}}$ for each complex number $c \in \mathbb{C}$.

The Mandelbrot set $Mdlbrt \subset \mathcal{C}$ is the subset of the complex plane on those values of $c$ for which the corresponding sequence $(f_c^n)_{n \in \mathbb{B}}$ is bounded

$$Mdlbrt \coloneqq \left\{ c \in \mathbb{C} \;\colon\; (f_c^n(0))_{n \in \mathbb{N}}\, \text{is bounded} \right\} \;\subset\; \mathbb{C} \,.$$

Globally, at low resolution, the Mandelbrot set looks like this:

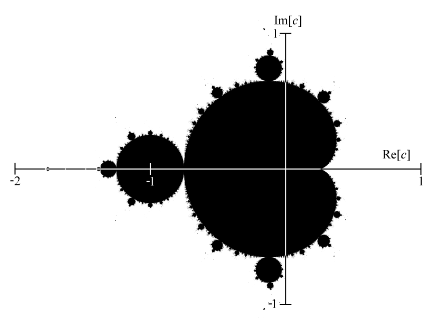
Properties

Topological properties

Definition

(Mandelbrot space)

Regard the Mandelbrot set as a topological space

$$(Mdlbrt, \tau_{sub})$$

via the subspace topology $\tau_{sub}$ inherited from the Euclidean metric topology of $\mathbb{C} \simeq \mathbb{R}^2$.

Proposition

The Mandelbrot space $(Mdlbrot, \tau_{sub})$ (def. ) is a compact topological space.

We prove this below, after the following lemma:

Lemma

(escape radius)

For ${\vert c\vert} \gt 2$ then the sequence $(f_c^n(0))_{n \in \mathbb{N}}$ is not bounded, hence the sequence of absolute values $( {\vert f_c^n(0)\vert} )_{n \in \mathbb{N}}$ diverges for ${\vert c \vert} \gt 2$.

In fact in this case the absolute values increase monotonically:

If ${\vert c\vert} \gt 2$ then for all $n \gt 0$ we have

$${\vert f_c^{n+1}(0)\vert } \gt {\vert f_c^n(0)\vert} \,.$$

Proof

So assume ${\vert c \vert} \gt 2$.

We prove the last statement by induction.

Observe that it is true for $n = 1$, where we have

$$\begin{aligned} {\vert f_c^2(0) \vert} & = {\vert c^2 + c \vert } \\ & \geq {\vert c^2\vert } - {\vert c \vert } \\ & = {\vert c\vert}\underset{\gt 1}{\underbrace{({\vert c\vert}-1)}} \\ & \gt {\vert c\vert } \\ & = {\vert f_c(0) \vert } \end{aligned} \,.$$

Now assume that there is $n \in \mathbb{N}$ such that ${\vert f_c^n(0) \vert} \gt {\vert c\vert}$. Then it follows that

$$\begin{aligned} \frac{ {\vert f_c^{n+1}(0)\vert} }{ \vert f_c^n(0) \vert } & = \frac{ {\vert (f_c^n(0))^2 + c \vert} }{ f_c^n(0) } \\ & \geq \frac{ {\vert f_c^n(0)\vert}^2 - {\vert c \vert} }{ {\vert f_c^n(0)\vert} } \\ & = {\vert f_c^n(0) \vert} - \frac{ {\vert c \vert} }{ {\vert f_c^n(0) \vert} } \\ & \gt \vert c \vert - 1 \\ & \gt 1 \end{aligned} \,.$$

Here the first inequality is due to the triangle inequality, the second is due to the induction assumption, and the last one is due to the initial assumption that ${\vert c \vert} \gt 2$.

Proof

that the Mandelbrot space is compact (prop. )

By lemma the Mandelbrot set is a bounded subset of 2d Euclidean space. Hence by the Heine-Borel theorem is is now sufficient to show that it is a closed subset, this will imply that it is compact.

The subset is closed if for every point $c \in \mathbb{C} \backslash Mdlbrt$ not contained in the Mandelbrot set there is an open neighbourhood of $c$ which still does not intersect the Mandelbrot set.

Now that $c \notin Mdlbrt \subset \mathbb{R}^2$ means by definition that for every positive real number $r$ there is an $n \in \mathbb{N}$ such that $\vert f_c^n(0)\vert \gt r$.

Pick such an $n$ for $r = 2$. Let then

$$\epsilon \coloneqq {\vert f_c^n(0) \vert} - 2 \,.$$

and consider the subset

$$U_{c,n} \coloneqq \left\{ z \in \mathbb{C} \;\vert\; \left( \left({\vert f_c^n(0) \vert} - \epsilon \right) \lt \left( {\vert z\vert} \lt {\vert f_c^n(0) \vert} + \epsilon \right) \right) \right\} \,.$$

This is clearly an open neighbourhood of $f_c^n(0)$. Hence by continuity of the function $f_c^n \colon \mathbb{C} \to \mathbb{C}$, the pre-image

$$(f_c^{n-1})^{-1}(U_{c,n})$$

is an open neighbourhood of $c \in \mathbb{C}$, and by lemma this does not intersect the Mandelbrot set.

Related concepts

• Julia set