nLab experimental alternative definition of functor

Good news! The twists and turns on this page have culminated in Functors and generalized elements. From there, I drew the diagram

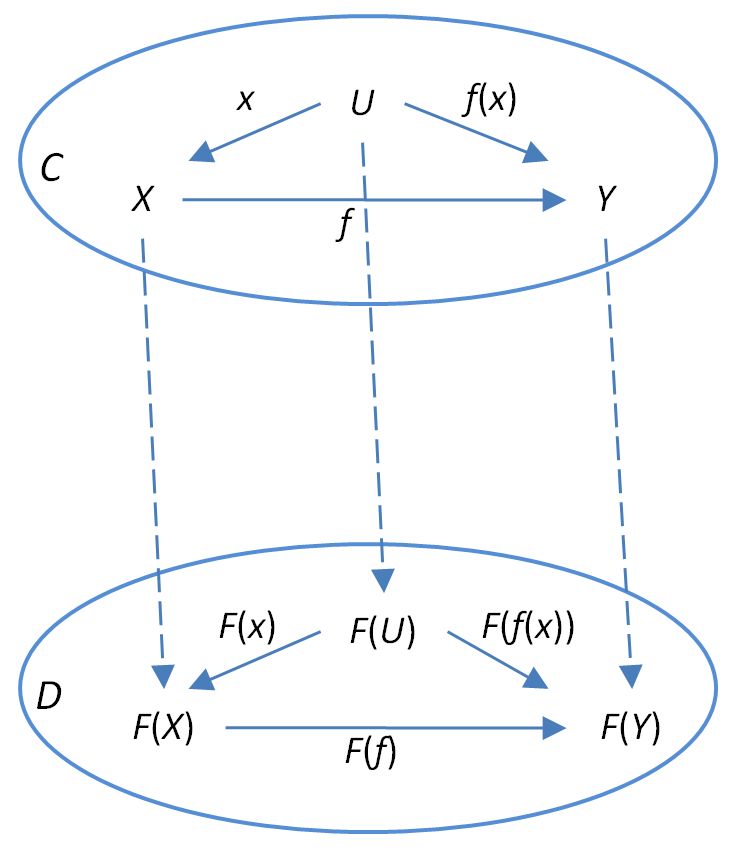
Staring at this diagram resulted in the following:

---

Definition

Given categories $C$ and $D$, a functor $F:C\to D$ is a map that sends each object $x$ in $C$ to an object $F(x)$ in $D$ and each morphism $f:x\to y$ in $C$ to a morphism $F(f):F(x)\to F(y)$ in $D$ such that each commuting diagram in $C$ maps to a commuting diagram in $D$.

---

This has now been included in the definition of functor.

Note this is still essentially the same thing as conveyed in my earlier picture

requiring the square commutes, but is done in a way that avoids introducing the non-standard morphism-like components $\alpha_x:x\to F(x)$.

In other words, if we stopped worrying about what $\alpha_x:x\to F(x)$ really was and simply accepted that the indicated square commutes, it implies automatically that any commuting diagram in $A$ maps to a commuting diagram in $B$.

Contents

This page is an informal/speculative discussion of an alternative (yet hopefully equivalent) definition of functor. It first appeared as a discussion at functor itself, but was subsequently moved here.

Discussion 3.0

I think I may have found a way to express this idea without resorting to non-standard morphism-like maps $x\to F(x)$ or cographs.

Definition

Given categories $A$ and $B$, a map $F:A\to B$ is a functor if for every morphism $f:x\to y$ in $A$

$$F(f) F(x) = F(f(x)).$$

Let’s check…

$$\array{ F(g\circ f) F(x) &= F(g\circ f(x)) \\ &= F(g)\circ F(f(x)) \\ &= F(g)\circ F(f) F(x).}$$

Since this is true for all morphisms $f:x\to y$ and $g:y\to z$, we have

$$F(g)\circ F(f) = F(g\circ f)$$

as required.

Next,

$$F(1_A) F(x) = F(1_A(x)) = F(x)$$

as required.

Therefore, it seems to work.

Note this is still essentially the same thing as conveyed in my earlier picture

requiring the square commutes, but is done in a way that avoids introducing the non-standard morphism-like components.

Discussion 2.0

After Discussion 1.0 below, it seems that the original intention of this page was to define a functor in terms of a cograph. Given a functor, it is straightforward to construct its cograph. However, it may be possible to do the reverse, i.e. start with a cograph and infer the functor that gives rise to that cograph.

Is it possible to define a functor in terms of cograph? If so, how?

Discussion 1.0

Definition

Given small categories $A$ and $B$ define their disjoint union $A\sqcup B$ to be the category with

$$Obj(A\sqcup B) = Obj(A)\sqcup Obj(B)$$

and

$$Hom_{A\sqcup B}(x,y) = \left\{ \begin{aligned} Hom_A(x,y) & if x,y \in A \\ Hom_B(x,y) & if x,y \in B \\ \emptyset & otherwise \end{aligned} \right.$$

There are two inclusion maps

$$i_A:A\to A\sqcup B\quad\text{and}\quad i_B:B\to A\sqcup B$$

defined for any morphism $f:a\to b$ in $A$ and morphism $g:c\to d$ in $B$ by

$$i_A(a) = a\sqcup\emptyset,\quad i_A(b) = b\sqcup\emptyset,\quad\text{and}\quad i_A(f) = f\sqcup\emptyset$$

and

$$i_B(c) = \emptyset\sqcup\c,\quad i_B(d) = \emptyset\sqcup d,\quad\text{and}\quad i_B(g) = \emptyset\sqcup g.$$

Definition

Given categories $A$, $B$ and inclusion maps $i_A:A\to A\sqcup B$, $i_B:B\to A\sqcup B$, a functor is a map $F:A\to B$ together with component morphisms $\alpha_x:i_A(x)\to i_B\circ F(x)$ and $\alpha_y:i_A(y)\to i_B\circ F(y)$ for any morphism $f:x\to y$ in $A$ such that the following diagram commutes:

$$\array{ i_A(x) & \stackrel{i_A(f)}{\to} & i_A(y) \\ \mathllap{\scriptsize{\alpha_x}}\downarrow && \downarrow\mathrlap{\scriptsize{\alpha_y}} \\ i_B\circ F(x) & \stackrel{i_B\circ F(f)}{\to} & i_B\circ F(y) }$$

---

Todd: If $A \sqcup B$ means the disjoint union of $A$ and $B$, then there are no morphisms of the form $i_A(x) \to i_B(F(x))$.

Eric: Hi Todd. I saw your comment after I added the figure above. I am probably not expressing myself clearly. I want to get $Obj(A)$ and $Obj(B)$ into the same category while preserving all morphisms and then ADD components $\alpha_x$ and $\alpha_y$. Is that kind of thing allowed?

I think the picture expresses what I’m trying to do, but maybe I’m converting that into the wrong formulas.

Eric: The idea is that by requiring every such square to commute, you automatically get $F(g\circ f) = F(g)\circ F(f)$ and $F(Id_x) = Id_{F(x)}$. Or so I think…

Eric: Not to mention, this looks more like a natural transformation, so a pattern is more apparent.

Todd: What I was saying is that wherever these $\alpha_x$ are supposed to live, it’s can’t be in $A \sqcup B$, because in $A \sqcup B$, there simply are no morphisms of that form.

Your picture suggests that you have in mind some category $C$ into which $A$ and $B$ embed; it can’t be $A \sqcup B$ since your $\alpha_x$ simply don’t exist there. But it’s some $C$ in which such morphisms $\alpha_x$ exist, let’s say. Then it looks like your notion of functor involves the following things:

• Embeddings (full embeddings?) $i_A: A \to C$, $i_B: B \to C$ into some category $C$.

• A rule which assigns to each object $x$ of $A$ an object $F(x)$ of $B$, and to each morphism $f: x \to y$ of $A$ a morphism $F(f): F(x) \to F(y)$ of $B$. In other words, a map $F: A \to B$ between the underlying directed graphs of $A$ and $B$.

• A rule which assigns to each object $x$ of $A$ a morphism $\alpha_x: i_A(x) \to i_B(F(x)$, making that square commute.

Okay, so far these conditions don’t ensure functoriality: that $F(g \circ f) = F(g) \circ F(f)$ and $F(1_x) = 1_{F(x)}$. You’re going to have to add more conditions to make that inference. For example, suppose $C$ has just one morphism from each object $i_A(a)$ to each object of $i_B(b)$. Then commutativity of those squares is automatic, for any directed graph morphism $F: A \to B$. Insofar as not all graph morphisms are functorial, you can’t infer functoriality.

You could ask that all the $\alpha_x$ be isomorphisms. Then commutativity plus that condition would give functoriality, and your concept amounts to that of ordinary functor $F$ together with an ordinary natural isomorphism $i_A \overset{\sim}{\to} i_B \circ F$.

But the trouble with all this is that I have no idea what $C$ is supposed to be! It can’t be $A \sqcup B$. Would it be something constructed in terms of $A$ and $B$ (and if so, what)? If it’s just any old category into which $A$ and $B$ embed and for which such isos $\alpha_x$ exist (and compatible with the $F(f)$ via commutative diagrams), then I have problems with that too.

Eric; Hi Todd. I think I’m confused because with the standard definition of functor $F:A\to B$ no one ever complains about writing $F(x)\in B$, so in a way, isn’t $F$ an arrow from $x\in A$ to $F(x)\in B$? We also write $F(f)\in B$, which makes me think $F$ is a bunch of 1-arrows and 2-arrows. I mean, doesn’t the picture make sense? Why is it so hard to convert the picture to a mathematical statement?

: Toby: Eric, here you seem to be conflating these two arrows: $\to$ and $\mapsto$. At the level of functions between sets, if $A$ and $B$ are sets and $f$ is a function from $A$ to $B$, then I write $f\colon A \to B$ or $A \overset{f}\to B$. Then if $x$ is an element of $A$ and $y$ is an (the) element of $B$ such that $y = f(x)$, then I write $f\colon x \mapsto y$ or $x \overset{f}\mapsto y$. Or without bothering with $y$, I write $f\colon x \mapsto f(x)$ or $x \overset{f}\mapsto f(x)$. (Actually, this is best when ‘$x$’ is a variable and ‘$f(x)$’ is a formula in terms of that variable; for example, if $f$ is the squaring function, then I write $f\colon x \mapsto x^2$ or $x \overset{f}\mapsto x^2$, and this serves to define $f$.)

: Actually, you can find a lot of literature where the same symbol ‘$\rightarrow$’ is used for both $\to$ and $\mapsto$, but they are still different concepts.

: Of course, what the cograph gets you is that it turns $\mapsto$ into a special case of $\to$. But they are still different; $f\colon A \to B$ is an arrow in the category of sets or (in the categorified case) in the $2$-category of categories, while $x \overset{f}\mapsto y$ is (only in the categorified case) an arrow in the cograph of $f$.

Eric: Hmm.. but we ARE talking about cographs :) At least I was accidentally :)

Urs Schreiber: concerning the nature of $C$: as I suggested before, it does make sense to take this to be the cograph of a functor. And indeed, in some situations it is useful to define the notion of functor in terms of the notion of cograph. In Higher Topos Theory the notion of adjoint (infinity,1)-functor is defined entirely in terms of cographs of functors.

Eric: Thanks Urs. Now I just need to parse what you say into something I can understand, but it is encouraging. In fact, quoting myself from earlier in the discussion:

It seems like maybe I am trying to work backwards, i.e. define a functor via a cograph.

When I tried to grok “cograph” on my personal web Natural Transformation, I stripped out the line including the functor and with Toby’s help, realized what I (think I) was talking about was the disjoint union of categories.

I guess, my plan of attack now is to see how we can define functor via cograph. For some reason, that makes sense to me.

Todd: Yes, that’s true, the cograph is fine. I thought that Eric had wanted a $C$ which would uniformly work, independently of which functor $F$ was being considered. Instead, we construct the cograph $C$ in terms of $F$, and everything is for the best in this best of all possible worlds. And we get the picture Eric was aiming for.

Eric: Neat. Now, if we (I’ll try, but I’m not confident and wouldn’t mind if someone else did it!) can write down a succinct definition of functor in terms of cographs with a picture like the one above (if not that one), we could add it to functor.

Eric: By the way, here is something I wrote on my personal web Natural Transformation:

Urs Schreiber: at cograph it is indicated how that concept encodes the notion of profunctor which is a bit more general than that of functor.

Eric: Oh! That is pretty! Thanks. I like this diagram

\array{

R &\to& {*}
\\
\downarrow && \downarrow
\\
X \times Y &\stackrel{\chi_R}{\to}& \{0,1\}

}

>I need to think about it, but a vale of fog has been lifted. More fog remains, but thanks! *** ###Definition### Given small categories $A$ and $B$ define their **disjoint union** $A\sqcup B$ to be the category with $$Obj(A\sqcup B) = Obj(A)\sqcup Obj(B)

and

$$>I need to think about it, but a vale of fog has been lifted. More fog remains, but thanks! *** ###Definition### Given small categories$$

There are two inclusion maps

$$i_A:A\to A\sqcup B\quad\text{and}\quad i_B:B\to A\sqcup B$$

defined for any morphism $f:a\to b$ in $A$ and morphism $g:c\to d$ in $B$ by

$$i_A(a) = a\sqcup\emptyset,\quad i_A(b) = b\sqcup\emptyset,\quad\text{and}\quad i_A(f) = f\sqcup\emptyset$$

and

$$i_B(c) = \emptyset\sqcup\c,\quad i_B(d) = \emptyset\sqcup d,\quad\text{and}\quad i_B(g) = \emptyset\sqcup g.$$

---

I intentionally did not use the word “functor” above even though that is really the coproduct in Cat. The reason is that I want to use this disjoint union to define a functor. The following is a possible starting point:

Definition

Given categories $A$, $B$ and inclusion maps $i_A:A\to A\sqcup B$, $i_B:B\to A\sqcup B$, a functor is a map $F:A\to B$ that assigns morphisms $\alpha_x:i_A(x)\to i_B\circ F(x)$ and $\alpha_y:i_A(y)\to i_B\circ F(y)$ for any morphism $f:x\to y$ in $A$ such that the following diagram commutes:

$$\array{ i_A(x) & \stackrel{i_A(f)}{\to} & i_A(y) \\ \mathllap{\scriptsize{\alpha_x}}\downarrow && \downarrow\mathrlap{\scriptsize{\alpha_y}} \\ i_B\circ F(x) & \stackrel{i_B\circ F(f)}{\to} & i_B\circ F(y) }$$

---

Discussion

Eric: Motivated by some discussion over at natural transformation, I was wondering if the following alternative definition of functor holds water:

Definition

Given categories $A$, $B$, a functor is a map $F:A\to B$ that assigns maps $\alpha_x:x\to F(x)$ and $\alpha_y:y\to F(y)$ for any morphism $f:x\to y$ in $A$ such that the following diagram commutes:

\array{

x
& 
\stackrel{f}{\to} 
& 
y 
\\ 
\mathllap{\scriptsize{\alpha_x}}\downarrow 
&& 
\downarrow\mathrlap{\scriptsize{\alpha_y}} 
\\ F(x) 
& 
\stackrel{F(f)}{\to} & F(y) 

}

$$If so, it has a certain beauty that appeals to me. Thanks! Urs: that diagram seems to be meaningful only if$$

\array{ i_A(x) & \stackrel{i_A(f)}{\to} & i_A(y) \ \mathllap{\scriptsize{\alpha_x}}\downarrow && \downarrow\mathrlap{\scriptsize{\alpha_y}} \ i_B\circ F(x) & \stackrel{i_B\circ F(f)}{\to} & i_B\circ F(y) }

$$It follows that$$