nLab
manifold

Idea

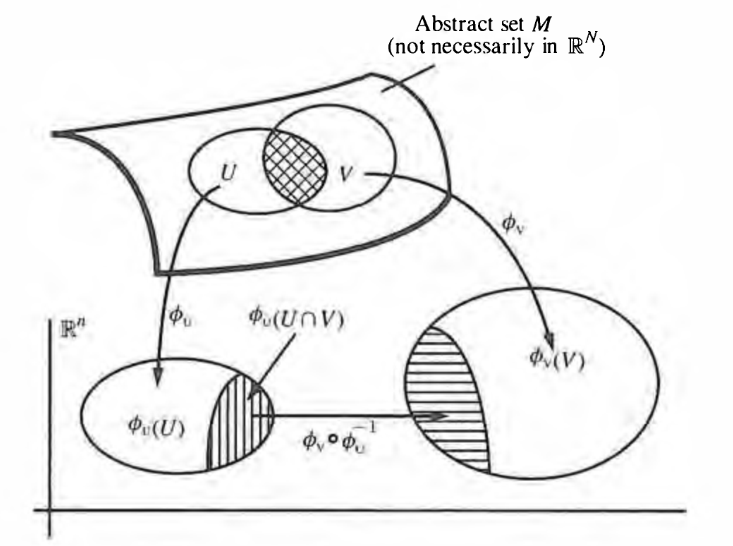
A manifold is a topological space which looks locally like a Cartesian space, commonly a finite-dimensional Cartesian space ${ℝ}^n$ but possibily an infinite-dimensional topological vector space-

What “locally looks like” means depends on what sort of structure we are considering a Cartesian space to embody. At one extreme, we can think of ${ℝ}^n$ as merely a topological space. Or, ${ℝ}^n$ may be considered as carrying more rigid types of structure, such as $C^k$-differential structure, smooth structure, piecewise-linear (PL) structure, real analytic structure, affine structure, hyperbolic structure, foliated structure, etc., etc. Accordingly we have notions of topological manifold, differential manifold, smooth manifold, etc. By default these are modeled on finite dimensional spaces, but most notions have generalizations to a corresponding notion of infinite dimensional manifold.

In any case, the type of geometry embodied in a particular flavor of manifold is controlled by a particular groupoid of transformations which preserves whatever geometric features one is interested in; cf. Felix Klein’s Erlanger Programm.

Definitions

To give a reasonably general notion of manifold, we first specify the kinds of concrete geometric groupoids which come into play.

Pseudogroups

Definition

A pseudogroup on a topological space (or locale) $X$ is a groupoid $G$ each of whose objects is an open subset of $X$, and whose morphisms are homeomorphisms between such open sets, satisfying the following conditions:

• The objects cover $X$. (Equivalently, in light of the last axiom, every open set of $X$ is an object of $G$.)
• If $g:V\to W$ belongs to $G$ and $U\subseteq V$ is an open set, then the restriction $g{\mid }_U:U\to g(U)$ belongs to $G$. (Equivalently, in light of the other axioms, every inclusion map $\mathrm{id}{\mid }_U:U\to V$ belongs to $G$.)
• (sheaf property) If $g:U\to V$ is a homeomorphism and if there is a covering $U_{\alpha }$ of $U$ such that the restrictions $g{\mid }_{U_{\alpha }}:U_{\alpha }\to g(U_{\alpha })$ are morphisms of $G$, then $g$ is also morphism of $G$.

Example

Commonly used choices for $X$ in def. 1 include

• the Cartesian space ${ℝ}^n$ (for real manifolds)

• the complex plane ${ℂ}^n$ (for complex manifolds)

• the half-space $$H^n=\{(x_1,\dots ,x_n)\in {ℝ}^n:x_1\ge 0\}$$ (for manifolds with boundary)

• the $n$-cube $I^n=[0,1{]}^n$.

For the sake of concreteness, the reader may as well focus on the case $X={ℝ}^n$.

Charts

Let $G$ be a pseudogroup on $X$.

Definition

A $G$-chart on a topological space $M$ is an open subset $U$ of $M$ together with an embedding

$$\varphi :U\to X.$$\phi: U \to X\,.

Two charts $\varphi :U\to X$ and $\psi :V\to X$ are compatible if

$$\psi \circ {\varphi }^{-1}:\varphi (U\cap V)\to \psi (U\cap V)$$\psi \circ \phi^{-1}: \phi(U \cap V) \to \psi(U \cap V)

belongs to $G$.

Definition

A $G$-atlas on a topological space $M$ is a family of compatible charts $({\varphi }_{\alpha }:U_{\alpha }\to X{)}_{\alpha }$, def. 2, such that $(U_{\alpha }{)}_{\alpha }{)}_{\alpha }$ covers $M$. The (restricted) maps ${\varphi }_{\alpha \beta }={\varphi }_{\beta }\circ {\varphi }_{\alpha }^{-1}$ are called transition functions between the charts of the atlas.

Manifolds

Definition

A $G$-manifold is a topological space equipped with a $G$-atlas, def. 3.

Remark

This means that we can think of a $G$-manifold as a space which is locally modeled on $X$ according to the geometry $G$.

Remark

It is almost invariably the case in classical manifold theory that one requires some technical niceness properties on the topological space underlying a manifold.

Usually, in the definition of manifold it is understood that the underlying topological space

1. is a Hausdorff topological space (if not one usually speaks explicitly of a non-Hausdorff manifold)

2. is a paracompact topological space;

Often it is also assumeed that the topology has a countable basis as well.

In the typical cases mentioned above for $X$, this will mean that $M$ is metrizable. In many studies, for example in cobordism theory, one goes even further and assumes the manifolds are compact.

Remark

An atlas is not considered an essential part of the structure of a manifold: two different atlases may yield the same manifold structure. This is encoded by the following definition 5 of isomorphisms between manifolds.

Isomorphism of manifolds

Definition

An isomorphism of $G$-manifolds $f:M\to N$ (defined by chosen atlas structures, def. 3) is a homeomorphism $f$ such that

$$\varphi (U\cap f^{-1}(V))\stackrel{{\varphi }^{-1}}{\to }U\cap f^{-1}(V)\stackrel{f}{\to }f(U)\cap V\stackrel{\psi }{\to }\psi (f(U)\cap V)$$\phi(U \cap f^{-1}(V)) \overset{\phi^{-1}}{\to} U \cap f^{-1}(V) \overset{f}{\to} f(U) \cap V \overset{\psi}{\to} \psi(f(U) \cap V)

is in $G$ whenever $(U,\varphi )$ is a coordinate chart, def. 2 of $x\in M$, and $(V,\psi )$ is a coordinate chart of $f(x)\in N$.

If $M_1$ and $M_2$ are two $G$-manifold structures on the same topological space $M$, then $M_1$ and $M_2$ are considered equal as $G$-manifolds if $\mathrm{id}:M\to M$ is an isomorphism from $M_1$ to $M_2$ (and hence also from $M_2$ to $M_1$).

Alternatively, atlases are ordered by inclusion, and two atlases define the same manifold structure on $M$ if they have a common upper bound. Equivalently, two atlases define the same manifold structure if each chart of one is compatible with each chart of the other. Or, one could extend any atlas to the (unique) maximal atlas containing it, which consists of all charts compatible with each of the charts in the original atlas, and simply identify a manifold structure with a maximal atlas.

Rafael: Can one define a manifold object in a category C as a G-manifold with G related to C? What would the relation between G and C be to obtain G-manifolds in C as manifold objects?

Toby: Yes, I think that this would make perfect sense; I think that we'd want $G$ to be an internal groupoid in $C$. Note that defining things like ‘smooth manifold’ in $C$ might still be difficult, but we've reduced it to internalising Cart Sp in $C$. (There's also the matter that the above definition takes a notion of space for granted, so you'd have to internalise that into $C$ too, but I'm not sure how important that really is, when I think about how the topology on a smooth manifold can be recovered from the smooth structure.)

Rafael: Can someone that knows more than me about this add the result of this question to this article so nobody have to ask again.

Toby: I'd rather not, since it's all ‘I think’ and ‘might be difficult’; it's better as a query box, moved to the bottom if necessary. But if Todd agrees with me, then maybe he'll add it.

Morphisms of Manifolds

Note: the following is tentative “original research”. It is prompted by the desire to extend the pseudogroup approach for defining general notions of manifold, so as to cover also an appropriate general notion of “map”. Comments, improvements, and corrections are encouraged – Todd.

I've read through it once, and it makes sense. I'll read through it again more carefully later. —Toby

We begin by defining the 2-poset (i.e., locally preordered bicategory) of regions, denoted $\mathrm{Reg}$. The objects are topological spaces (or locales if you prefer); the morphisms are partial functions with open domain, that is spans

$$X\stackrel{i}{\leftarrow }U\stackrel{f}{\to }Y$$X \overset{i}{\leftarrow} U \overset{f}{\to} Y

where $f$ is continuous and $i$ is an open embedding. The spans are locally (that is, for fixed $X$ and $Y$) ordered by inclusion.

These local posets are not cocomplete, but they admit certain obvious joins: given a family of regional maps

$$(U_{\alpha },f_{\alpha }):X\to Y$$(U_\alpha, f_\alpha): X \to Y

the join ${\bigvee }_{\alpha }(U_{\alpha },f_{\alpha })$ exists iff we have local compatibility:

$$f_{\alpha }{\mid }_{U_{\alpha }\cap U_{\beta }}=f_{\beta }{\mid }_{U_{\alpha }\cap U_{\beta }}$$f_{\alpha}|_{U_\alpha \cap U_\beta} = f_{\beta}|_{U_\alpha \cap U_\beta}

for all $\alpha ,\beta$. Notice that composition on either side with a $1$-cell preserves any local joins which exist.

Every coreflexive morphism $r\le 1_X$ in $\mathrm{Reg}$ splits: there is a map in $\mathrm{Reg}$,

$$\mathrm{Ext}(r)\stackrel{\mathrm{id}}{\leftarrow }\mathrm{Ext}(r)\stackrel{i}{\to }X,$$Ext(r) \overset{id}{\leftarrow} Ext(r) \overset{i}{\to} X,

whose opposite $i^{\mathrm{op}}:X\to \mathrm{Ext}(r)$ also belongs to $\mathrm{Reg}$ (that is, $i$ is an open embedding), and the equations

$$i^{\mathrm{op}}\circ i=1_{\mathrm{Ext}(r)}i\circ i^{\mathrm{op}}=r$$i^{op} \circ i = 1_{Ext(r)} \qquad i \circ i^{op} = r

hold. The object $\mathrm{Ext}(r)$ may be called the extension of $r$. This splitting is a kind of comprehension principle familiar from the theory of allegories, among other things.

A cartology is a (locally full) subbicategory $i:C\hookrightarrow \mathrm{Reg}$ such that

• (Closure under open subspaces) If $X\in \mathrm{Ob}(C)$ and $r\le 1_X$ in $\mathrm{Reg}$, then $i:\mathrm{Ext}(r)\to X$ and its opposite $i^{\mathrm{op}}$ are morphisms of $C$.
• (“Sheaf condition”) The inclusion $i:C\to \mathrm{Reg}$ reflects and preserves local joins.

Intended examples include the case where the objects of $C$ are Euclidean spaces ${ℝ}^n$, and morphisms are spans

$$(U,f):{ℝ}^m\to {ℝ}^n$$(U, f): \mathbb{R}^m \to \mathbb{R}^n

where $f$ is smooth.

Given a cartology $C$, a morphism $r=(U,f):X\to Y$ in $C$ is pseudo-invertible if there exists $s=(V,g):Y\to X$ such that $s\circ r=1_U$ and $r\circ s=1_V$.

Lemma

In a cartology, the pseudo-invertible morphisms from an object $X$ to itself form a pseudogroup (as defined earlier).

The notion of a $C$-manifold modeled on an object $X$ of $C$ is defined just as before, using the pseudogroup on $X$ implied by the previous lemma. In particular, we have $C$-charts of an atlas structure on $M$, which are morphisms in $\mathrm{Reg}$

$$X\stackrel{i}{\leftarrow }U\stackrel{\varphi }{\to }M$$X \overset{i}{\leftarrow} U \overset{\phi}{\to} M

satisfying the expected properties. We can thus speak of $C$-manifolds (or $(C,X)$-manifolds if we want to make explicit the modeling space $X$).

Now, given a cartology $C$, we define the category of $C$-manifolds. Let $M$ be a $(C,X)$-manifold and $N$ a $(C,Y)$-manifold. Then, a $C$-morphism from $M$ to $N$ is a continuous map $f:M\to N$ such that the $\mathrm{Reg}$-composite

$$\begin{array}{ccccccccccccc}& & U& & & & M& & & & V& & \\ & i\swarrow & & \searrow \varphi & & 1\swarrow & & \searrow f& & \psi \swarrow & & \searrow j& \\ X& & & & M& & & & N& & & & Y\end{array}$$\array{ && U &&&& M &&&& V && \\ & i \swarrow && \searrow \phi && 1 \swarrow && \searrow f && \psi \swarrow && \searrow j & \\ X &&&& M &&&& N &&&& Y }

belongs to $C$, for every pair of charts $(U,\varphi ):X\to M$ and $(V,\psi ):Y\to N$.

These definitions need to be carefully checked against known examples (e.g., the categories $\mathrm{Top}$, $\mathrm{PL}$, and $\mathrm{Smooth}$, among others).

Examples

If the term “manifold” appears without further qualification, what is usually meant is a smooth $n$-manifold of some natural number dimension $n$: a $G$-manifold where $G$ is the pseudogroup of invertible $C^{\mathrm{\infty }}$ maps between open sets of ${ℝ}^n$. Replacing ${ℝ}^n$ here by a half-space $\{x\in {ℝ}^n:x_1\ge 0\}$, one obtains the notion of smooth manifold with boundary. Or, replacing ${ℝ}^n$ here by the $n$-cube $I^n$, one obtains the notion of (smooth) $n$-manifold with (cubical) corners. Morphisms of manifolds are here called smooth maps, and isomorphisms are called diffeomorphisms. (In manifold theory, one usually reserves the term smooth function for smooth maps to $ℝ$.)

A topological $n$-manifold is a manifold with respect to the pseudogroup of homeomorphisms between open sets of ${ℝ}^n$. Any continuous function between topological manifolds is a morphisms, and any homeomorphism is an isomorphism. A piecewise-linear (PL) $n$-manifold is where the pseudogroup consists of piecewise-linear homeomorphisms between such open sets; morphisms are called piecewise-linear (PL) maps.

One can go on to define, in a straighforward way, real analytic manifolds, complex analytic manifolds, elliptic manifolds, hyperbolic manifolds, and so on, using the general notion of pseudogroup.

Any space $X$ can always be turned into a manifold modelled on itself, using any pseudogroup $G$. Simply take the inclusions of open sets as charts.

The tangent Bundle

Many species of manifolds (Riemannian manifold, pseudo-Riemannian manifold, symplectic manifold, and so on) involve extra structures defined on the tangent bundle of a smooth manifold. This is perhaps the most fundamental construction in manifold theory.

If $M$ is a smooth $n$-manifold defined by an atlas $(U_{\alpha },{\varphi }_{\alpha })$, then we may define its tangent bundle $TM$ by a gluing construction in $\mathrm{Top}$, taking $TM$ to be the quotient of the disjoint sum

$$\sum _{\alpha }{U}_{\alpha }\times {ℝ}^n$$\sum_\alpha U_\alpha \times \mathbb{R}^n

obtained by dividing by the equivalence relation

$$(p\in U_{\alpha },v)\sim (p\in U_{\beta },g_{\alpha \beta }(p)v)$$(p \in U_\alpha, v) \sim (p \in U_\beta, g_{\alpha\beta}(p) v)

where $p\in U_{\alpha }\cap U_{\beta }$, and $g_{\alpha \beta }(p)\in \mathrm{GL}({ℝ}^n)$ is the result of differentiating the transition function ${\varphi }_{\alpha \beta }$ at the point ${\varphi }_{\alpha }(p)$. We thus obtain a covering $U_{\alpha }\times {ℝ}^n$ of $TM$, and these form coordinate charts of a smooth manifold structure on $TM$ in a more or less evident way. There is an obvious projection map $\pi :TM\to M$, called the tangent bundle; the fiber ${\pi }^{-1}(p)$ over a point $p\in M$ is called the tangent space at $p$, denoted $T_{p}M$. Elements $v\in T_{p}M$ are called tangent vectors at $p$.

• It is not immediately apparent that this construction yields the same manifold (in the sense described earlier) independent of the atlas chosen. To make this manifest, it is preferable to deal with coordinate-free expressions, defining for example tangent vectors with reference to the sheaf of smooth functions on $M$. We discuss this below.

The functions

$$g_{\alpha \beta }:U_{\alpha }\cap U_{\beta }\to \mathrm{GL}({ℝ}^n)$$g_{\alpha \beta}: U_\alpha \cap U_\beta \to GL(\mathbb{R}^n)

satisfy Čech 1-cocycle relations

$$g_{\alpha \gamma }=g_{\beta \gamma }\circ g_{\alpha \beta }:U_{\alpha }\cap U_{\beta }\cap U_{\gamma }\to \mathrm{GL}({ℝ}^n)$$g_{\alpha \gamma} = g_{\beta\gamma} \circ g_{\alpha\beta}: U_{\alpha} \cap U_\beta \cap U_\gamma \to GL(\mathbb{R}^n)

$$g_{\alpha \alpha }=1:U_{\alpha }\to \mathrm{GL}({ℝ}^n)$$\qquad g_{\alpha\alpha} = 1: U_{\alpha} \to GL(\mathbb{R}^n)

These 1-cocycle data make the tangent bundle an $n$-dimensional vector bundle with structure group $\mathrm{GL}({ℝ}^n)$.

Generalizations

• generalized smooth space

• differentiable stack

• derived smooth manifold

• supermanifold

  • Euclidean supermanifold (notice that the definition of that is very much along the lines of the Klein-program-style definition above).

Related concepts

• low-dimensional topology

• projective manifold

• manifold with boundary

• closed manifold

References

• John Loftin, The real definition of a smooth manifold (pdf)