Eric Forgy diamonation

Diamonation represents a conjecture of mine I’ve thought about for years now. Just as any smooth manifold $M$ can be triangulated, any directed space can be diamonated.

If this conjecture can be proved then it would allow us to extend the results of our paper

• Discrete differential geometry on causal graphs

to any smooth manifold.

Here are some places I’ve discussed diamonation:

• Via Google

More specifically

• The Search for Discrete Differential Geometry
• Measure on Paths
• Canonical Measures on Configuration Spaces
• Spans in Quantum Theory
• Locally Lorentzian Latticization

Illustration

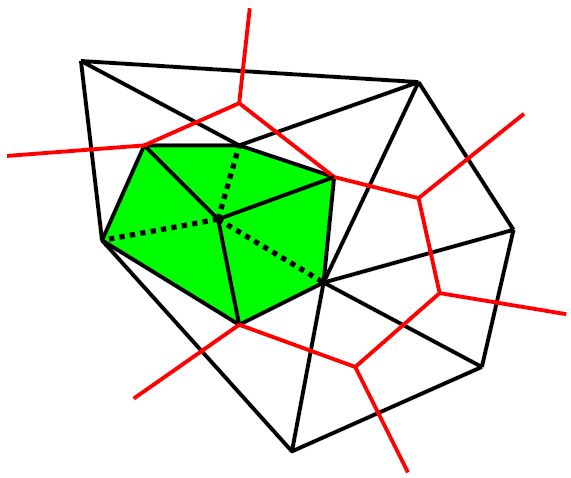
Here is a triangulation and its dual. Note the top-left dual cell has four sides, whereas bottom-right dual cell has six sides.

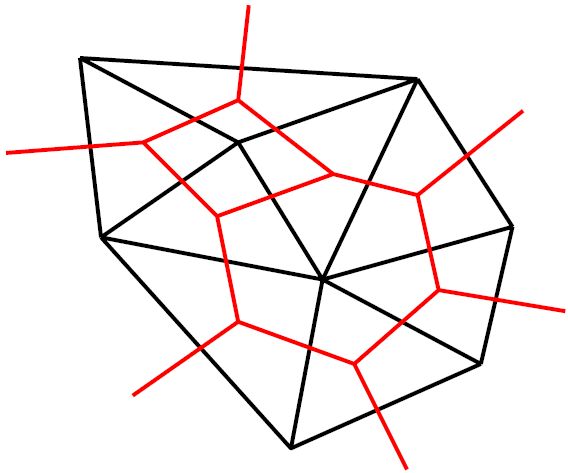
Begin at the center of any triangle, and draw a line to the center of any neighboring dual cell.

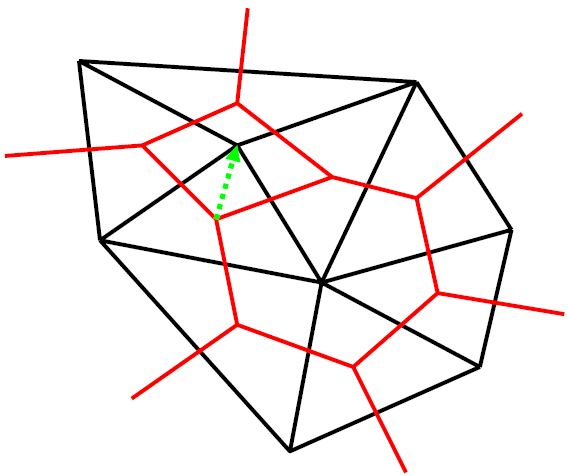
Next, draw a line from that point to either the nearest right (relative to the original node) or nearest left node of the dual cell.

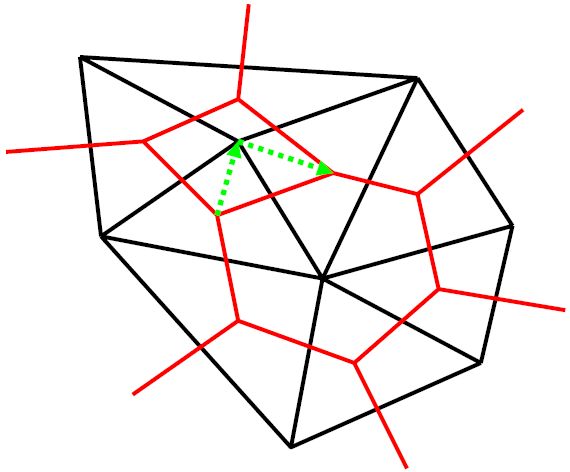
Finally, close the loop resulting in a triangle (as projected along the time direction, which is out of the page).

Beginning at the original node, begin another loop by retracing the same first step as last time.

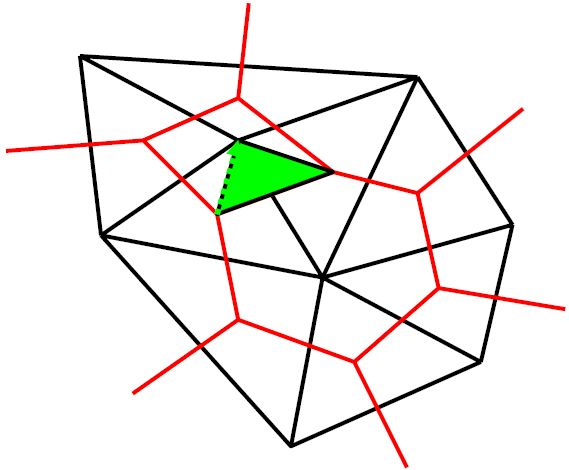
Now turn the other way.

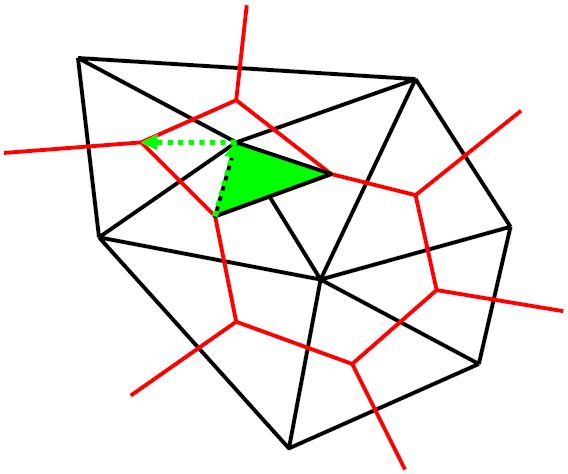
Close the loop.

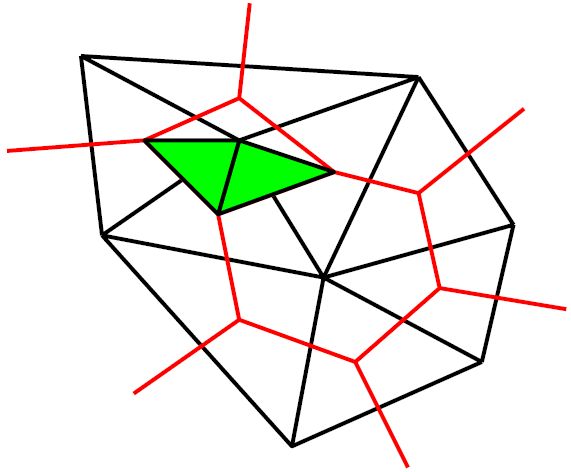
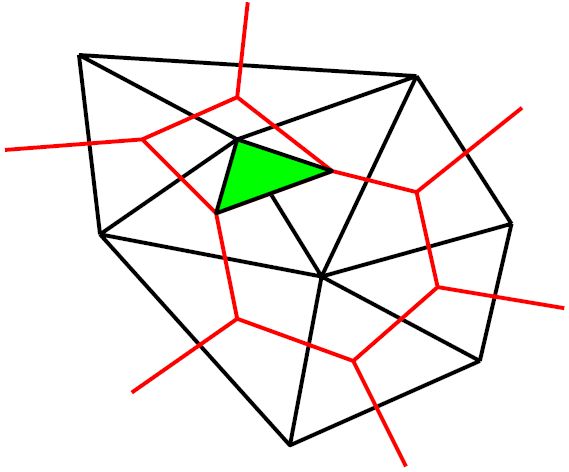
Continue around the original node until you have obtained the configuration below. I claim that we have just bounded a 3-diamond.

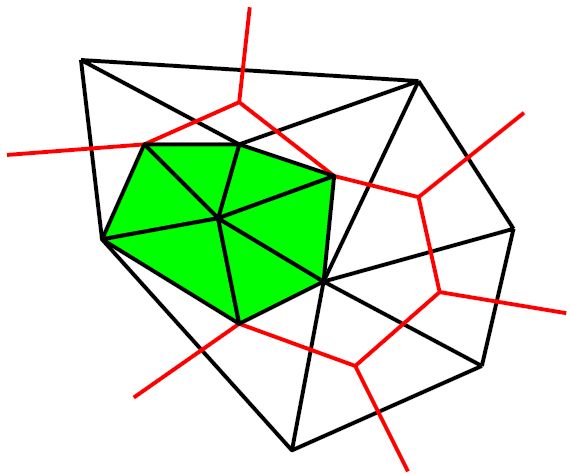
I think this picture makes it more clear that we’ve created a 3-diamond.

Note: “Diamond” is a prettier sounding word for “Directed Cube”, so a 3-diamond is a directed 3-cube.

References

• Jean-Yves Welschinger, Associahedral categories, particles and Morse functor