John Baez Dual Circuit
Network duality
You may know Poincaré duality for graphs drawn on a sphere: you get a new graph from an old one by:
- drawing a new vertex in the middle of each old face,
- replacing each old edge with a new ‘dual edge’ that crosses the old one, and
- drawing a new face centered at each old vertex.
For “closed” planar circuits - those without input and output wires - we can extend this notion to a notion of duality for circuits made of resistors. To do this, we simply carry out the above operations and give each new edge a resistance that’s the inverse of the resitance labelling the old edge.
For circuits with input and output wires, like we’ve got here, we need a generalization: Poincaré duality for graphs drawn on a closed disk! This is should probably be called “Poincaré-Lefschetz duality”.
For more details on how this works, see week295 of This Week’s Finds.
The utility of duality in circuit theory lies in the fact that once a circuit is analyzed, its dual is in essence analyzed for free. Note that if the dual of circuit A is circuit B, then the dual of B is A. Also note that the well-known concepts of ‘series’ and ‘parallel’ are interchanged under duality.
A standard basic reference on linear circuit theory is:
- Leonard S. Bobrow, Elementary Linear Circuit Analysis, 2nd edition, Oxford U. Press, Oxford, 1996.
Examples
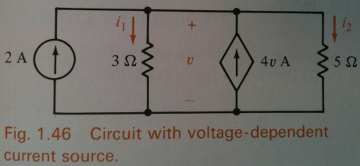
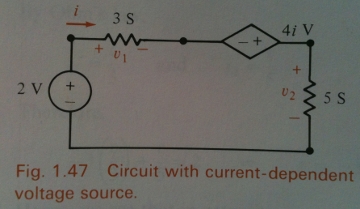
Example. The above circuits are dual to each other. From Bobrow, OUP 1996.

Table summary of the dual circuit rules. From Bobrow, OUP 1996.
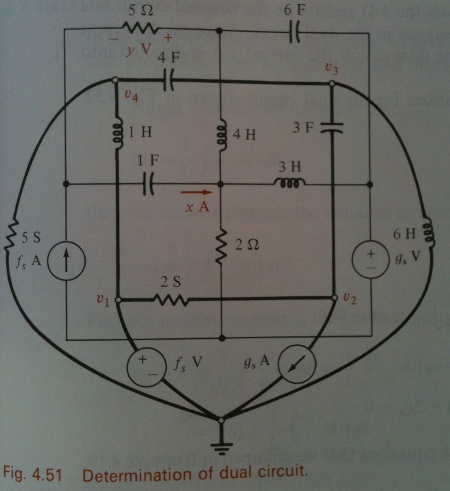
Example. The inner circuit (light lines) and its dual (given as the outer circuit with dark lines). From Bobrow, OUP 1996.
Last revised on January 24, 2011 at 03:01:32. See the history of this page for a list of all contributions to it.