nLab 6j symbol
Contents
Idea
symbols are pieces of combinatorial data which can be associated to fusion categories, encoding their associator with a finite amount of algebraic data. The symbols along with the fusion ring is enough data to uniquely reconstruct the category.
symbols are only defined for multiplicity free fusion categories. That is, fusion categories in which all of the fusion coefficients are or . For fusion categories with larger coefficients, one has to replace symbols (which are complex numbers) with higher-dimensional matrices.
The name “ symbol” comes from the fact that the symbol has indicies associated to it.
The symbols depend on a local choice of basis of hom-spaces of your fusion category, and hence they are not bona-fide invariants. Choosing a different choice of local basis corresponds to a gauge transformation.
Definition
Let be a multiplicity free fusion category. Let
be its associator. We wish to encode the associator with a finite amount of algebraic data. That is, with a finite quantity of complex numbers. We do this by studying the action of with respect to the (finite) set of isomorphism classes of simple objects of .
For every triple of simple objects of , choose a distinguished generator
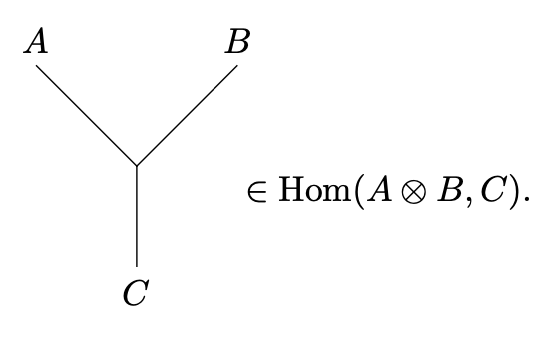
This will be a non-zero morphism whenever and otherwise. Here, we are using the graphical language of string diagrams. There generators are chosen arbitrarily, except for the conditions that
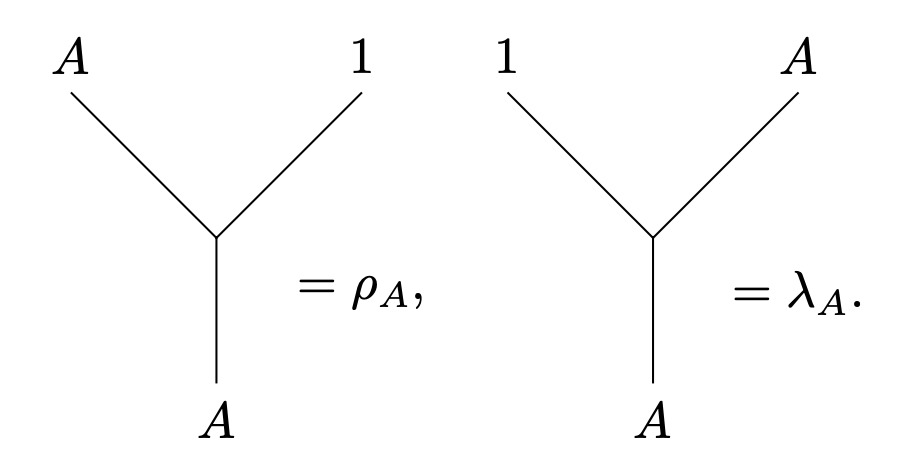
where denotes the right unitor and denotes the left unitor.
Note the key use of the fact that is multiplicity free. If fusion coefficients could be then we would not have one-element bases of the spaces . Instead, we would have to choose larger bases of these spaces are get matrices for our symbols instead of complex numbers.
For all quadruples of simple objects, there is a basis of given by the symbols
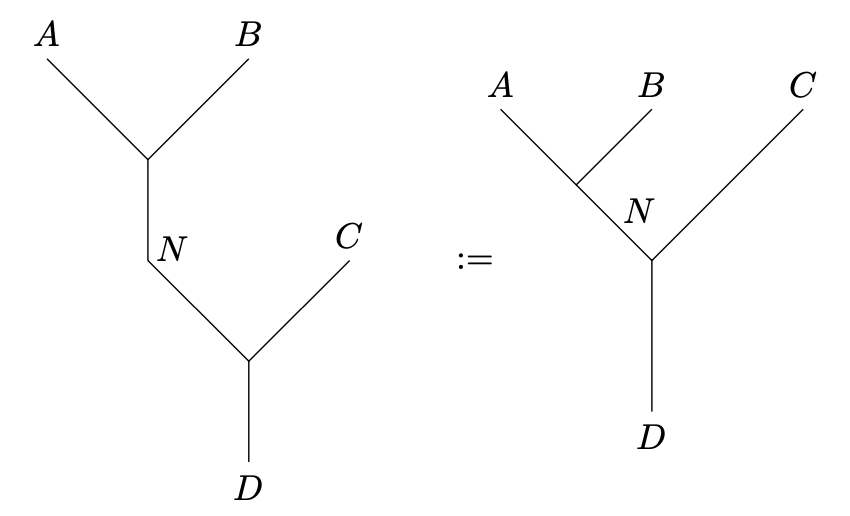
and there is a basis of .
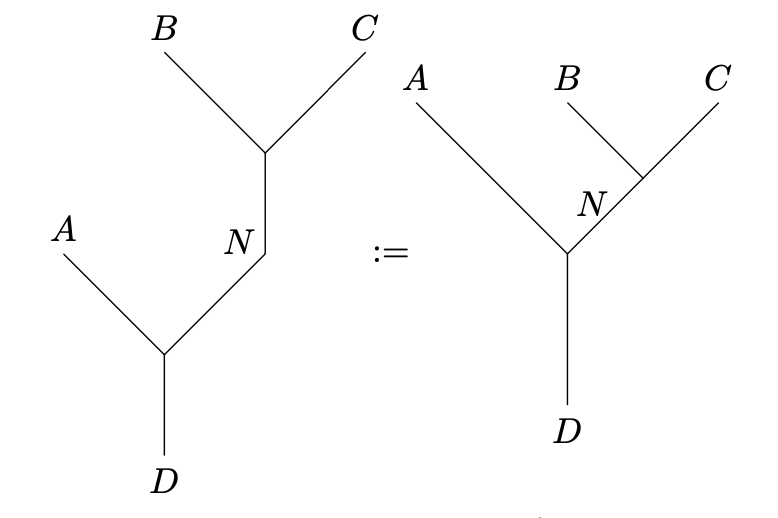
where in both cases ranges over representatives of isomorphism classes of simple objects.
Definition
The associator induces a map
for all simple objects . Expressing the source and target of this map in the distinguished bases above, we can canonically identify with a matrix.
The 6j symbol is defined to be the th coefficient of this matrix, where are isomorphism classes of simple objects. That is, the symbols are the unique complex numbers making the identity
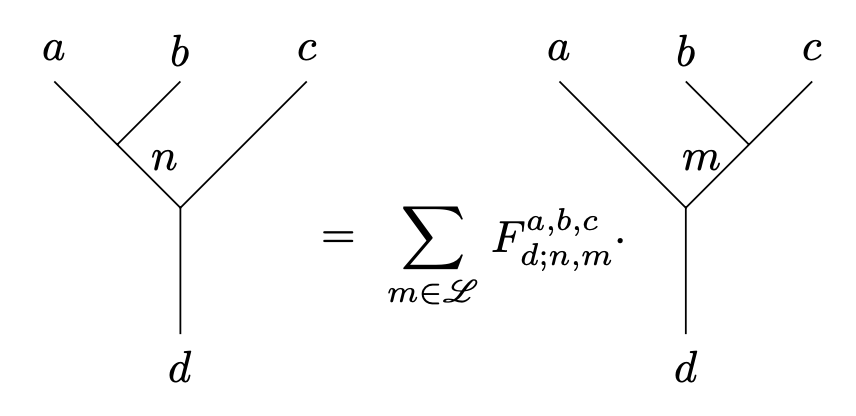
holds.
Use of Yoneda perspective
It is a key observation that one does not use the symbols to directly encode . Instead, the symbols are used to describe the action of the hom-space .
They key point is that objects are not associated vector spaces in a linear category: hom-spaces are. Hence, when encoding maps as matrices one has to take a dual perspective from objects to morphisms.
The Yoneda lemma exactly guarantees that the data encoded is enough to recover . Namely, knowing the action of on the hom-space for all simple objects one gets the full data of a natural transformation by the semisimplicity of . Because the Yoneda embedding is fully faithful, we can uniquely determine what map must have induces this natural transformation.
Related concepts
References
See also
- Gert Vercleyen. On Low-Rank Multiplicity-Free Fusion Categories (2024). (arXiv:2405.20075).
Last revised on May 31, 2024 at 09:01:21. See the history of this page for a list of all contributions to it.