nLab C2-equivariant homotopy groups of spheres
Content
Idea
-equivariant homotopy groups of spheres are particularly amenable to study because they are computed in a range by -motivic homotopy groups via real Betti realization with its Galois action;
this is special to among finite groups, since the Artin-Schreier theorem implies that it is the only nontrivial finite group occurring as an absolute Galois groups. (…)
-graded vs Mackey functor homotopy groups
In general, for all real orthogonal virtual -representations, we have a cofiber sequence of -spectra
In the case , we find that ; hence there is a natural long exact sequence in stable homotopy in the motivic grading , this reads as
In particular, the five lemma combined with the equivariant Whitehead theorem then proves the following (see Prop 3.2 of Guillou-Isaksen 24).
Proposition
A map of -spectra induces an isomorphism on -graded homotopy groups if and only if it induces an isomorphism on -graded mackey functor homotopy groups.
The corresponding theorem is seldom true for other groups, since every other group attains two dimensional irreducible real orthogonal -representations, whose compactifications will not be cofibers of -sets. For instance, a counterexample due to Clover May in the case appears as Ex. 3.1 of Guillou-Isaksen 24.
Relation to motivic homotopy groups
The following diagram appears on page 3 of Guillou-Isaksen 24.
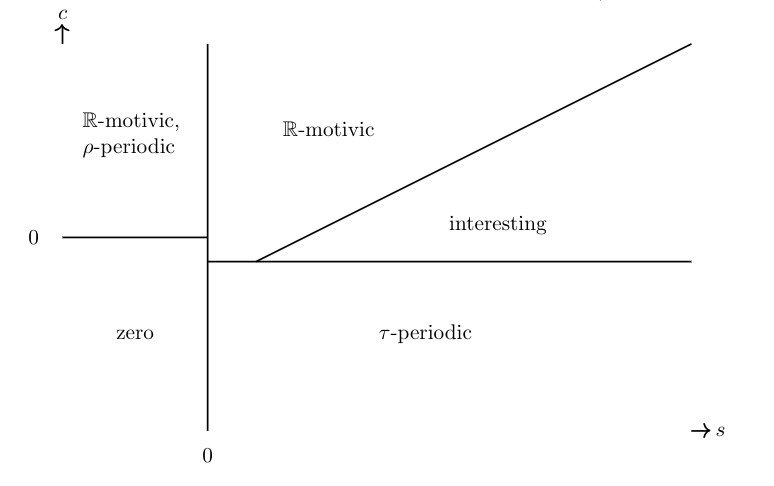
In this section, we will explain the regions. Explicitly:
The region
In Heller-Ormsby 14, given a finite Galois extension with Galois group , a symmetric monoidal functor
is constructed, which when evaluated on the endomorphism of the unit, yields the ring homomophism of Dress relating the Burnside ring to the Grothendieck-Witt ring?.
The following theorem is Theorem 1.1 of Heller-Ormsby 17 (with image shown in Heller-Ormsby 14).
Theorem
If is a real closed field and its algebraic closure, then the functor
is a fully faithful symmetric left adjoint whose image is generated under tensor products and colimits by finite etale -algebras.
This yields the corollary that is an isomorphism in degrees satisfying and . (Thm 3.11 Heller-Ormsby).
By relating the -motivic and -equivariant Adams -pages, Belmont-Guillou-Isaksen 21 improved this to the following to the following.
Theorem
The map is
-
an injection if , and
-
an isomorphism if and .
The region
Due to Bredon 67, as recalled e.g. in section 3.3 of Guillou-Isaksen 24, when and , there are periodicity isomorphisms which recognize negative coweight -equivariant homotopy groups as -power torsion subgroups of positive-coweight groups. (…)
The region
The spectral Mackey functor theorem quickly shows that any map is nullhomotopic when .
The region for small
(…)
Related concepts
References
-
Glen Bredon, Equivariant Stable Stems, (1967) (pdf)
-
Jeremiah Heller?, Kyle Ormsby?, Galois equivariance and stable motivic homotopy theory, (2014) (arXiv:1401.4728)
-
Jeremiah Heller?, Kyle Ormsby?, The stable Galois correspondence for real closed fields, (2016) (arXiv:1701.09099)
-
Eva Belmont?, Bertrand Guillou, Daniel Isaksen, -equivariant and -motivic stable stems, II, (2020) (arXiv:2001.02251v1)
-
Bertrand Guillou, Daniel Isaksen, -Equivariant Stable Stems, (2024) (arXiv:2404.14627)
Last revised on April 30, 2024 at 19:09:31. See the history of this page for a list of all contributions to it.