nLab braid category

Definition

The braid category $\mathbf{B}$ is the strict monoidal groupoid obtained as the disjoint union of all the braid groups $B_n$, $n \geq 0$ (thus, the coproduct of delooping groupoids in the category Grpd of groupoids).

The objects of $\mathbf{B}$ are thus identified with natural numbers $n$, and all morphisms are automorphisms $n \to n$ given by elements in braid groups $B_n$.

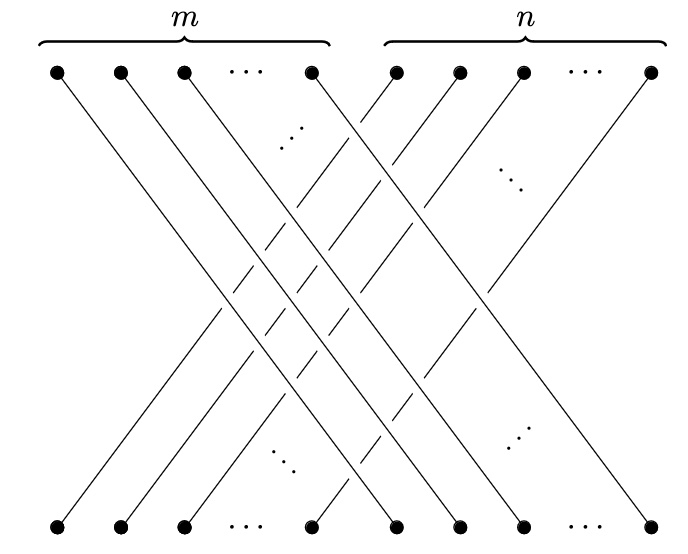
The monoidal product

$$\mathbf{B} \times \mathbf{B} \to \mathbf{B}$$

is given objectwise by addition of integers $n$, and on morphisms it is given by group homomorphisms

$$B_m \times B_n \to B_{m+n}$$

which may be described as juxtaposition of braids.

$\mathbf{B}$ is also a braided monoidal category, with the braiding $m+n \to n+m$ given by the “$m$-over-$n$” braid:

Properties

The braid category came into prominence with the celebrated paper Braided Monoidal Categories by Joyal and Street, who showed that the category of Artin braids (hitherto a thoroughly geometric construction) was the free braided (strict) monoidal category on the terminal category, and that the free braided monoidal category on a general category $C$ could be pictured as the category of braids whose strands are colored by morphisms in $C$.

Joyal and Street also showed that the braid category could be regarded as a “walking Yang-Baxter object”. Recall that a Yang-Baxter object? in a monoidal category $(M, \otimes, I)$ is an object $C$ equipped with an invertible “twist” map

$$R: C \otimes C \to C \otimes C$$

such that

$$\array{ C \otimes C \otimes C & \overset{R \otimes 1}{\to} & C \otimes C \otimes C & \overset{1 \otimes R}{\to} & C \otimes C \otimes C \\ 1 \otimes R \downarrow & & & & \downarrow R \otimes 1 \\ C \otimes C \otimes C & \underset{R \otimes 1}{\to} & C \otimes C \otimes C & \underset{1 \otimes R}{\to} & C \otimes C \otimes C }$$

commutes (as usually done, we work in strict monoidal categories for convenience). The statement now is that the braid category is initial in the category of strict monoidal categories equipped with a Yang-Baxter object. The $R$ in this case is a generator of $B_2 \cong \mathbb{Z}$, which is a braid with one crossing, and the commutativity may be pictured as an equality across a Reidemeister III move (and may be proven using the axioms of a braided monoidal category).

This result gave a conceptual framework in which to interpret quantum group representations as giving knot invariants.

Related concepts

• braid group

• vine monoid

• FinSet

• permutation category