nLab braid group
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Idea
By a braid group [Artin (1925)] one means the group of joint continuous motions [cf. Goldsmith (1981)] of a fixed number of non-coincident points in the plane, from any fixed configuration back to that fixed configuration. The “worldlines” traced out by such points in space-time under such an operation look like a braid with strands, whence the name.
As with actual braids, here it is understood that two such operations are identified if they differ only by continuous deformations of the “strands” without breaking or intersecting these, hence that one identifies those such systems of worldlines which are isotopic in . (This is just the kind of invariance considered for link diagrams — such as under Reidemeister moves — and in fact every link diagram may be obtained by “closing up” a braid diagram, in the evident sense.)
A quick way of saying this with precision is to observe that a braid group is thus the fundamental group of a configuration space of points in the plane (see below for more).
Here it makes a key difference whether:
-
one considers the points in a configuration as ordered (labeled by numbers ) in which case one speaks of the pure braid group,
-
or as indistinguishable (albeit in any case with distinct positions!) in which case one speaks of the braid group proper.
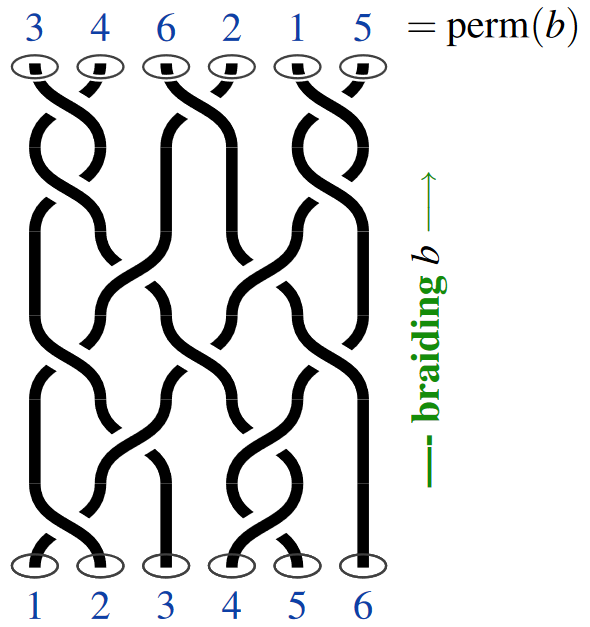
Namely, after traveling along a general braid the order of the given points may come out permuted by a permutation , and the braid is called pure precisely if this permutation is trivial:

More explicitly, braid groups admit finite presentations by generators and relations. To these we now turn first:
Definitions and characterizations
Via generators and relations
Presentation of general braids
We discuss the braid group as a finitely generated group (Artin 1925, (5)-(6); Artin 1947, (18)-(19); review in, e.g.: Fox & Neuwirth 1962, §7):
Definition
(Artin presentation)
The Artin braid group, , on strands is the finitely generated group given via generators and relations by (this and the following graphics are taken from Myers et al. (2023)):
-
generators:
(1)
-
relations I:
(2)
-
relations II (Yang-Baxter equation)
Presentation of pure braids
Similarly, the pure braid group has a finite presentation.
One possible set of generators (also originally considered by Artin) are the “weave” braids where one strands lassos exactly one other strand:
In terms of these generators, the pure braid group is obained by quotienting out the following relations — an optimization of Artin’s original pure braid relations, due to Lee (2010, Thm. 1.1, Rem. 3.1):
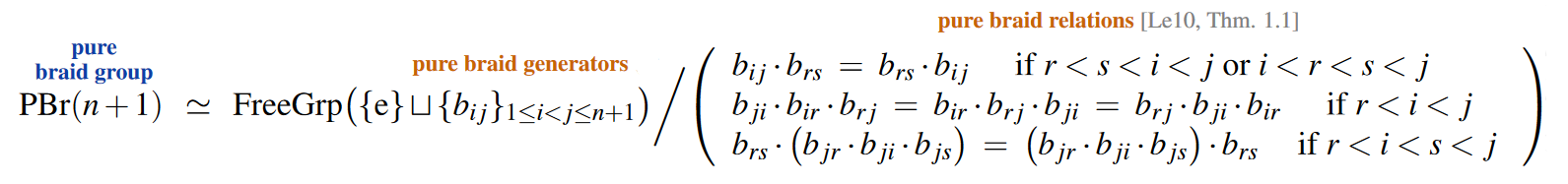
Here we repeatedly used products of pure braid generators of the following form:
As fundamental group of a configuration space of points
Geometrically, one may understand the group of braids in as the fundamental group of the configuration space of points in the plane (traditionally regarded as the complex plane in this context, though the complex structure plays no role in the definition of the braid group as such).
(originally due to Hurwitz 1891, §II, then re-discovered/re-vived in Fadell & Neuwirth 1962, p. 118, Fox & Neuwirth 1962, §7, review includes Birman 1975, §1, Williams 2020, pp. 9)
In the plane
We say this in more detail:
Let denote the space of configurations of n ordered points in the complex plane, whose elements are those n-tuples such that whenever . In other words, is the complement of the fat diagonal:
The symmetric group acts on by permuting coordinates. Let:
-
denote the quotient by this group action, hence the orbit space (the space of -element subsets of if one likes),
-
denote the image of under the quotient coprojection (i.e. its the equivalence class).
We understand as the basepoint for , and as the basepoint for the configuration space of unordered points , making it a pointed topological space.
Definition
The braid group is the fundamental group of the configuration space of n unordered points:
The pure braid group is the fundamental group of the configuration space of n ordered points:
Evidently a braid is represented by a path with . Such a path may be uniquely lifted through the covering projection to a path such that . The end of the path has the same underlying subset as but with coordinates permuted: . Thus the braid is exhibited by non-intersecting strands, each one connecting an to , and we have a map appearing as the quotient map of an exact sequence
which is part of a long exact homotopy sequence corresponding to the fibration .
In general surfaces or graphs
Since the notion of a configuration space of points makes sense for points in any topological space, not necessarily the plane , the above geometric definition has an immediate generalization:
For any surface, the fundamental group of the (ordered) configuration space of points in may be regarded as generalized (pure) braid group, called a surface braid group. (See the spherical braid group for the case that the surface in question is the 2-sphere.)
These surface braid groups are of interest in 3d topological field theory and in particular in topological quantum computation where it models non-abelian anyons.
Yet more generally, one may consider the fundamental group of the configuration space of points of any topological space .
For example for a 1-dimensional CW-complex, hence an (undirected) graph, one speaks of graph braid groups (e.g. Farley & Sabalka 2009).
The following should maybe not be here in the Definition-section, but in some Properties- or Examples-section, or maybe in a dedicated entry on graph braid groups?:
It has been shown (An & Maciazek 2006, using discrete Morse theory and combinatorial analysis of small graphs) that graph braid groups are generated by particular particle moves with the following description:
-
Star-type generators: exchanges of particle pairs on vertices of the particular graph
-
loop type generators: circular moves of a single particle around a simple cycle of the graph
Braid groups as mapping class groups of punctured surfaces
The braid groups are equivalently given by mapping class groups of punctured surfaces. [Birman 1969]
For plain braid groups
The braid group may be alternatively described as the mapping class group of a 2-disk with punctures. [Birman 1969]
(review includes Birman 1975 §4, González-Meneses 2011 §1.4, Massuyeau 2021 §3.3, Abadie 2022 §1.3)
Concretely, consider
-
denoting the complement of distinct points in the closed disk (with boundary the circle);
-
denoting the mapping space of auto-homeomorphisms which restrict to the identity on the boundary circle, regarded with its canonical group structure under composition;
-
denoting the subgroup which is the connected component of the identity (which is readily seen to be a normal subgroup).
Then the mapping class group is the quotient group:
Now observe that
-
for the case that this group is trivial, by Alexander's trick.
-
continuous extension yields an injection
Combining this implies that for every there is an isotopy to the identity, , under which the locations of the punctures trace out a braid (in the sense of a loop in the symmetrized configuration space of points). This construction constitutes a group homomorphism from the mapping class group to the braid group
and this is an isomorphism.
Remark
(action of braid group on fundamental group of -punctured disk)
It follows in particular that the braid group has a canonical group action on the fundamental group of the -punctured disk. Since the latter is isomorphic to the free group on generators, this leads to the purely algebraic characterization of the braid group below.
See also eg. Margalit & Winarski (2021), §7, Amram, Lawrence & Vishne (2012), §7.
For surface braid groups
More generally, let be a (connected) closed, oriented surface, possibly with boundary and let a finite set of interior points.
Then:
Proposition
The mapping class groups ()
-
(of itself, presering orientation and the boundary pointwise)
-
(of with “indistinguishable” punctures)
-
(of with “distinguishable” punctures)
relate to the surface braid groups
-
(ordinary braid group)
-
(pure braid group)
-
(the symmetric group)
by forming the following commuting diagram of group homomorphisms where all rows and all columns are exact sequences:
Corollary
When , then the long exact sequences of Prop. become short exact sequences:
(In this form the statement appears in Farb & Margalit 2012, Thm. 9.1.)
In words: The mapping class group of a punctured surface is a group extension of the mapping class group of the plain surface by the surface braid group on the set of punctures.
For conditions under which see here at diffeomorphism group.
Remark
The assumption in Cor. is necessary: Notably the statement fails for all -punctured spheres with (where Cor. would predict their mapping class groups to be isomorphic to the spherical braid groups while they are not, see there.
As automorphisms of a free group
Since the fundamental group of is the free group of generators, the MCG-presentation of the braid group (above) induces a group homomorphism of the braid group into the automorphism group of a free group, which turns out to be faithful.
This presentation is due to Artin 1925, §6, review includes González-Meneses 2011, §1.6, see also pointer in Bardakov 2005, p. 2.
More in detail, since the homotopy type of this punctured disk is, evidently, that of the the wedge sum of circles, it follows that its fundamental group is is the free group on generators:
Now the functoriality of implies we have an induced homomorphism
If such an automorphism of is isotopic to the identity, then of course is trivial, which means that the above homomorphism factors through the quotient group known as the mapping class group:
Therefore, the above gives a homomorphism of the following form, which turns out to be a monomorphism:
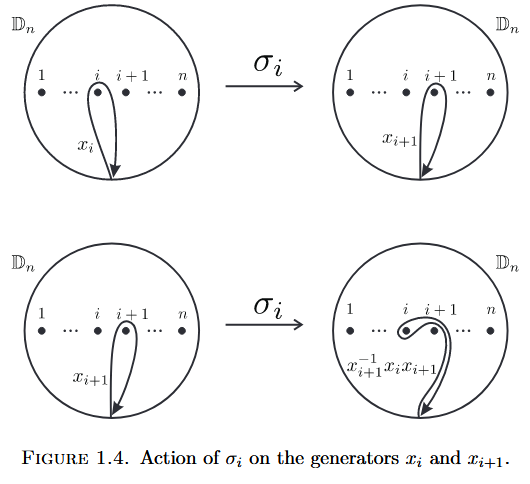
Explicitly, the generator (1) in the Artin presentation(Def. ) is mapped to the automorphism on the free group on generators which is given as follows:
Properties
Relation to moduli space of monopoles
Proposition
(moduli space of monopoles is stably weak homotopy equivalent to classifying space of braid group)
For there is a stable weak homotopy equivalence between the moduli space of k monopoles (?) and the classifying space of the braid group on strands:
Examples
The first few examples of the braid group for low values of :
Example
The group has no generators and no relations, so is the trivial group:
Example
The group has one generator and no relations, so is the infinite cyclic group of integers:
Example
The group (we will simplify notation writing , ) has presentation
This is also known as the “trefoil knot group”, i.e., the fundamental group of the complement of a trefoil knot.
Example
The Hurwitz braid group (or sphere braid group) is the surface braid group for the 2-sphere . Algebraically, the Hurwitz braid group has all of the generators and relations of the Artin braid group , plus one additional relation:
Related concepts
| chord diagrams | weight systems |
|---|---|
| linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams | Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems |
References
General
The braid group regarded as the fundamental group of a configuration space of points is considered (neither of them under these names, though) already in:
- Adolf Hurwitz, §II of: Über Riemann’sche Flächen mit gegebenen Verzweigungspunkten, Mathematische Annalen 39 (1891) 1–60 [doi:10.1007/BF01199469]
there regarded as acting on Riemann surfaces forming branched covers, by movement of the branch points.
The original articles dedicated to analysis of the braid group:
-
Emil Artin, Theorie der Zöpfe, Abh. Math. Semin. Univ. Hambg. 4 (1925) 47–72 [doi;10.1007/BF02950718]
(the braid group via generators & relations and via automorphisms of free groups)
-
Wilhelm Magnus, Über Automorphismen von Fundamentalgruppen berandeter Flächen, Mathematische Annalen 109 (1934) 617–646 [doi:10.1007/BF01449158]
(the braid group as a mapping class group)
-
Emil Artin, Theory of Braids, Annals of Mathematics, Second Series, 48 1 (1947) 101-126 [doi:10.2307/1969218]
-
Frederic Bohnenblust, The Algebraical Braid Group, Annals of Mathematics Second Series 48 1 (1947) 127-136 [doi:10.2307/1969219]
-
Wei-Liang Chow, On the Algebraical Braid Group, Annals of Mathematics Second Series, 49 3 (1948) 654-658 [doi:10.2307/1969050]
Identifying the center of the braid group as the subgroup generated by the square of the “fundamental braid” or “half-twist”:
- F. A. Garside: The braid group and other groups, The Quarterly Journal of Mathematics 20 1 (1969) 235–254 [doi:10.1093/qmath/20.1.235, pdf, pdf]
Survey of the early history:
- Michael Friedman (historian), Mathematical formalization and diagrammatic reasoning: the case study of the braid group between 1925 and 1950, British Journal for the History of Mathematics 34 1 (2019) 43-59 [doi:10.1080/17498430.2018.1533298]
The understanding of the braid group as the fundamental group of a configuration space of points was re-discovered/re-vived (after Hurwitz 1891) in:
-
Ralph H. Fox, Lee Neuwirth, The braid groups, Math. Scand. 10 (1962) 119-126 doi:10.7146/math.scand.a-10518, pdf, MR150755
-
Edward Fadell, Lee Neuwirth, Configuration spaces, Math. Scand. 10 (1962) 111-118 doi:10.7146/math.scand.a-10517, MR141126
The understanding of the braid group as the mapping class group of the punctured disk, etc., is due to:
- Joan S. Birman: Mapping class groups and their relationship to braid groups, Communications on Pure and Applied Mathematics 22 2 (1969) 213-238 [doi:10.1002/cpa.3160220206]
Textbook accounts:
-
Joan S. Birman, Braids, links, and mapping class groups, Princeton Univ Press (1975) [ISBN:9780691081496, preview pdf]
-
Saunders MacLane, §XI.4 of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (second ed. 1997) [doi:10.1007/978-1-4757-4721-8]
-
Tomotada Ohtsuki ch 2 of: Quantum Invariants – A Study of Knots, 3-Manifolds, and Their Sets, World Scientific (2001) [doi:10.1142/4746]
-
Seiichi Kamada: Classical Braids and Links, Part 1 of: Braid and Knot Theory in Dimension Four, Mathematical Surveys and Monographs 95, AMS (2002) [ISBN:978-0-8218-2969-1]
-
Christian Kassel, Vladimir Turaev, Braid Groups, GTM 247 Springer Heidelberg 2008 (doi:10.1007/978-0-387-68548-9, webpage)
In relation to mapping class groups:
- Benson Farb, Dan Margalit: Braid groups, chapter 9 of: A primer on mapping class groups, Princeton Mathematical Series, Princeton University Press (2012) [ISBN:9780691147949, jstor:j.ctt7rkjw, pdf]
Further introduction and review:
-
Joan S. Birman, Anatoly Libgober (eds.) Braids, Contemporary Mathematics 78 (1988) [doi:10.1090/conm/078]
-
Chen Ning Yang, M. L. Ge (eds.), Braid Group, Knot Theory and Statistical Mechanics, Advanced Series in Mathematical Physics 9, World Scientific (1991) [doi:10.1142/0796]
-
Dale Rolfsen: Tutorial on the braid groups, lecture notes (2007) [arXiv:1010.4051]
-
Joshua Lieber, Introduction to Braid Groups, 2011 (pdf)
-
Juan González-Meneses, Basic results on braid groups, Annales Mathématiques Blaise Pascal, 18 1 (2011) 15-59 [ambp:AMBP_2011__18_1_15_0, numdam:AMBP_2011__18_1_15_0]
-
Alexander I. Suciu, He Wang, The pure braid groups and their relatives, Perspectives in Lie theory, INdAM series, 19 Springer (2017) 403-426 [arXiv:1602.05291]
-
Dale Rolfsen: New developments in the theory of Artin’s braid groups, Topology and its Applications 127 1–2 (2003) 77-90 [doi:10.1016/S0166-8641(02)00054-8, pdf]
-
John Guaschi, Daniel Juan-Pineda: A survey of surface braid groups and the lower algebraic K-theory of their group rings [arXiv:1302.6536]
-
Jennifer C. H. Wilson, The geometry and topology of braid groups, lecture at 2018 Summer School on Geometry and Topology, Chicago (2018) [pdf, pdf]
-
Lucas Williams, Configuration Spaces for the Working Undergraduate, Rose-Hulman Undergraduate Mathematics Journal, 21 1 (2020) Article 8 [arXiv:1911.11186, rhumj:vol21/iss1/8]
-
Gwénaël Massuyeau: Lectures on Mapping Class Groups, Braid Groups and Formality (2021) [pdf, pdf]
-
Jennifer C. H. Wilson, Representation stability and the braid groups, talk at ICERM – Braids (Feb 2022) [pdf]
-
Marie Abadie, §1 in: A journey around mapping class groups and their presentations (2022) [pdf, pdf]
See also:
- Wikipedia: Braid group
As an example of motion general “motion groups” (such as loop braid groups):
- Deborah L. Goldsmith, The theory of motion groups, Michigan Math. J. 28 1 (1981) 3-17 [doi:10.1307/mmj/1029002454]
On presentations of surface braid groups:
- Paolo Bellingeri: On presentation of Surface Braid Groups [arXiv:math/0110129]
Algebraic presentation of braid groups:
-
Warren Dicks, Edward Formanek, around Ex. 15.2 of: Algebraic Mapping-Class Groups of Orientable Surfaces with Boundaries, in: Infinite Groups: Geometric, Combinatorial and Dynamical Aspects, Progress in Mathematics 248 Birkhäuser (2005) [doi :10.1007/3-7643-7447-0_4]
See also:
- E. A. Gorin, V. Ya. Lin: Algebraic equations with continuous coefficients and some problems of the algebraic theory of braids, Mathematics of the USSR-Sbornik 7 4 (1969) 569–596 [doi:10.1070/SM1969v007n04ABEH001104, mathnet:sm3572, pdf]
More finite presentations of the pure braid group:
-
Dan Margalit, Jon McCammond, Geometric presentations for the pure braid group, Journal of Knot Theory and Its Ramifications 18 01 (2009) 1-20 [arXiv:math/0603204, doi:10.1142/S0218216509006859]
-
Eon-Kyung Lee, A positive presentation of the pure braid group, Journal of the Chungcheong Mathematical Society 23 3 (2010) 555-561 [JAKO201007648745187, pdf]
On the framed braid group:
-
Ki Hyoung Ko, Lawrence Smolinsky: The framed braid group and 3-manifolds, Proc. Amer. Math. Soc. 115 (1992) 541-551 [doi:10.1090/S0002-9939-1992-1126197-1, pdf]
-
Ki Hyoung Ko, Lawrence Smolinsky: The framed braid group and representations, in: Knots 90, Proceedings in Mathematics, De Gruyter (1992) 289-297 [doi:10.1515/9783110875911, pdf]
-
R. Krasauskas: Crossed simplicial groups of framed braids and mapping class groups of surfaces, Lith Math J 36 (1996) 263–281 [doi:10.1007/BF02986853]
-
Akishi Ikeda: Homological and Monodromy Representations of Framed Braid Groups, Commun. Math. Phys. 359 (2018) 1091–1121 [doi:10.1007/s00220-017-3036-1, arXiv:1702.03918]
-
Marco De Renzi, Azat M. Gainutdinov, Nathan Geer, Bertrand Patureau-Mirand, Ingo Runkel, §3.1 in: Mapping Class Group Representations From Non-Semisimple TQFTs, Commun. Contemp. Math. (2021) 2150091 [arXiv:2010.14852, doi:10.1142/S0219199721500917]
(in the context of Reshetikhin-Turaev TQFT)
-
Ying Hong Tham: §3.2.1 in: On the Category of Boundary Values in the Extended Crane-Yetter TQFT, PhD thesis, Stony Brook (2021) [arXiv:2108.13467]
(in the context of the Crane-Yetter model)
-
Iordanis Romaidis, pp 37 in: Mapping class group actions and their applications to 3D gravity, PhD thesis, Hamburg (2022) [ediss:9945]
(in the context of Reshetikhin-Turaev TQFT)
-
Iordanis Romaidis, Ingo Runkel, p. 8 of: CFT correlators and mapping class group averages [arXiv:2309.14000]
(in the context of Reshetikhin-Turaev TQFT)
-
Lukas Woike: The Cyclic and Modular Microcosm Principle in Quantum Topology [arXiv:2408.02644]
(in relation to the framed little disk operad)
-
Anastasios Kokkinakis: Framed Braid Equivalences [arXiv:2503.05342]
More on the relation of braid groups to mapping class groups:
-
M. Amram, R. Lawrence, U. Vishne, Artin Covers of the Braid Group, Journal of Knot Theory and Its Ramifications 21 07 (2012) 1250061 [doi:10.1142/S0218216512500617, pdf]
-
Dan Margalit, Rebecca R. Winarski, Braid groups and mapping class groups: The Birman–Hilden theory, Bull. London Math. Soc. 53 3 (2021) 643-659 [arXiv:1703.03448, doi:10.1112/blms.12456]
-
Paolo Bellingeri, Sylvain Gervais: Surface framed braids, Geom Dedicata 159 (2012) 51–69 [doi:10.1007/s10711-011-9645-5, arXiv:1001.4471]
More on the braid representation on automorphisms of free groups:
-
Lluís Bacardit, Warren Dicks, Actions of the braid group, and new algebraic proofs of results of Dehornoy and Larue, Groups Complexity Cryptology 1 (2009) 77-129 [arXiv:0705.0587, doi;10.1515/GCC.2009.77]
-
Valerij G. Bardakov, Extending representations of braid groups to the automorphism groups of free groups, Journal of Knot Theory and Its Ramifications 14 08 (2005) 1087-1098 [arXiv:math/0408330, doi:10.1142/S0218216505004251]
-
Tetsuya Ito, Actions of the -strand braid groups on the free group of rank n which are similar to the Artin representation, Quart. J. Math 66 (2015) 563-581 [arXiv;1406.2411, doi:10.1093/qmath/hau033]
On the group homology and group cohomology of braid groups:
- Vladimir Vershinin, Homology of Braid Groups and their Generalizations, Banach Center Publications (1998) 42 1 421-446 (pdf, dml:208821)
Relation of automorphism groups of the profinite completion of braid groups to the Grothendieck-Teichmüller group:
- Pierre Lochak, Leila Schneps, The Grothendieck-Teichmüller group and automorphisms of braid groups, in: The Grothendieck Theory of Dessins d’Enfant, Cambridge University Press (1994, 2011) [pdf, doi:10.1017/CBO9780511569302]
On braid subgroups:
-
Dale Rolfsen: Braid subgroup normalisers, commensurators and induced representations, Invent Math 130 (1997) 575–587 [doi:10.1007/s002220050194, pdf]
-
D. B. McReynolds: The congruence subgroup problem for braid groups: Thurston’s proof, New York Jour. Math. 18 (2012) 925-942 [arXiv:0901.4663]
-
Charalampos Stylianakis: Congruence subgroups of braid groups, International Journal of Algebra and Computation 28 02 (2018) 345-364 [doi:10.1142/S0218196718500169]
On orderings of the braid group:
-
Patrick Dehornoy: Braid groups and left distributive operations, Transactions AMS 345 1 (1994) 115150 [doi:10.1090/S0002-9947-1994-1214782-4, pdf]
-
H. Langmaack, Verbandstheoretische Einbettung von Klassen unwesentlich verschiedener Ableitungen in die Zopfgruppe , Computing 7 no.3-4 (1971) pp.293-310.
On geometric presentations of braid groups:
- Byung Hee An, Tomasz Maciazek, Geometric Presentations of Braid Groups for Particles on a Graph, Communications in Mathematical Physics 384 (2021) 1109-1140 [doi:10.1007/s00220-021-04095-x]
On G-structure for the infinite braid group:
-
Frederick R. Cohen, Braid orientations and bundles with flat connections, Inventiones mathematicae 46 (1978) 99–110 [doi:10.1007/BF01393249]
-
Jonathan Beardsley, On Braids and Cobordism Theories, Glasgow (2022) [notes: pdf, pdf]
Braid group representations (as topological quantum gates)
On linear representations of braid groups (see also at braid group statistics and interpretation as quantum gates in topological quantum computation):
- Ivan Marin, On the representation theory of braid groups, Annales mathématiques Blaise Pascal, 20 2 (2013) 193-260 (arXiv:math/0502118, dml:275607)
Review:
-
Chen Ning Yang, M. L. Ge (eds.). Braid Group, Knot Theory and Statistical Mechanics, Advanced Series in Mathematical Physics 9, World Scientific (1991) doi:10.1142/0796
(focus on quantum Yang-Baxter equation)
-
Camilo Arias Abad: Introduction to representations of braid groups, Rev. colomb. mat. 49 1 (2015) [doi:10.15446/recolma.v49n1.54160, arXiv:1404.0724]
-
Toshitake Kohno, Introduction to representation theory of braid groups, Peking 2018 (pdf, pdf)
in relation to modular tensor categories:
- Colleen Delaney, Lecture notes on modular tensor categories and braid group representations, 2019 (pdf, pdf)
Braid representations from the monodromy of the Knizhnik-Zamolodchikov connection on bundles of conformal blocks over configuration spaces of points:
-
Ivan Todorov, Ludmil Hadjiivanov, Monodromy Representations of the Braid Group, Phys. Atom. Nucl. 64 (2001) 2059-2068; Yad.Fiz. 64 (2001) 2149-2158 arXiv:hep-th/0012099, doi:10.1134/1.1432899
-
Ivan Marin, Sur les représentations de Krammer génériques, Annales de l’Institut Fourier, 57 6 (2007) 1883-1925 numdam:AIF_2007__57_6_1883_0
and understood in terms of anyon statistics:
- Xia Gu, Babak Haghighat, Yihua Liu, Ising- and Fibonacci-Anyons from KZ-equations, J. High Energ. Phys. 2022 15 (2022) [doi:10.1007/JHEP09(2022)015, arXiv:2112.07195]
Braid representations seen inside the topological K-theory of the braid group‘s classifying space:
-
Alejandro Adem, Daniel C. Cohen, Frederick R. Cohen, On representations and K-theory of the braid groups, Math. Ann. 326 (2003) 515-542 (arXiv:math/0110138, doi:10.1007/s00208-003-0435-8)
-
Frederick R. Cohen, Section 3 of: On braid groups, homotopy groups, and modular forms, in: J.M. Bryden (ed.), Advances in Topological Quantum Field Theory, Kluwer 2004, 275–288 (pdf)
See also:
- R. B. Zhang, Braid group representations arising from quantum supergroups with arbitrary and link polynomials, Journal of Mathematical Physics 33, 3918 (1992) (doi:10.1063/1.529840)
As quantum gates for topological quantum computation with anyons:
-
Louis H. Kauffman, Samuel J. Lomonaco, Braiding Operators are Universal Quantum Gates, New Journal of Physics 6 (2004) [doi:10.1088/1367-2630/6/1/134, arXiv:quant-ph/0401090]
(via R-matrix solutions to the quantum Yang-Baxter equation)
-
Yong Zhang, Louis H. Kauffman, Mo-Lin Ge: Yang–Baxterizations, Universal Quantum Gates and Hamiltonians, Quantum Inf Process 4 (2005) 159–197 [doi:10.1007/s11128-005-7655-7]
(via R-matrix solutions to the quantum Yang-Baxter equation)
-
Samuel J. Lomonaco, Louis Kauffman, Topological Quantum Computing and the Jones Polynomial, Proc. SPIE 6244, Quantum Information and Computation IV, 62440Z (2006) (arXiv:quant-ph/0605004)
(braid group representation serving as a topological quantum gate to compute the Jones polynomial)
-
Louis H. Kauffman, Samuel J. Lomonaco, Topological quantum computing and braid group representations, Proceedings Volume 6976, Quantum Information and Computation VI; 69760M (2008) (doi:10.1117/12.778068, rg:228451452)
-
C.-L. Ho, A. I. Solomon, C.-H. Oh: Quantum entanglement, unitary braid representation and Temperley-Lieb algebra, EPL 92 (2010) 30002 [doi:10.1209/0295-5075/92/30002, arXiv:1011.6229]
-
Rebecca Chen: Generalized Yang-Baxter Equations and Braiding Quantum Gates, Journal of Knot Theory and Its Ramifications 21 09 (2012) 1250087 [arXiv:1108.5215, doi:10.1142/S0218216512500873]
-
Louis H. Kauffman, Majorana Fermions and Representations of the Braid Group, International Journal of Modern Physics A 33 23 (2018) 1830023 [doi:10.1142/S0217751X18300235, arXiv:1710.04650]
-
David Lovitz, Universal Braiding Quantum Gates [arXiv:2304.00710]
Introduction and review:
-
Colleen Delaney, Eric C. Rowell, Zhenghan Wang, Local unitary representations of the braid group and their applications to quantum computing, Revista Colombiana de Matemáticas(2017), 50 (2):211 (arXiv:1604.06429, doi:10.15446/recolma.v50n2.62211)
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing arXiv:2208.11762
Realization of Fibonacci anyons on quasicrystal-states:
- Marcelo Amaral, David Chester, Fang Fang, Klee Irwin, Exploiting Anyonic Behavior of Quasicrystals for Topological Quantum Computing, Symmetry 14 9 (2022) 1780 arXiv:2207.08928, doi:10.3390/sym14091780
Realization on supersymmetric spin chains:
- Indrajit Jana, Filippo Montorsi, Pramod Padmanabhan, Diego Trancanelli, Topological Quantum Computation on Supersymmetric Spin Chains arXiv:2209.03822
Graph braid groups
-
Daniel Farley, Lucas Sabalka, Presentations of Graph Braid Groups (arXiv:0907.2730)
-
Ki Hyoung Ko, Hyo Won Park, Characteristics of graph braid groups (arXiv:1101.2648)
-
Byung Hee An, Tomasz Maciazek, Geometric presentations of braid groups for particles on a graph (arXiv:2006.15256)
Relation to moduli space of monopoles
On moduli spaces of monopoles related to braid groups:
-
Fred Cohen, Ralph Cohen, B. M. Mann, R. J. Milgram, The topology of rational functions and divisors of surfaces, Acta Math (1991) 166: 163 (doi:10.1007/BF02398886)
-
Ralph Cohen, John D. S. Jones Monopoles, braid groups, and the Dirac operator, Comm. Math. Phys. Volume 158, Number 2 (1993), 241-266 (euclid:cmp/1104254240)
Braid group cryptography
Partly motivated by the possibility of quantum computation eventually breaking the security of cryptography based on abelian groups, such as elliptic curves, there are proposals to use non-abelian braid groups for purposes of cryptography (“post-quantum cryptography”).
Via Conjugacy Search
An early proposal was to use the Conjugacy Search Problem in braid groups as a computationally hard problem for cryptography. This approach, though, was eventually found not to be viable.
Original articles:
-
Iris Anshel, M. Anshel and D. Goldfeld, An algebraic method for public-keycryptography, Math. Research Letters 6 (1999), 287–291 (pdf)
-
K.H. Ko, S.J. Lee, J.H. Cheon , J.W. Han, J. Kang, C. Park , New Public-Key Cryptosystem Using Braid Groups, In: M. Bellare (ed.) Advances in Cryptology — CRYPTO 2000 Lecture Notes in Computer Science, vol 1880. Springer 2000 (doi:10.1007/3-540-44598-6_10)
Review:
-
Karl Mahlburg, An Overview of Braid Group Encryption, 2004 (pdf)
-
Parvez Anandam, Introduction to Braid Group Cryptography, 2006 (pdf)
-
David Garber, Braid Group Cryptography, Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore (arXiv:0711.3941, doi:10.1142/9789814291415_0006)
-
Cryptowiki, Cryptosystems based on braid groups
Via E-multiplication
A followup proposal was to use the problem of reversing E-multiplication in braid groups, thought to remedy the previous problems.
Original article:
- Iris Anshel, Derek Atkins, Dorian Goldfeld and Paul E Gunnells, WalnutDSA(TM): A Quantum-Resistant Digital Signature Algorithm (eprint:2017/058)
Review:
- Magnus Ringerud, WalnutDSA: Another attempt at braidgroup cryptography, 2019 (pdf)
But other problems were found with this approach, rendering it non-viable.
Original article:
- Matvei Kotov, Anton Menshov, Alexander Ushakov, An attack on the Walnut digital signature algorithm, Designs, Codes and Cryptography volume 87, pages 2231–2250 (2019) (doi:10.1007/s10623-019-00615-y)
Review:
- José Ignacio Escribano Pablos, María Isabel González Vasco, Misael Enrique Marriaga and Ángel Luis Pérez del Pozo, The Cracking of WalnutDSA: A Survey, in: Interactions between Group Theory, Symmetry and Cryptology, Symmetry 2019, 11(9), 1072 (doi:10.3390/sym11091072)
Further developments
The basic idea is still felt to be promising:
-
Xiaoming Chen, Weiqing You, Meng Jiao, Kejun Zhang, Shuang Qing, Zhiqiang Wang, A New Cryptosystem Based on Positive Braids (arXiv:1910.04346)
-
Garry P. Dacillo, Ronnel R. Atole, Braided Ribbon Group -based Asymmetric Cryptography, Solid State Technology Vol. 63 No. 2s (2020) (JSST:5573)
But further attacks are being discussed:
- James Hughes, Allen Tannenbaum, Length-Based Attacks for Certain Group Based Encryption Rewriting Systems (arXiv:cs/0306032)
As are further ways around these:
- Xiaoming Chen, Weiqing You, Meng Jiao, Kejun Zhang, Shuang Qing, Zhiqiang Wang, A New Cryptosystem Based on Positive Braids (arXiv:1910.04346)
Last revised on May 5, 2025 at 07:39:59. See the history of this page for a list of all contributions to it.