nLab flat K-theory

Idea

In the context of topological K-theory (at least), flat K-theory (first considered in Karoubi 1987, §7.21, 1990, Ex. 3) is the Whitehead-generalized cohomology theory which is (represented by) the homotopy fiber of the Chern character; equivalently the restriction (namely the homotopy pullback) of differential K-theory (any version of it) to vanishing generalized-curvature.

Since the coefficients of flat KU form the circle group $U(1) \simeq \mathbb{R}/\mathbb{Z}$, flat K-theory is also known as $\mathbb{R}/\mathbb{Z}$-K-theory or as K-theory with $\mathbb{R}/\mathbb{Z}$-coefficients (Lott 1994), or similar.

In the differential cohomology hexagon for topological K-theory, flat K-theory appears in outer long exact sequence (Simons & Sullivan 2008, p. 2):

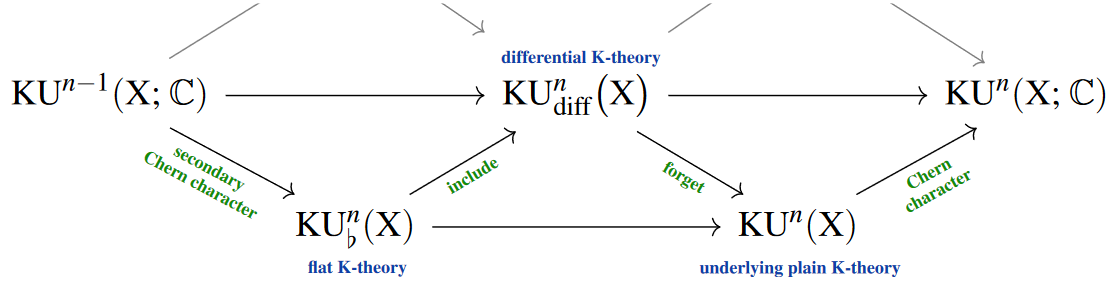
(graphics from SS22)

Related concepts

• differential K-theory

• flat connection

• flat vector bundle

• secondary characteristic class

• differential cohomology hexagon

References

Original accounts:

• Max Karoubi, §7.21 in: Homologie cyclique et K-théorie, Astérisque, 149 (1987) 156 $[$numdam:AST_1987__149__1_0$]$

• Max Karoubi, Ex. 3 in: Théorie générale des classes caractéristiques secondaires, K-Theory 4 1 (1990) 55-87 $[$doi:10.1007/BF00534193$]$

• John Lott, (16) in: $\mathbf{R}/\mathbf{Z}$ index theory, Communications in Analysis and Geometry 2 2 (1994) 279-311 $[$doi:10.4310/CAG.1994.v2.n2.a6$]$

Discussion as a vertex in the differential cohomology hexagon:

• James Simons, Dennis Sullivan, p. 2 of: Structured vector bundles define differential K-theory, Astérisque, 321 (2008) $[$arXiv:0810.4935, numdam:AST_2008__321__1_0$]$