nLab lax 2-adjunction
Contents
Idea
A lax 2-adjunction is an adjunction ‘up to adjointness’. A 1-categorical adjunction is given by a natural isomorphism of hom-sets
A strict 2-adjunction is analogous, where are instead strict 2-categories, are strict 2-functors, and is a strictly 2-natural isomorphism of hom-categories, while a biadjunction or pseudoadjunction allows all of these to be “weak up to isomorphism”.
A lax 2-adjunction is instead given by a (suitably natural) pair of families of functors
such that for each we have an adjunction . Independently of this laxness aspect, we can make a choice of weakness or strictness for the categories, functors, and natural transformations involved; thus one might speak of “lax biadjunctions”, “lax pseudoadjunctions”, and so on.
It is not entirely clear that the term “lax 2-adjunction” is appropriate; in particular it is not an instance of the general notion of lax algebras, unlike nearly all other usages of the word “lax”. Other terms that have been used for the same or similar notions are “transcendental quasi-adjunction” (Gray) and “local adjunction” (Betti-Power).
Definition
Just as the notion of adjunction makes sense not just in but in any 2-category, lax 2-adjunctions can be defined in any (possibly weak) 3-category when the above is suitably reformulated by using the 2-categorical Yoneda lemma. So, given 0-cells and 1-cells , in any 3-category, we say is lax left adjoint to if we have
-
2-cells and , and
-
instead of strict triangle equalities, 3-cells (called triangulators)
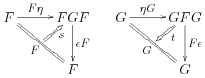
satisfying the swallowtail identities:
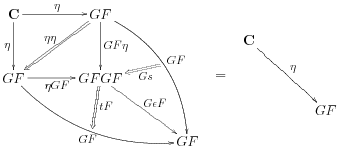
and
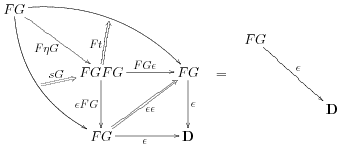
(where if the 3-category is weak then coherences might need to be inserted to make these make sense.
When interpreted in a strict 3-category , the Gray-category , or the tricategory , this yields three levels of weakness of “lax 2-adjunction” according to whether the categories, functors, and/or transformations are strict or pseudo.
Further generalizations
The following remarks are incomplete.
One can additionally generalize to allow and to be lax natural transformations. Gray’s original notion of “transcendental quasi-adjunction” did this, with the 2-categories and 2-functors being strict. Lax transformations do not live in any 3-category as usually understood, but Gray’s particular case can be done in the “lax Gray-category” .
Note also that there is no Yoneda lemma for lax transformations (though there is for pseudo ones). So in order for to be determined by , must be pseudo natural in , and likewise for to be determined by , it must be pseudo natural in . My guess is that laxity in the remaining variable will correspond to laxity of and , and will come from the adjunction . Another option is to require and to be pseudo natural on wide subcategories that include their components; see lax F-adjunction for an abstract context for such a definition.
One might additionally consider allowing the functors to be lax, as in (Betti-Power) (Seely). But lax functors are even harder to incorporate in a 3-category-like structure than lax transformations, since one can’t even whisker any sort of transformation by a lax functor. Seely also seems to say that and are both strict in their first coordinate, rather than one in the first and one in the second as seems (to me) to be necessary for a Yoneda restatement.
Related concepts
References
- Gray-adjointness-for-2-categories referred to a lax 2-adjunction as a transcendental quasi-adjunction.
- Renato Betti and John Power, On Local Adjointness of Distributive Bicategories
- Seely, Modelling computations: a 2-categorical framework, pdf
Last revised on October 30, 2023 at 07:27:16. See the history of this page for a list of all contributions to it.