nLab primitive element
(This article is about primitive elements in coalgebra theory, not about primitive elements for finite field extensions.)
Context
Algebra
Algebraic theories
Algebras and modules
Higher algebras
-
symmetric monoidal (∞,1)-category of spectra
Model category presentations
Geometry on formal duals of algebras
Theorems
Contents
Definition
Working over a commutative ring , recall that a unital or coaugmented coalgebra is an -coalgebra equipped with a coalgebra map . Abusing notation, denote by .
Primitive element in a coalgebra
An element in a coalgebra is primitive if . This condition implies .
This notion generalizes straightforwardly to unital corings over and even more generally to any unital comonoid object in a CMon-enriched monoidal category (see below).
Primitive element in a comodule
Let be a comodule over , with co-action map . Then an element is called a primitive element or coinvariant if .
The -module of primitive elements of is naturally to
-
the module of comodule homomorphisms out of into
-
the cotensor product of with
Object of primitive elements of a unital comonoid in a -enriched monoidal category
Let be a unital comonoid object in a CMon-enriched monoidal category . The object of primitive elements of is defined if it exists, as the equalizer in this diagram:
Proposition
If the unital comonoid admits an object of primitive elements, the commutative rig verifies , and the homsets [A,B] are multiplicatively cancellative modules over , we then have:
Proof
In this diagram, the path from to by the upper square (with below side equal to ) is equal to the identity and the two paths from to are equal:
We thus have that:
and:
We then have: 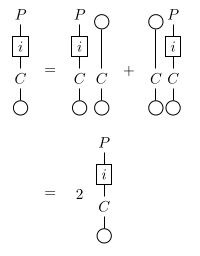
being a multiplicatively cancellative -module, if , we would have that in which is false, therefore .
Properties
Primitives in a Hopf algebra
A straightforward calculation shows that the module of primitive elements in a Hopf algebra (or even in a bialgebra ) is a Lie subalgebra of the underlying Lie algebra of (whose bracket is the algebra commutator). Thus, taking primitive elements yields a functor
(and of course we have more generally a functor which is an extension along the full inclusion ).
For a Lie algebra , let be its universal enveloping algebra:
where is the two-sided ideal generated by elements of the form where . This carries a bialgebra structure whose comultiplication is uniquely determined by the rule for . Since this says is primitive, the counit is forced to be the algebra map such for all , and also the Hopf antipode is uniquely determined: for .
The following proposition is entirely straightfoward:
Proposition
The functor is left adjoint to the functor .
This result is essentially tautologous and holds for any commutative ring of arbitrary characteristic. (This despite the fact that the as defined above is not as well-behaved in nonzero characteristic as one might like; e.g. the PBW theorem fails.) More information on this adjunction may require more restrictive hypotheses:
Proposition
For a field of characteristic zero, the unit is an isomorphism.
An immediate consequence is that for such ground fields , the functor is fully faithful. Of course, lands in the full subcategory of cocommutative Hopf algebras, which is exactly the category of group objects in the cartesian monoidal category of cocommutative coalgebras.
The Milnor-Moore theorem gives further information: for Hopf algebras over a field of characteristic zero, the counit is a monomorphism, and an isomorphism in case satisfies a suitable conilpotency condition.
(More needs to be added.)
Last revised on February 2, 2025 at 08:59:04. See the history of this page for a list of all contributions to it.