nLab monad

This entry is about the notion of monad in category theory and categorical algebra. For other notions see monad (disambiguation).

---

Idea

In category theory, the notion of monad (earlier: “standard construction” or “triple”) is a kind of categorification of that of monoid: In their default incarnation monads are endofunctors on some category which are equipped with a unital associative binary operation under composition. More generally this notion makes sense for endo- 1-morphisms on any object in any 2-category beyond Cat: Monads are monoid objects internal to endo-hom-categories.

Together with the adjunctions (adjoint functors) that they correspond to (see below) monads are among the most pervasive structures in category theory (where they form the basis of categorical and universal algebra, whence one speaks of algebras over a monad) and in mathematics more generally (certainly in fields like algebraic topology, sheaf and topos theory and homological algebra, where the notion originates in the guise of “canonical resolutions”).

Last not least, monads play a central role in formal logic (cf. modal logic and modal type theory) and in computer science, where they are understood (cf. the “computational trilogy”) as encoding “notions of computation” with “computational effects” in the framework of functional programming: see at monads in computer science.

Etymology

The terminology “monad” was introduced in Bénabou 1967, Def. 5.4.1, where, after observing (Exp. 5.4.1) that monads in 1-object 2-categories (deloopings of monoidal categories) are monoids:

it says in a footnote:

(from Bénabou 1967, p. 40)

Beyond this footnote, the only contemporary account that seems to exist of the terminological genesis, Barr 2009, recalls the following exchange, on the backdrop of a widely felt dissatisfaction with the earlier terminology of “standard construction” and “triple”:

In the summer (or maybe late spring, the Oberwohlfach records will show this) of 1966, there was a category meeting there. […] One day at lunch or dinner I happened to be sitting next to Jean Bénabou and he turned to me and said something like “How about `monad'?" I thought about and said it sounded pretty good to me. So Jean proposed it to the general audience and there was general agreement. It suggested "monoid" of course and it is a monoid in a functor category.

Further discussion on the issue in 2023 has recollections by Jirí Adámek of recollections by Bill Lawvere to the extent that:

it was in the common room of the old castle at Oberwolfach when Sammy [Samuel Eilenberg] came out from behind the piano and announced the change.

But Michael Barr clarifies that:

I am more than willing to believe that it was Bénabou sitting next to me who proposed monad. It is entirely possible that Sammy came down and pronounced it “official”. And it was certainly in the old castle.

Interestingly Bénabou’s footnote above gives a second motivation for “monad”:

(from Bénabou 1967, p. 39)

It is striking that Bénabou 1967, Def. 5.4.1 defines a monad to be a lax 2-functor from the terminal category $1$ to the 2-category of categories (and more generally to whatever given ambient 2-category “$\underline{S}$”) and then proceeds to unwind the equivalence of this definition to the traditional one:

$$Monads(\underline{S}) \;\;\; \simeq \;\;\; \Big\{ 1 \xrightarrow{\; lax \;} \underline{S} \Big\} \,.$$

In this sense, monads are point-like elements in a 2-category theoretic sense (say in the 2-topos Cat), which squares well with Euclid’s ancient notion of monads as indivisible building blocks. In fact, as discussed there, “monad” (both in ancient and still in modern Greek) just means “unit” in the sense of the unit natural number $1$, and Bénabou 1967, Def. 5.4.1 literally identifies monads with the (lax) units $1 \to \underline{S}$ in the ambient 2-category.

In generalization of this situation, one may consider lax functors out of codiscrete groupoids $CoDisc(1^{\sqcup_n})$ on $n$ objects, which Bénabou 1967, Def. 5.5 calls polyads:

$$Polyads(\underline{S}) \;\;\; \simeq \;\;\; \Big\{ CoDisc(1^{\sqcup_n}) \xrightarrow{\; lax \;} \underline{S} \Big\} \,.$$

On the other hand (as maybe alluded to in the first line of Barr 2009), just a few years earlier the ancient monad terminology had already been adopted in nonstandard analysis as the term for infinitesimal neighbourhoods (Robinson 1966, p. 57 and Luxembourg 1966, compare also Keisler 1976, Def. 1.2, Kutateladze 2011 and, speaking synthetically: Kock 1980).

Now it so happens — in the topos theoretic formulation of infinitesimals via differential cohesion — that the construction of infinitesimal neighbourhoods is (see here) a monad in the sense of category theory! – namely the left adjoint monad to the jet comonad (Khavkine & Schreiber 2017, p. 23).

Definition

Monads

A monad in a bicategory $K$ is given by

1. an object $a$ in $K$

2. an endomorphism $t \colon a \to a$ in $K$

3. a 2-morphism $\;\eta \colon 1_a \to t$ in $K$

   (the unit or return operation)

4. a 2-morphism $\mu \colon t \circ t \to t$

   (the multiplication or join operation)

such that the diagrams commute (where certain coherence isomorphisms have been omitted).

The name “monad” and the terms “unit”, “multiplication” and “associativity” bear a clear analogy with monoids (but see also at monad (disambiguation)). Indeed, one can define a monad on an object $a$ of a bicategory $K$ as just a monoid object in the endomorphism category $K(a,a)$. Alternatively, monads can be taken as more fundamental, and a monoid in a monoidal category $C$ can be defined as a monad in $\mathbf{B} C$, the one-object bicategory corresponding to $C$.

A third and somewhat less obvious definition says that a monad in $K$ is a lax 2-functor from the terminal bicategory $1$ to $K$: the unique object $\ast$ of $1$ is sent to the object $a$, the morphism $1_a$ becomes $t$, and $\eta$ and $\mu$ arise from the coherent 2-cells expressing lax functoriality. This in turn is equivalent to saying that a monad is a category enriched in a bicategory with a single object and single morphism. Among higher-category theorists, it’s tempting to suggest that this is the most fundamental definition, and the most basic reason for the ubiquity and importance of monads. Regardless of this, however, the earlier more elementary definitions are both practically and pedagogically essential.

Finally, a monad can be defined in terms of the “Kleisli operation” taking any map $a \to T b$ to a map $T a \to T b$; see extension system.

We can picture a monad in $K$ as an image of the third oriental in $K$. See the remarks at monoidal category.

The data of and axioms for a monad can be expressed graphically as string diagrams. Writing $T \colon C \to C, \eta, \mu$ for the monad in question (this notation being the standard one when $K = Cat$), these data can be represented as

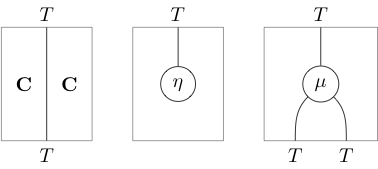
Thanks to the distinctive shapes, one can usually omit the labels:

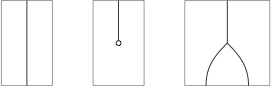
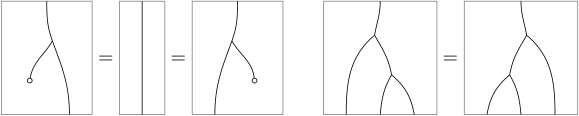
The axioms then appear as:

The 2-category of monads

Given the equivalence between monads in a 2-category $K$ and lax functors $1 \to K$ [Bénabou 1967, pp. 39] it is straightforward to define the 2-category $Mnd(K)$ of monads in $K$ to be the lax functor category $[1,K]_\ell$, which consists of lax functors, lax transformations and theirmodifications.

Spelling this out [Maranda 1966, Maranda 1968, Frei 1969 p. 269, Pumplün 1970 p 330 & 334, Coppey 1970, Street 1972 p. 150-151, review in Leinster 2004 pp. 148]:

Definition

(2-category of monads)
Let $K$ be a 2-category.

1. An object in $Mnd(K)$ is a monad $(a,t,\eta,\mu)$ in $K$;

2. a 1-morphism $(a,t) \to (b,s)$ in $Mnd(K)$ (“monad functor” or “monad transformation”)

   is given by

   1. a 1-morphism $x \colon a \to b$ in $K$

   2. a 2-morphism $\lambda \colon s x \to x t$ in $K$

   making the following diagrams commute:

   $$\array{ x & \stackrel{\eta^s x}{\to} & s x \\ \mathllap{x \eta^t} \big\downarrow & & \big\downarrow \mathrlap{\lambda} \\ x t & \overset{1}{\longrightarrow} & x t } \qquad \qquad \array{ s s x & \overset{s \lambda}{\to} & s x t & \overset{\lambda t}{\longrightarrow} & x t t \\ \mathllap{\mu^s x} \big\downarrow & & & & \big\downarrow \mathrlap{x \mu^t} \\ s x & & \overset{\lambda}{\longrightarrow} & & x t }$$

3. a 2-morphism $(x,\lambda) \Rightarrow (y, \kappa)$ in $Mnd(K)$ is given by

   • a 2-morphism $m \colon x \Rightarrow y$ in $K$

   making the following diagram commute

   $$\array{ s x & \stackrel{s m}{\to} & s y \\ \mathllap{\lambda} \downarrow & & \downarrow \mathrlap{\kappa} \\ x t & \stackrel{m t}{\to} & y t }$$

Remark

(handedness of the underlying natural transformation)
Beware that $\lambda$ in Def. is oriented oppositely to what one might expect. This need not be so but is a possible choice, see Pumplün 1970 p 334, Street 1972 pp 158.

One issue is that the functor between Kleisli categories induced by a monad morphism goes in the direction opposite of $\lambda$ as defined above (as generally for extension of scalars of module objects along a homomorphism of monoids), so that for authors who adopt the opposite of the above convention (such as Frei 1969 p. 269, Pumplün 1970 p 330, Barr & Wells 1985 §6.1 and in our Exp. below) the association of monad morphisms to functors between Kleisli catgeories is contravariant (eg. Frei 1969, Thm. 2, Barr & Wells 1985 Thm. 6.3).

Example

(transformation of monads on a fixed category)
This example is the simpler but important special case of the general Def. where the monads all act on the same fixed object – in particular the same category if $K = Cat$ (stated in this form for instance in Barr & Wells 1985 §6.1), of relevance notably for monads in computer science (where this is Moggi 1989 Def. 4.0.11) which typically all act on the same category of data types:

For a pair of monads $(\mathcal{E}, ret^{\mathcal{E}}, join^{\mathcal{E}})$, $(\mathcal{E}', ret^{\mathcal{E}'}, join^{\mathcal{E}'})$ on a fixed category $\mathbf{C}$:

$$\mathcal{E}, \mathcal{E}' \;\colon\; \mathbf{C} \longrightarrow \mathbf{C} \,,$$

a morphism between them is

• a natural transformation $trans^{\mathcal{E} \to \mathcal{E}'} \,\colon\, \mathcal{E} \to \mathcal{E}'$ between the underlying functors

such that it respects, in the evident way, the monad units

and the joins:

in that it makes these squares commute.

Remark

A monad transformation as in Exp. contravariantly induces a functor of Eilenberg-Moore categories of modales by extension of scalars [Frei 1969, Thm. 2, Barr & Wells 1985 thm. 6.3]:

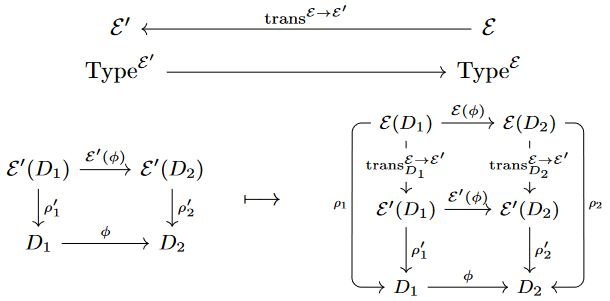
Since this extension of scalars is the identity on underlying objects, it cannot in general restrict to a functor on Kleisli categories.

However, when the monad transformation $tr \,\colon\, \mathcal{E} \to \mathcal{E}'$ is an isomorphism then $tr^\ast$ does take free modales to free modales up to isomorphism. This is seen from the following diagram:

$$\array{ \mathcal{E} \mathcal{E}(D) & \overset{ \mathcal{E}(tr_D) }{\longrightarrow} & \mathcal{E} \mathcal{E}'(D) & \overset{ trans ^{\mathcal{E} \to \mathcal{E}'} _{\mathcal{E}'(D)} }{\longrightarrow} & \mathcal{E}' \mathcal{E}'(D) \\ \Big\downarrow\mathrlap{ {}^{ join^{\mathcal{E}}_D } } && \Big\downarrow\mathrlap{ {}^{ trans^\ast join^{\mathcal{E}'}_D } } && \Big\downarrow\mathrlap{ {}^{ join^{\mathcal{E}'}_D } } \\ \mathcal{E}(D) & \underset{ \;\; trans^{\mathcal{E} \to \mathcal{E}'}_D \;\; }{\longrightarrow} & \mathcal{E}'(D) &=& \mathcal{E}'(D) }$$

Here the middle vertical morphism is the nominal image under extension of the free modale on the right along $trans^{\mathcal{E} \to \mathcal{E}'}$, but the square on the left, which commutes by assumption on $trans^{\mathcal{E} \to \mathcal{E}'}$, exhibits an isomorphism from the middle modale to the $\mathcal{E}$-free modale on the left.

Remark

(monad transfomers)
When monads are used to model computational effects in functional programming, a common concern is to combine different effects, such that previous effects are subsumed among the newly combined effects. This is formalized by “monad transformers” which are systems of morphisms of monads as in Exp. , forming a pointed endofunctor on the category $Mnd$ of all monads.

Example

The initial object in the category of monads on a fixed category $\mathbf{C}$ (Exp. ) is the identity monad.

Proof

We need to show that for every monad $\mathcal{E}$ on $\mathbf{C}$ there is a natural transformation $trans^{Id \to \mathcal{E}} \,\colon\, Id \to \mathcal{E}$ which makes, first of all, this square commute:

and this already fixes the transformation to be the monad unit of $\mathcal{E}$, as shown – such that, secondly, this square commutes:

which is the case by the unitality clause on $\mathcal{E}$, as indicated.

Algebras/modules over a monad

Given that a monad in a bicategory $\mathcal{B}$ is nothing but a monoid object in a hom-category $\mathcal{B}(a,a)$, it is natural to consider a module over this monoid: a module for a monad. This notion of module is more general than a module in a monoidal category, however, since it need not live in $\mathcal{B}(a,a)$ but can be in $\mathcal{B}(b,a)$ (for left modules) or $\mathcal{B}(a,c)$ (for right modules).

In a Cat-like bicategory, left modules over a monad are usually known as algebras over the monad. This terminology is confusing from the point of view of monads as monoids, but is justified because in Cat itself, such algebras with domain 1 are just algebras for a monad in the classical sense. Such algebras are a powerful tool to encode general algebraic structures; this is the topic of universal algebra. The algebras over a monad form its Eilenberg-Moore category, which is characterized by a universal property.

Some monads arise from operads, in which case algebras for the monad are the same as algebras for the operad. A Lawvere theory is another special sort of monad in $Cat$.

Properties

Relation between adjunctions and monads

There is a close relation between adjunctions (adjoint functors) and monads:

• Monad induced by an adjunction

• Category of adjunction-resolutions of a monad

• Semantics-Structure adjunction

Monad induced by an adjunction

Every adjunction $(L \dashv R)$ induces a monad $R \circ L$ and a comonad $L \circ R$.

(Huber 1961, §4; see eg. MacLane 1971, §VI.1 (p 134); Borceux 1994, vol. 2, prop. 4.2.1).

In detail:

Proposition

Let $(\mathcal{C},\mathcal{D},F,U,\eta,\epsilon)$ be a pair of adjoint functors ie $F \dashv U$ are adjoint functors where $F \colon \mathcal{C} \rightarrow \mathcal{D}$, $U \colon\mathcal{D} \rightarrow \mathcal{C}$, $\eta_{A}:A \rightarrow U(F(A))$ is the unit and $\epsilon_{B} \colon F(U(B)) \rightarrow B$ is the counit. Then:

• $U \circ F$ is a monad on $\mathcal{C}$, with unit $\eta$ and multiplication $U(\epsilon_{F(A)}):U(F(U(F(A)))) \rightarrow U(F(A))$.

• $F \circ U$ is a comonad on $\mathcal{D}$, with counit $\epsilon$ and comultiplication $F(\eta_{U(B)}):F(U(B)) \rightarrow F(U(F(U(B))))$.

Proof

We verify that we obtain a monad, the argument for the comonad is formally dual.

(1) We know that this diagram commutes:

By applying $U$, we obtain the first part of the unitaly of the monad:

(2) We know that this diagram commutes: By putting $B=F(A)$, we obtain the second part of the unitality of the monad:

(3) The naturality of $\epsilon$ is written, for every $f:B \rightarrow B'$:

We apply it to $f=\epsilon_{F(A)}$ and it gives:

Finally apply $U$ to this diagram to obtain:

which is exactly the associativity of the multiplication of the monad.

(4) The naturality of the multiplication $U(\epsilon_{F(A)}):U(F(U(F(A)))) \rightarrow U(F(A))$ is obtained by two whiskerings of the counit $\epsilon_{B}:U(F(B)) \rightarrow B$.

Category of adjunction-resolutions of a monad

An adjunction inducing a monad $T$ (as above) is also called a resolution of $T$.

There is in general more than one such resolution, in fact there is a category of adjunctions for a given monad whose morphisms are “comparison functors” (eg. MacLane 1971, §VI.3).

In this category:

• the initial object is the adjunction over the Kleisli category of the monad;

• the terminal object is that over the Eilenberg-Moore category of algebras, also called the monadic adjunction (recognized by monadicity theorems).

(e.g. Borceux 1994, vol. 2, prop. 4.2.2)

Semantics-structure adjunction

The above passage from adjunctions to monads and back to their monadic adjunctions constitutes itself an adjunction, sometimes called the semantics-structure adjunction.

Examples

Monads on $Set$

Many of these monads also have standard usages as monads in computer science.

Example

The free-forgetful adjunction between pointed sets and sets induces an endofunctor $(-)_* : Set \to Set$ which adds a new disjoint point. This is called the maybe monad in computer science.

Example

The free-forgetful adjunction between monoids and sets induces an endofunctor $T : Set \to Set$ defined by

$$TA := \bigsqcup_{n \ge 0} A^n$$

giving the free monoid monad. This also goes by the name list monad or Kleene-Star? in computer science. The components of the unit $\eta_A : A \to T A$ give inclusions sending each element of $A$ to the corresponding singleton list. The components of the multiplication $\mu_A : T^2 A \to T A$ are the concatenation functions, sending a list of lists to the corresponding list (Known as flattening in computer science). This monad can be defined in any monoidal category with coproducts that distribute over the monoidal product.

Example

For a fixed set of “states” $S$, the ($S \times - \dashv (-)^S$)-adjunction induces a monad $(S \times -)^S$ on $Set$ called the state monad. This is a commonly used monad in computer science. In functional programming languages such as Haskell, states can be used to model “side effects” of computations.

Example

The contravariant power set-functor is its own right adjoint, giving $\Set(A,P B) \cong \Set (B, P A)$. Note that $\hom(A, P B) = \hom(A, \hom(B,\Omega)) \cong \hom( A \times B, \Omega) = P(A \times B)$ inducing a double power set monad taking a set $A$ to $P^2 A$. The components of the unit are the principal ultrafilter functions $\eta_A \colon A \to P^2 A$ which send an element $a$ to the set of subsets of $A$ that contain $a$. The components of the multiplication $\mu_A$ is the inverse image function for the map $\eta_{P A} \colon P A \to P^3 A$; which can be painfully stated as: the function taking a set of sets of sets of subsets to the set of subsets of $A$ with the property that one of the sets of sets of subsets is the set of all sets of subsets of $A$ that include that particular subset as an element.

Replacing the two element power object $\Omega$ with any other set gives similar monads. In computer science contexts these are known as continuation monads. This construction can also be generalised for any other bi-closed monoidal category. For example there is a similar double dual monad on $\Vect_k$.

Example

function monad (also “reader monad”, cf. coreader comonad)

Example

possibility

Example

selection monad

Algebra

Example

The free-forgetful adjunction between sets and the category of $R$-modules. This induces the free $R$-module monad $R[-] : Set \to Set$. The free abelian group monad and free vector space monad are special cases.

Example

The free-forgetful adjunction between sets and the category of groups gives the free group monad $F : Set \to Set$ that sends $A$ to the set $F(A)$ of finite words in the letters $a \in A$ together with inverses $a^{-1}$.

Topology

Example

There is a forgetful functor $U : \Top \to \Set$ taking a topological space to its underlying set. It is right adjoint to the discrete space functor $D: \Set \to \Top$ taking a set to its discrete topology. There is also an adjoint pair $\beta \dashv U'$ between the category of compact Hausdorff topological spaces and the category of topological spaces, where $\beta$ is the Stone-Cech compactification. The composites of these two adjoint pairs gives a monad $\beta : \Set \to \Set$ sending a set to its underlying set of the Stone-Cech compactification of its discrete space. It is also known as the ultrafilter monad as $\beta$ can be thought of as the functor taking a set to its set of ultrafilters.

Monads in Cat

Monads are often considered in the 2-category Cat where they are given by endofunctors with a monoid structure on them. In particular, monads in Cat on Set are equivalent to the equational theories studied in universal algebra. In this context, a monad abstracts the concept of an algebraic theory (such as “group” or “ring”), giving a general notion of extra structure on an object of a category.

Classically, if $\mathbf{T}$ is an algebraic theory (e.g. the theory of groups), a $\mathbf{T}$-structure on a set tells us how to interpret various terms (e.g. $(a\cdot c)$) formed from elements of the set, subject to certain axioms (e.g. $(a\cdot (b\cdot c))=((a\cdot b)\cdot c)$). A monad collects this up into a functor $T$. For a set $X$, $T X$ is the set of all terms of the theory formed from elements of $X$, with terms identified if axioms force them to be equal. For groups, $T X$ is thus the (underlying set of the) free group of formal words $a \cdot b \cdot \cdots \cdot s$ from $X$; the fact that $T$ gives free structures turns out to be typical.

To capture the theory fully, we need to include a little more data: a natural map $\eta_X : X \to T X$ recording how each $a \in X$ gives a trivial term $a$, and a map $\mu_X:T T X \to T X$ recording how further terms built from terms are already present as terms in $T X$.

Given a monad in Cat on a category $C$, one can always produce a canonical resolution of any object of $C$.

Other examples

• Monads on posets are particularly simple (in particular, they are always idempotent). In fact, monads on power sets are extremely common throughout mathematics; they are known in less categorially-inclined circles as Moore closures, and there are many examples there.

• An internal monad on the subobject classifier of a topos $E$ is a Lawvere-Tierney topology on $E$.

• If $C$ is a category with finite limits, then a monad in the bicategory of spans in $C$ is the same thing as an internal category in $C$.

• A monad in the bicategory Prof of profunctors on a category $A$ can be identified with an identity-on-objects functor $A\to B$.

Monads in higher category theory

There is a vertical categorification of monads to (∞,1)-categories. See (∞,1)-monad.

in section 3 of

• Jacob Lurie, Noncommutative algebra (arXiv)

Related concepts

• adjunction, comonad, adjoint monad, algebra over a monad, module over a monad, monad with arities, distributive law, monoidal monad, cartesian monad

• Kleisli triple, extension system

• algebraic theory / Lawvere theory / (∞,1)-algebraic theory

• monad 2-monad/doctrine / (∞,1)-monad

  • monad (in computer science), monad (in linguistics)

  • Lawvere-Tierney topology

  • idempotent monad, strong monad

  • accessible monad

  • adjoint monad, Frobenius monad

  • finitary monad

  • enriched monad

    • additive monad

  • strong monad

  • polynomial monad

  • relative monad

  • polymonad

• operad / (∞,1)-operad

• bar construction

• monadic descent

References

The notion of (co)monads was introduced under the name “standard construction” (namely what is now thought of as their induced canonical resolution) in:

• Peter J. Huber, §2 in: Homotopy theory in general categories, Mathematische Annalen 144 (1961) 361–385 [doi:10.1007/BF01396534]

following:

• Roger Godement, Appendix of: Topologie algébrique et theorie des faisceaux, Actualités Sci. Ind. 1252, Hermann, Paris (1958) [webpage, pdf]

  (where the monad laws appear on p. 272 as part of the structure of the induced canonical resolution, called there the “fundamental construction”).

In the early category theory-literature monads were called triples, referring to the fact that (just as for monoids) their data-structure is that of triples consisting of: (1.) the underlying category, (2.) a binary operation and (3.) a unit operation:

• H. Applegate, M. Barr, J. Beck, F. W. Lawvere, F. E. J. Linton, E. Manes, M. Tierney, F. Ulmer: Seminar on Triples and Categorical Homology Theory, ETH 1966/67, edited by Beno Eckmann and Myles Tierney, LNM 80, Springer (1969), reprinted as: Reprints in Theory and Applications of Categories 18 (2008) 1-303 [TAC:18, pdf]

The modern terminology “monad” (and the definition in the generality internal to any bicategory) is (cf. Barr 2009) due to:

• Jean Bénabou, §5.4 in: Introduction to Bicategories, Lecture Notes in Mathematics 47 Springer (1967) 1-77 [doi:10.1007/BFb0074299]

Further historical comments:

• Martin Hyland, John Power, The Category Theoretic Understanding of Universal Algebra: Lawvere Theories and Monads, Electronic Notes in Theor. Comp. Sci. 172 (2007) 437-458 [doi:10.1016/j.entcs.2007.02.019, preprint]

• Michael Barr, Re: Where does the term monad come from? (April 1, 2009) [cat-dist:09-4, txt, jpg]

• Ross Street, Re: monads (April 4, 2009) [cat-dist:09-4, txt, jpg]

Further original texts:

• Jean-Marie Maranda, On Fundamental Constructions and Adjoint Functors, Canadian Mathematical Bulletin 9 5 (1966) 581-591 [doi:10.4153/CMB-1966-072-9]

• Jean-Marie Maranda, Sur les Proprietes Universelles des Foncteurs Adjoints, In: Études sur les Groupes abéliens / Studies on Abelian Groups Springer (1968) [doi:10.1007/978-3-642-46146-0_16]

• Fred Linton, An outline of functorial semantics, in Seminar on Triples and Categorical Homology Theory, Lecture Notes in Mathematics 80, Springer (1969) 7-52 [doi:10.1007/BFb0083080]

• Fred Linton, Applied functorial semantics, in Seminar on Triples and Categorical Homology Theory, Lecture Notes in Mathematics 80, Springer (1969) 53-74 [doi:10.1007/BFb0083080]

• Armin Frei, Some remarks on triples, Mathematische Zeitschrift 109 (1969) 269–272 [doi:10.1007/BF01110118]

• Dieter Pumplün, Eine Bemerkung über Monaden und adjungierte Funktoren, Mathematische Annalen 185 (1970) 329-337 [eudml:161964, pdf]

• Laurent Coppey, Morphismes et comorphismes de cotriples, C. R. Acad. Sc. Paris 271 (1970), [ark:12148/bpt6k5619186c/f27]

• Saunders MacLane, Ch. VI of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (1971) [doi:10.1007/978-1-4757-4721-8]

• Jean Bénabou, Les Triples, Séminaire de mathématiquepure pure 26, Université de Louvain (1972) [pdf]

• Ross Street, The formal theory of monads, Journal of Pure and Applied Algebra 2 2 (1972) 149-168 [doi:10.1016/0022-4049(72)90019-9]

• Stephen Lack, Ross Street, The formal theory of monads II, Journal of Pure and Applied Algebra

  175 1–3 (2002) 243-265 [doi:10.1016/S0022-4049(02)00137-8]

• Michael Barr, Charles Wells, Chapter 3 of: Toposes, Triples, and Theories, Grundlehren der math. Wissenschaften 278, Springer (1985), Reprints in Theory and Applications of Categories 12 (2005) 1-287 [tac:tr12]

Further textbook accounts:

• Francis Borceux, Ch. 4 “Monads” in: Handbook of Categorical Algebra vol. 2, Encyclopedia of Mathematics and its Applications 50, Cambridge University Press (1994)

Expositions:

• The Catsters, Monads, short video lectures (2007) [1:YT, 2:YT, 3:YT, 3A:YT, 4:YT, 5/6:YT]

• John Baez, Universal Algebra and Diagrammatic Reasoning (Introductory slides).

• Emily Riehl, p. 154 of: Category Theory in Context (2017)

• Paolo Perrone, Notes on Category Theory with examples from basic mathematics, Chapter 5. (arXiv)

More on the relation to universal algebra:

• Martin Hyland and John Power, The category theoretic understanding of universal algebra: Lawvere theories and monads (pdf).

• Anthony Voutas, The basic theory of monads and their connection to universal algebra, (2012) [pdf, pdf]

An elementary proof of the equivalence between infinitary Lawvere theories and monads on the category of sets is given in Appendix A of

• Martin Brandenburg, Large limit sketches and topological space objects [arXiv:2106.11115]

In higher category theory:

• T. M. Fiore, N. Gambino, J. Kock, Monads in double categories, arxiv/1006.0797

• Gabriella Böhm, Stephen Lack, Ross Street, Weak bimonads, arxiv/1002.4493