nLab Hegelian taco
Context
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Contents
Idea
The Hegelian taco is food for thought from William Lawvere's kitchen. More concretely, it is an eight-element graphic monoid that intends to capture diagrammatically the essence of a certain configuration of stacking subcategories of a given category that occurs in Lawvere’s mathematical rendering of Hegel's dialectical logic.
Construction
The situation we start with is the following sequence of functors and adjunctions
Here every column of arrows, numbered descendingly from left to right describes an essential localization with fully faithful. These yield a pair of idempotent adjoint modalities whose functor parts are . Importantly, all the junctures vanish in the sense , since this composition corresponds to the inclusion of a subcategory followed by a projection back to the subcategory.
If we compose the functors appropriately we obtain four such adjunctions on which correspond to reflective and coreflective embeddings of descending complexity of the chain of subcategories :
The respective endofunctors on are defined as
They are supposed to provide the elements of the taco monoid . So far we have seven of them including . The eighth will show up when we set up the multiplication table, so let’s do that:
-
The first case we consider is when we multiply two elements that appear on the same side of like e.g. and that are both left adjoints: here is of lower complexity than as it corresponds to a smaller subcategory, namely . When we multiply, or , at the junctures will arise in both cases which is just the ‘splitting’ of and therefore cancels and we retain the ‘lower’ functor . This happens in all cases where we multiply elements of the same ‘laterality’: the lower element absorbs the higher. This can be viewed as capturing the facet of ‘preservation’ present in Hegelian Aufhebung: the higher concept is just when restricted to the smaller subcategory.
-
Next we come to the cases where we multiply elements of opposite laterality of the same complexity e.g. like and . Here the factors arising at the junctures cancel again and in these cases we retain always the left factor e.g. and . One can view this as capturing the destructive nature of a Hegelian ‘dialogue’: ‘objecting’ to ‘proposal’ cancels and vice versa.
-
Now we come to the cases that express the constructive-progressive nature of Hegelian dialectic: namely, when we multiply elements of opposite laterality of different complexity e.g. like and . Let us concentrate on the case that the difference in complexity is just a single step. First we note, that the dialogue situation is conceived of as being asymmetrical: the right adjoint acts as proponent whereas the left adjoint opponent contradicts. So in this particular formalization, the proponent tries to assimilate the opponent’s view but not vice versa: in a ‘situation’ where the ‘proponent’ is faced with ‘opposition’ , she might just insist but she might as well try to take into account i.e. change her view to , with the ‘higher order refinement’ now ‘accepting’ in the sense that . This relation that not only factors through but through , is called resolution of (the contradiction of) level by level (For further details see at Aufhebung). It gives us the equations , , and (trivially) for the three steps of sublations.
As we’ve said, the situation is handled somewhat asymmetrical in that we systematically care only that we can incorporate the negative view into the positive ‘right adjoint’ view but not the reverse. For the reverse cases and we stipulate: 1) (this would hold, as often occurs in the applications, that there is an additional left adjoint since in that case as a composition of right adjoints would preserve the limit ) and 2.) which give us our eighth element!
So much for the ‘philosophical’ motivation behind the multiplication table that is going to follow in the next section!
Some might feel more comfortable with the information that, technically, the taco monoid intends to abstract the relations occuring between three essential localizations such that, starting from , a higher localization resolves the preceding lower level in the sense that .
Definition
The Hegelian taco is the monoid on the set with the following multiplication table:
Properties
is a graphic monoid i.e. for all we have , in particular all elements are idempotent.
The poset of left ideals in is:
They parametrize the essential localizations of the associated presheaf topos . The dimension theory that comes with this is detailed in Kelly-Lawvere (1989) and Lawvere (1989). In the present case, the result is that is three-dimensional.
This motivates also the culinary allusion in the name, where the essential localization corresponding to is seen as providing the two-dimensional ‘sides’ via its reflective and coreflective inclusions around the three-dimensional ‘filling’ . Of course, the one-dimensional pieces corresponding to find their place on the sandwich as well. The following picture of the taco appears in Lawvere (1989), where further details may be found.
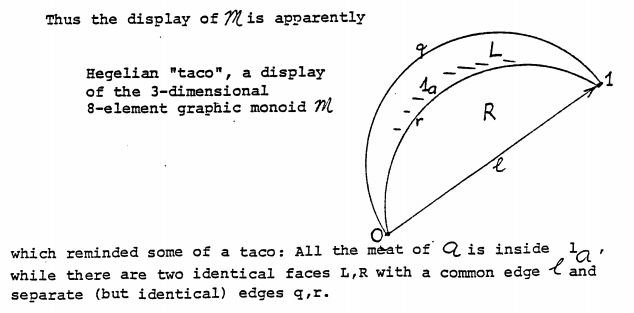
Let us point out that can be viewed as ‘cubical generalization’ of the three-element graphic monoid that underlies the (one-dimensional) presheaf topos of reflexive graphs (for a detailed description of and its topos see at graphic category). encapsulates the diagram
that expresses abstractly a cylinder configuration corresponding to ‘opposition’ or ‘conflict’ from the dialogical point of view.1
Remarks
-
If one takes into account also the natural transformations arising from the adjunctions one can turn into a finite monoidal category.
-
The main reference for the taco is Lawvere (1989, pp.70-73). It is mentioned in Lawvere (1991,2003) as well.
Related entries
-
graphic topos?
References
-
G. M. Kelly, F. W. Lawvere, On the complete lattice of essential localizations , Bull. Soc. Math. de Belgique XLI (1989) 289-319 [pdf]
-
F. W. Lawvere, Display of graphics and their applications, as exemplified by 2-categories and the Hegelian “taco” Proceedings of the first international conference on algebraic methodology and software technology University of Iowa, May 22-24 1989, Iowa City, pp. 51-74. (pdf)
-
F. W. Lawvere, More on graphic toposes, Cah. Top. Géom. Diff. Cat. XXXII no. 1 (1991) pp.5-10. (pdf)
-
F. W. Lawvere, Unity and identity of opposites in calculus and physics , App. Cat. Struc 4 (1996) pp.167-174. (pdf)
-
F. W. Lawvere, Linearization of graphic toposes via Coxeter groups, JPAA 168 (2002) pp. 425-436. (pdf)
-
Lawvere expands a bit on the diagrammatic perspective on in Lawvere (1996). ↩
Last revised on March 27, 2023 at 07:21:33. See the history of this page for a list of all contributions to it.