nLab functor

Contents

Context

Category theory

Idea

A functor is a homomorphism of categories.
A functor between small categories is a homomorphism of the underlying graphs that respects the composition of edges.

So, for $C$ , $D$ two categories, a functor $F \colon C \to D$ consists of

a component-function of the classes of objects;

$F_0 \colon Obj(C) \to Obj(D)$

a component-function of sets of morphisms

$F_1 \colon Mor(C) \to Mor(D)$

or equivalently:

for each pair $x,y \in Obj(C)$ of objects, a component-function

(1) $F_{x,y} \;\colon\; C(x,y) \xrightarrow{\;\;} D(F(x), F(y))$

between hom-sets;

such that:

it respects source and target of morphisms: $F_1$ coincides with $F_0$ on source and target objects;
it respects identity morphisms: $F(id_X) = id_{F(X)}$ ;
it respects composition: the image of the composite of two morphisms under $F$ is the composite of their images.

These last two properties are the decisive ones of a functor; they are called the functoriality conditions. These are a direct generalization of the notion of homomorphism (of monoids, groups, algebras, etc.) to the case that there are more objects. As a slogan:

The notion of functor is a horizontal categorification of that of homomorphism.

Definition

External definition

A functor $F$ from a category $C$ to a category $D$ is a map sending each object $x \in C$ to an object $F(x) \in D$ and each morphism $f : x \to y$ in $C$ to morphism $F(f) : F(x) \to F(y)$ in $D$ , such that

$F$ preserves composition: $F(g\circ f) = F(g)\circ F(f)$ whenever the left-hand side is well-defined,
$F$ preserves identity morphisms: for each object $x \in C$ , $F(1_x) = 1_{F(x)}$ .

Or equivalently, since compositions $g f = g\circ f$ (commuting triangles) and identities $1_x$ (commuting loops) are both simple commuting diagrams, we can combine the above conditions to the single statement

$F$ preserves commuting diagrams.

Given morphisms $f \colon X\to Y$ , $g \colon Y\to Z$ , and $h \colon X\to Z$ , declaring the triangle commutes amounts to declaring

h = g\circ f.

In this case, for $F:C\to D$ to preserve the commutative triangle means

F(h) = F(g)\circ F(f)

as depicted below

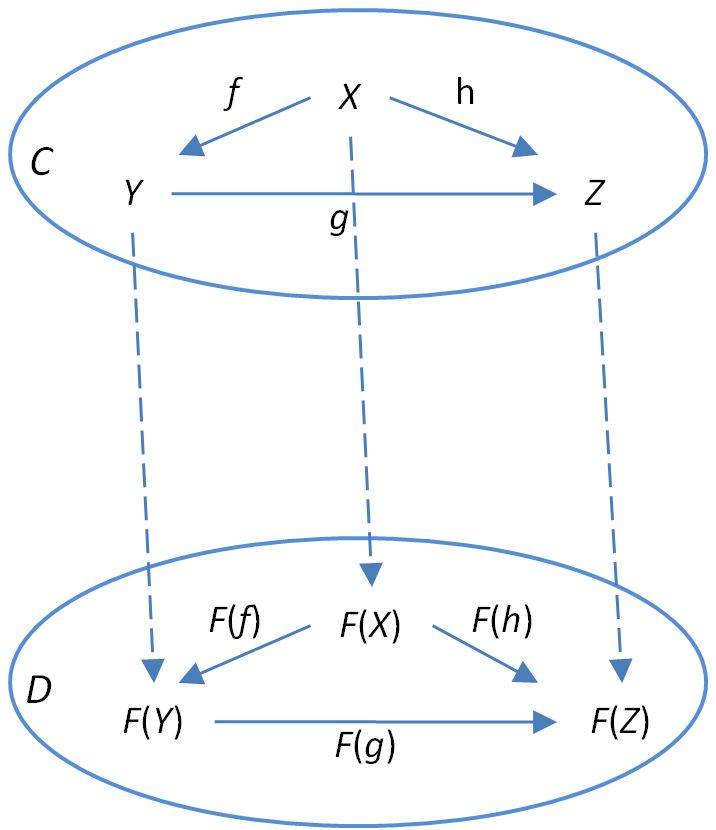
Preserving commuting triangles means $F$ preserves compositions.

Given morphisms $f:X\to Y$ , $g:Y\to Z$ , and $h:Z\to X$ , declaring the loop commutes amounts to declaring

1_X = h\circ g\circ f.

In this case, for $F:C\to D$ to preserve the commutative loop means

F(1_X) = F(h)\circ F(g)\circ F(f)

as depicted below

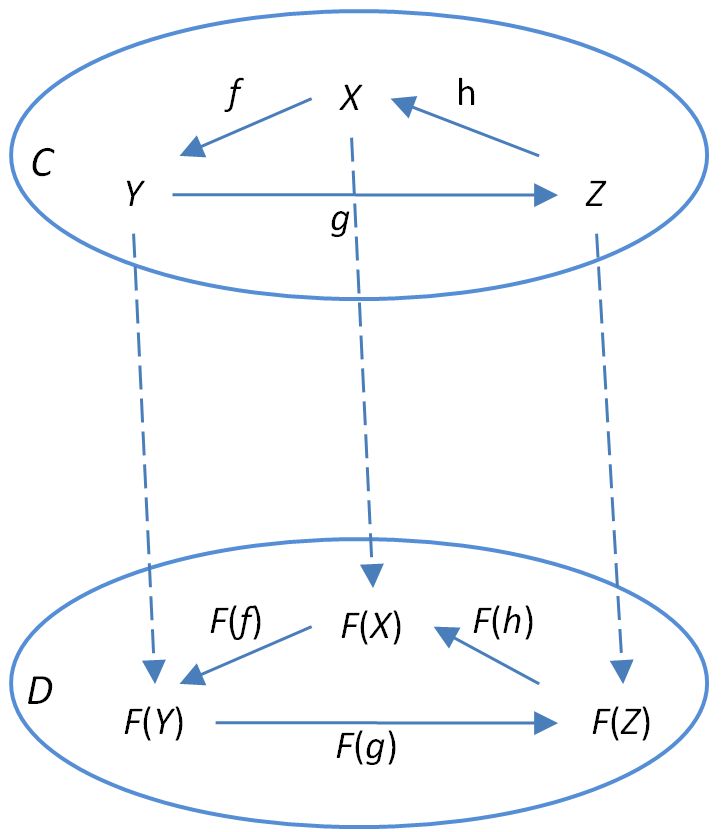
However, it means more than that. Since any commutative loop is equal to the identity morphism, we must also have

1_{F(X)} = F(h)\circ F(g)\circ F(f)

implying

F(1_X) = 1_{F(X)}.

Preserving commuting loops means $F$ preserves identity morphisms.

Another equivalent way to say this is that a functor $F : C \to D$ is precisely a morphism of simplicial sets $N(F) : N(C) \to N(D)$ between the nerves of these categories

the objects of $C$ and $D$ are the 0-cells of $N(C)$ and $N(D)$ , so $N(F)_0 : N(F)_0 \to N(F)_0$ maps objects of $C$ to objects of $D$ ;
the morphisms of $C$ and $D$ are the 1-cells of $N(C)$ and $N(D)$ , so $N(F)_1 : N(F)_1 \to N(F)_1$ maps morphisms of $C$ to objects of $D$ ;
the identity morphisms of $C$ and $D$ are the degenerate 1-cells of $N(C)$ and $N(D)$ , so the fact that $N(F)$ respects degeneracy maps means that $F$ respects identities;
the commuting triangles of $C$ and $D$ are the 2-cells of $N(C)$ and $N(D)$ , so the fact that $N(F)$ maps 2-cells to 2-cells means that it respects commuting triangles, hence that it respects composition.

See nerve for more details on this.

The functors between two categories $C$ and $D$ form themselves a category, the functor category $[C,D]$ , whose morphisms are natural transformations. Equipped with these functor categories as hom-objects, we have a $2$ -category Cat of categories, functors and natural transformations. In other words, functors are morphisms in $Cat$ .

Internal definition

If $C$ and $D$ are internal categories in some ambient category $A$ , then an internal functor $F : C \to D$ is

a morphism of objects $F_0 : C_0 \to D_0$ in $A$ ;
a morphisms of morphisms $F_1 : C_1 \to D_1$ in $A$ ;
such that the following diagrams commute
- respect for the source map: $\array{ C_1 &\stackrel{f_1}{\to}& D_1 \\ \downarrow^s && \downarrow^s \\ C_0 &\stackrel{f_0}{\to}& D_0 }$ ;
- respect for the target map: $\array{ C_1 &\stackrel{f_1}{\to}& D_1 \\ \downarrow^t && \downarrow^t \\ C_0 &\stackrel{f_0}{\to}& D_0 }$ ;
- respect for identities $\array{ C_0 &\stackrel{f_0}{\to}& D_0 \\ \downarrow^i && \downarrow^i \\ C_1 &\stackrel{f_1}{\to}& D_1 }$ ;
- respect for composition $\array{ C_1 \times_{t,s} C_1 &\stackrel{f_1\times_{t,s} f_1}{\to}& D_1 \times_{t,s} D_1 \\ \downarrow^{\circ} && \downarrow^{\circ} \\ C_1 &\stackrel{f_1}{\to}& D_1 }$ .

This reproduces the external definition of functors above for small categories, which are categories internal to Set

In many cases, this notion is too restrictive, and we should use internal anafunctors instead.

Enriched definition

In enriched category theory a functor maps not hom-sets but the given hom-objects to each other, in a way that respects their composition. This is described at

enriched functor.

Profunctors

A generalization of the notion of enriched functor is the notion of profunctor.

Higher categorical functors

In higher category theory there are corresponding higher notions of functor, such as

2-functor
(∞,1)-functor
See also an informal discussion about an experimental alternative definition of functor.

In homotopy type theory

Note: the HoTT book calls a category a “precategory” and a univalent category a “category”, but here we shall refer to the standard terminology of “category” and “univalent category” respectively.

The definition of functor in homotopy type theory is a straightforward translation of the ordinary one. However, the notion of univalent category allows us to construct some such functors that in classical mathematics would require either the axiom of choice or the use of anafunctors.

Let $A$ and $B$ be categories. Informally, a functor $F : A \to B$ consists of

A function $F_0 : A_0 \to B_0$
For each $a,b:A$ , a function $F_{a,b}:hom_A(a,b) \to hom_B(F a,F b)$ , generally also denoted $F$ .
For each $a:A$ , we have $F(1_a)=1_{F a}$ .
For each $a,b,c: A$ and $f:hom_A(a,b)$ and $g:hom_A(b,c)$ , we have

F(g \circ f) = F g \circ F f

Formally, the type of functors from $A$ to $B$ is

Func(A,B) \coloneqq \sum_{F_0:A_0\to B_0} \sum_{F:\prod_{a,b:A} hom_A(a,b) \to \hom_B(F a,F b)} \Big(\prod_{a:A} F(1_a) = 1_{F a}\Big) \times \Big( \prod_{a,b,c:A} \prod_{f:\hom_A(a,b)} \prod_{g:\hom_A(b,c)} F(g \circ f) = F g \circ F f\Big)

A formal definition in Coq can be found in Ahrens-Kapulkin-Shulman 13.

Properties

These properties come from the HoTT book.

By induction on identity, a functor also preserves $idtoiso$ (See category).

Composition of functors

For functors $F:A\to B$ and $G:B \to C$ , their composite $G \circ F : A \to C$ is given by

The composite $(G_0 \circ F_0): A_0 \to C_0$
For each $a,b:A$ , the composite
$(G_{F a, F b} \circ F_{a,b}):hom_A(a,b)\to hom_C(G F a, G F b)$

Lemma 9.2.9 in HoTT book

Composition of functors is associative $H(G F)=(H G)F$ .

Proof: Since composition of functions is associative, this follows immediately for the actions on objects and on homs. And since hom-sets are sets, the rest of the data is automatic. $\square$

Lemma 9.2.10 in HoTT book

Lemma 9.2.9 is coherent, i.e. the following pentagon of equalities commutes:

\array{ && (K H)(G F) \\ & \nearrow && \searrow \\ ((K H) G) F && && K (H (G F)) \\ \downarrow && && \uparrow \\ (K(H G)) F && \longrightarrow && K( (H G) F) }

Types of functors

Specific types of functors are important in applications. See for instance

And for more background on this see stuff, structure, property.

Examples

Morphisms of monoids and groups

For $A,B$ monoids or $G, H$ groups, let $\mathbf{B}A, \mathbf{B}B$ , $\mathbf{B}G$ , $\mathbf{B}H$ be the corresponding one-object categories (as described at delooping). Then functors

\mathbf{B}A \to \mathbf{B}B

are canonically in bijection with monoid homomorphisms $A \to B$ and accordingly functors

\mathbf{B}G \to \mathbf{B}H

are canonically in bijection with group homomorphisms $G \to H$ .

Representations

With $\mathbf{B}G$ as above, functors on $\mathbf{B}G$ with values in Vect are the same as linear representations of the group $G$ . In fact, we have a canonical isomorphism of categories

Funct(\mathbf{B}G, Vect) \simeq Rep(G)

of the functor category with the representation category.

Linear Maps

Let $\mathbf{B} End(U)$ and $\mathbf{B} End(V)$ be one-object categories whose objects are each finite-dimensional vector space and whose morphisms are all of the linear endomorphisms on that space, i.e. one-object full subcategories of $Fin Vect$ .

Left Inverses

If the linear map $F:U\to V$ has a left inverse, i.e.

F^*\circ F = 1_U,

where $F^*$ is the preimage, then we can construct a functor

F_*:\mathbf{B} End(U)\to\mathbf{B} End(V)

by defining its action on objects by

F_*(U) = F_* U

where $F_*$ on the right-hand side is the image and its action on endomorphisms by

F_*(f) = F f F^*.

Composition follows immediately

F_*(f g) = F f g F^* = F f F^* F g F^* = F_*(f) F_*(g).

Identity morphisms are preserved since for any vector $y$ in $F_*U\subset V$ , then

y = F x

for some vector $x$ in $U$ and we have

F_*(1_U)y = F\circ F^* y = F\circ F^*\circ F x = F x = y

so that

F_*(1_U) = 1_{F_*(U)}

as required. Hence, $F_*$ is a functor.

Right Inverses

If the linear map $F:U\to V$ has a right inverse, i.e.

F\circ F^* = 1_V,

where $F^*$ is the preimage, then we can construct a functor

F^*:\mathbf{B} End(V)\to\mathbf{B} End(U)

by defining its action on objects by

F^*(V) = F^*V

where $F^*$ on the right-hand side is preimage, and its action on endomorphisms by

F^*(f) = F^* f F.

Composition follows immediately

F^*(f g) = F^* f g F = F^* f F F^* g F = F^*(f) F^*(g).

Identity morphisms are preserved since for any vector $x$ in $F^*V\subset U$ , then

x = F^*y

for some vector $y$ in $V$ and we have

F^*(1_V)x = F^*\circ F x = F^*\circ F \circ F^* y = F^* y = x

so that

F^*(1_V) = 1_{F^*(V)}

as required. Hence, $F^*$ is a functor.

Presheaves

Functors $F : C \to Set$ with values in Set are also called presheaves. As such one calls them presheaves on the opposite category $C^{op}$ of $C$ . See presheaf for more on this.

Functors and generalized elements

For $C$ a category, and $X \in C$ an object, and $U$ any other object, a morphism $x : U \to X$ may be regarded as a generalized element of $X$ , written $x \in X$ (For this language applied to the category Set of sets see ETCS. For the general case see type theory).

The set of generalized elements of an object $X \in C$ is thus the union of hom-sets $\coprod_{U \in C} Hom_C(U,X)$ .

While a morphism $f : X \to Y$ in an arbitrary category $C$ need not at all come to us as a function of sets, it always induces a function of sets of generalized elements : it sends the generalized element $x : U \to X$ of $X$ to the generalized element

f(x) : U \stackrel{x}{\to} X \stackrel{f}{\to} Y

of $Y$ , using the composition of the morphism $f$ with the morphism $x$ in $C$ .

In terms of this notation, the functoriality condition on a functor $F : C \to D$ , which is

F(U \stackrel{x}{\to} X \stackrel{f}{\to} Y) = F(U) \stackrel{F(x)}{\to} F(X) \stackrel{F(f)}{\to} F(Y)

appears as

F(f(x)) = F(f)(F(x)) \,.

This can be illustrated in the following diagram

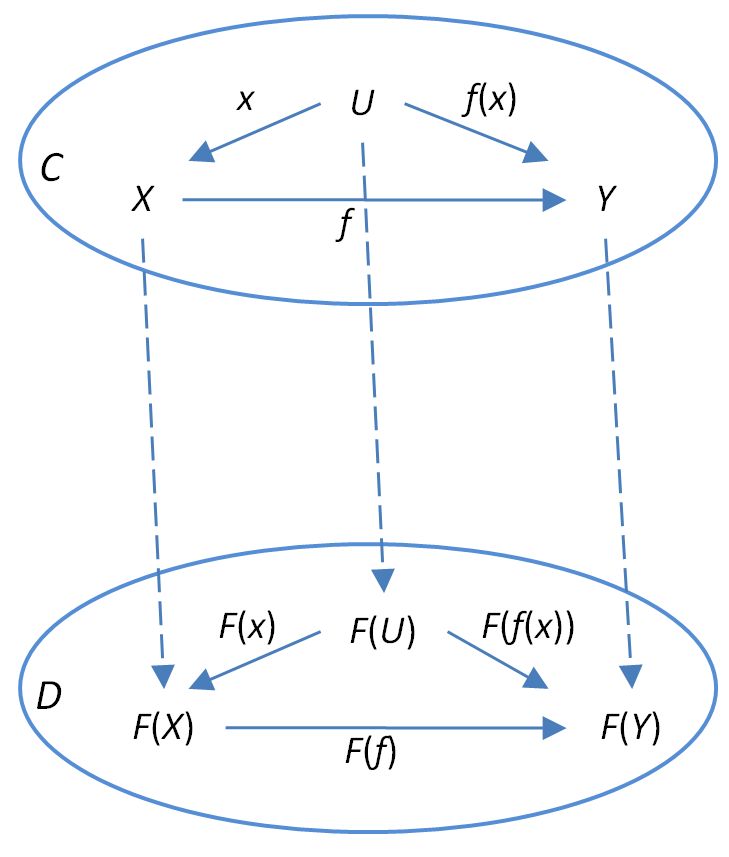
which provides an alternative expression of the functoriality condition as simply a statement that commuting diagrams in $C$ map to commuting diagrams in $D$ .

Related concepts

endofunctor
bifunctor
profunctor
multifunctor
function
functor
- endofunctor
- polynomial functor
2-functor / pseudofunctor
- monoidal functor
n-functor
(∞,1)-functor
(∞,n)-functor

basic properties of…

References

Textbook accounts:

Saunders MacLane, §I.3 of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (1971, second ed. 1997) [doi:10.1007/978-1-4757-4721-8]
Francis Borceux, Section 1.2 in: Handbook of Categorical Algebra Vol. 1: Basic Category Theory [doi:10.1017/CBO9780511525858]