nLab logic gate
Context
Computation
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Contents
Idea
Broadly, a logic gate is a function of tuples of truth values, hence a map between cartesian products of Booleans .
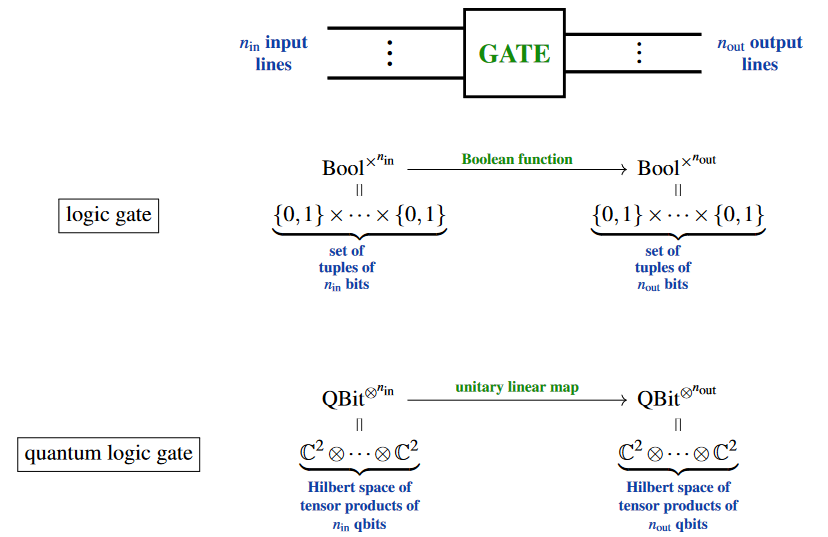
Specifically, one calls such a function a logic gate if it is thought of as potentially implemented as a basic operation performed by a computing machine – in which case the truth values are also called bits.
As such, typical logic gates are Boolean functions between a small number of bits, with more complicated such functions thought as obtained by composing a given set of logic gates into logic circuits.
Analogously there are quantum logic gates compiled into quantum circuits.
Examples
A list of some basic logic and gates and their reversible and quantum logic gate versions:
NOT:
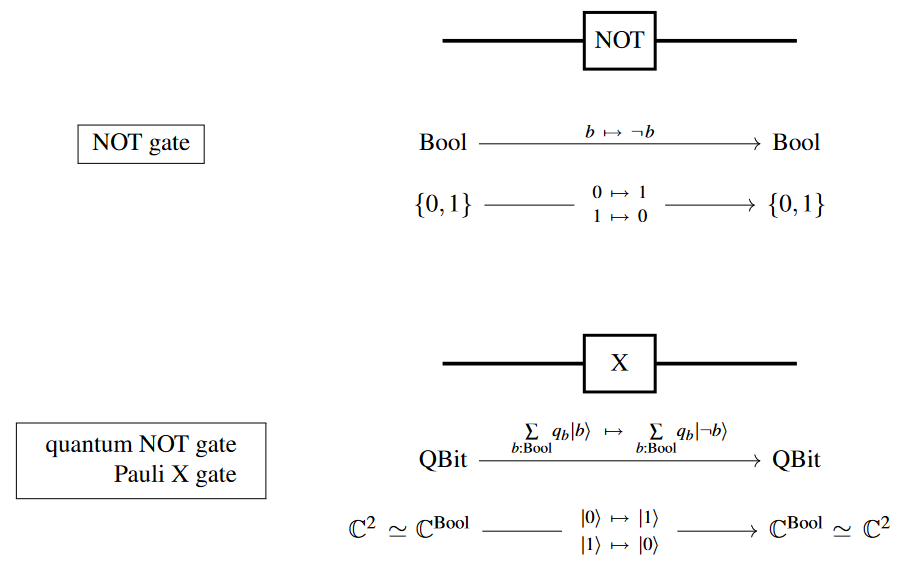
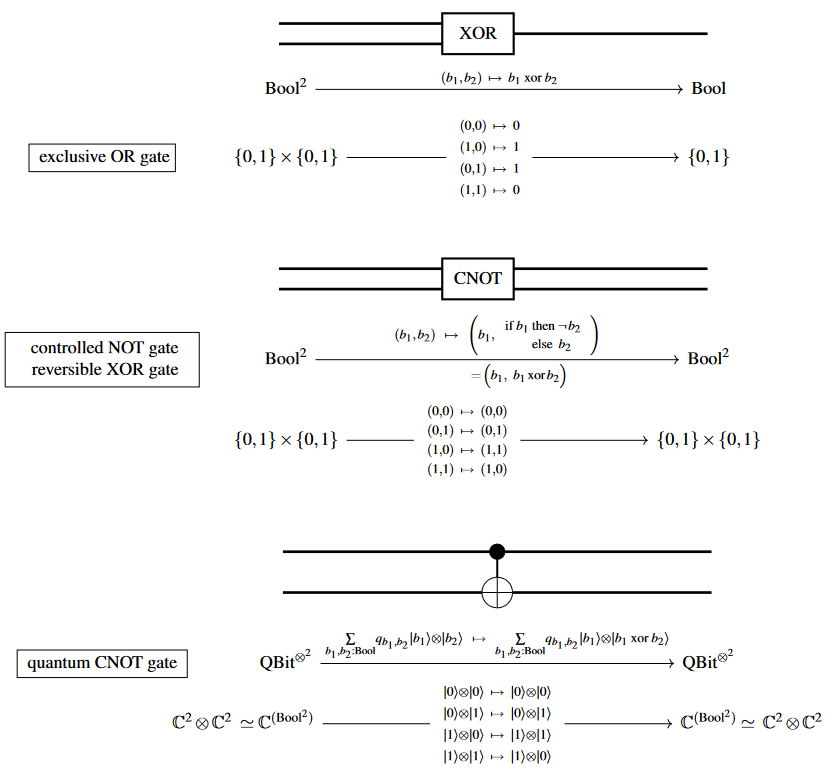
AND:
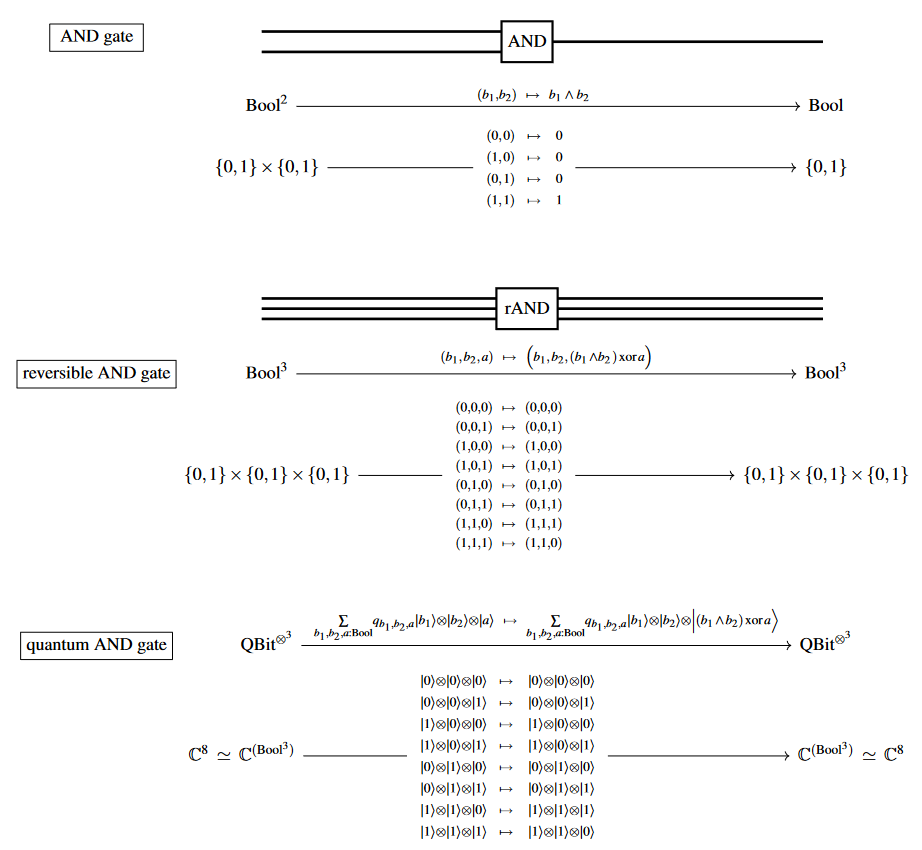
(…)
Related concepts
References
Textbook accounts:
-
Jan Friso Groote, Rolf Morel, Julien Schmaltz, Adam Watkins, Logic Gates, Circuits, Processors, Compilers and Computers, Springer (2021) [doi:10.1007/978-3-030-68553-9]
-
John Bird, Chapter 7 of: Bird’s Higher Engineering Mathematics, Routledge (2021) [ISBN:9781003124221]
See also:
- Wikipedia, Logic gate
Last revised on February 24, 2023 at 07:51:38. See the history of this page for a list of all contributions to it.