nLab computation
Context
Computability
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Deduction and Induction
Foundations
The basis of it all
Set theory
- fundamentals of set theory
- material set theory
- presentations of set theory
- structuralism in set theory
- class-set theory
- constructive set theory
- algebraic set theory
Foundational axioms
-
basic constructions:
-
strong axioms
-
further
Removing axioms
Contents
Idea
A program. A construction of a term of some type. The topic of computability theory.
Related concepts
| type I computability | type II computability | |
|---|---|---|
| typical domain | natural numbers | Baire space of infinite sequences |
| computable functions | partial recursive function | computable function (analysis) |
| type of computable mathematics | recursive mathematics | computable analysis, Type Two Theory of Effectivity |
| type of realizability | number realizability | function realizability |
| partial combinatory algebra | Kleene's first partial combinatory algebra | Kleene's second partial combinatory algebra |
References
General
On the theory of computation and introducing the notion of denotational semantics of programming languages:
-
Dana S. Scott, Outline of a mathematical theory of computation, in: Proceedings of the Fourth Annual Princeton Conference on Information Sciences and Systems (1970) 169–176. [pdf, pdf]
-
Dana S. Scott, Christopher Strachey, Toward a Mathematical Semantics for Computer Languages, Oxford University Computing Laboratory, Technical Monograph PRG-6 (1971) [pdf, pdf]
Textbook accounts:
- Michael Sipser, Introduction to the Theory Of Computation, 3rd ed: Cengage Learning (2012) [ISBN:978-1-133-18779-0,pdf, pdf]
An account with focus on programming languages:
- Robert Harper, Practical Foundations for Programming Languages, Cambridge University Press (2016) [ISBN:9781107150300, pdf]
An account going from classical computation to quantum computation:
- Alexei Y. Kitaev, A. H. Shen, M. N. Vyalyi, Classical and Quantum Computation, Graduate Studies in Mathematics 47 (2002) [doi:10.1090/gsm/047]
On computation in relation to physics (cf. computable physics):
-
Hector Zenil (ed.): A Computable Universe – Understanding and Exploring Nature as Computation, World Scientific (2012) [doi:10.1142/8306]
foreword by Roger Penrose [arXiv:1205.5823]
introduction by Hector Zenil [arXiv:1206.0376]
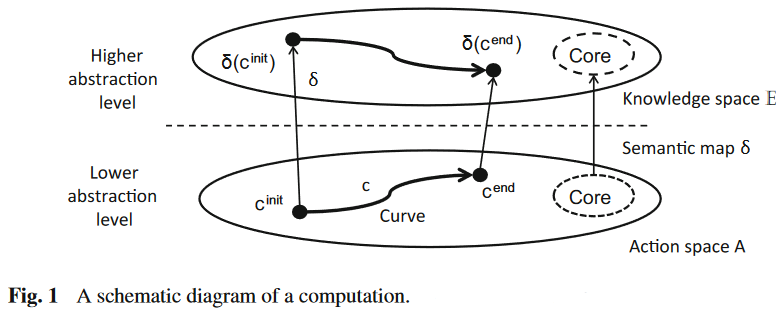
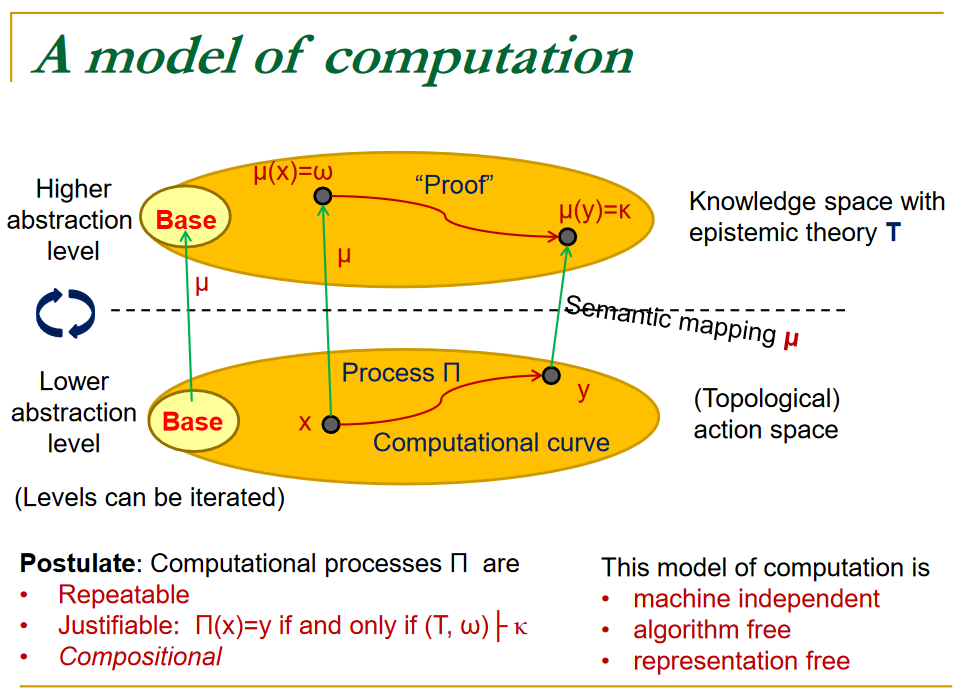
As path lifting
A conceptualization of computation as something at least close to path-lifting and/or as functors between path groupoids of topological spaces (a “semantical mapping” from an “action space” parameterizing the possible computing instructions to a “knowledge space” expressing their executions):
- Jan van Leeuwen, The Philosophy of Computation, p. xix-xxx in: Proceedings of IIT.SRC 2015 – Student Research Conference Bratislava (2015) [full proceedings: pdf, web; article: pdf; slides: pdf]
-
Jan van Leeuwen, Jiří Wiedermann: What is Computation – An Epistemic Approach, p. 1-13 in Proceedings of SOFSEM 2015: Theory and Practice of Computer Science, Lecture Notes in Computer Science 8939, Springer (2015) [doi:10.1007/978-3-662-46078-8, talk slides: pdf]
-
Jan van Leeuwen, Jiří Wiedermann: Knowledge, Representation and the Dynamics of Computation, pp. 69-89 in: Representation and Reality in Humans, Other Living Organisms and Intelligent Machines, Studies in Applied Philosophy, Epistemology and Rational Ethics 28, Springer (2017) [doi:10.1007/978-3-319-43784-2_5, pdf]
- Jan van Leeuwen, Jiří Wiedermann, Understanding Computation – A General Theory of Computational Processes, Technical Report UU-CS-2019-012, Utrecht University (2019) [dspace:1874/390075, pdf, pdf]
Related discussion for quantum computation, with quantum circuits regarded as paths:
-
Paolo Zanardi, Mario Rasetti, p. 1 of: Holonomic Quantum Computation, Phys. Lett. A 264 (1999) 94-99 [doi:10.1016/S0375-9601(99)00803-8, arXiv:quant-ph/9904011]
-
Michael A. Nielsen, Mark R. Dowling, Mile Gu, Andrew C. Doherty, Quantum Computation as Geometry, Science, 311 5764 (2006) 1133-1135 [doi:10.1126/science.1121541, arXiv:quant-ph/0603161]
-
Mark R. Dowling, Michael A. Nielsen, The geometry of quantum computation, Quantum Information & Computation 8 10 (2008) 861–899 [doi:10.5555/2016985.2016986, arXiv:quant-ph/0701004]
-
David Jaz Myers, Hisham Sati Urs Schreiber, §3 in: Topological Quantum Gates in Homotopy Type Theory [arXiv:2303.02382]
Last revised on November 1, 2024 at 07:01:38. See the history of this page for a list of all contributions to it.