nLab quantum logic gate

Idea

Analogously to how a classical logic gate is a function between (finite) sets of tuples of bits (truth values), so a quantum logic gate is a (unitary) linear operator on (finite-dimensional) Hilbert spaces of tensor products of qbits:

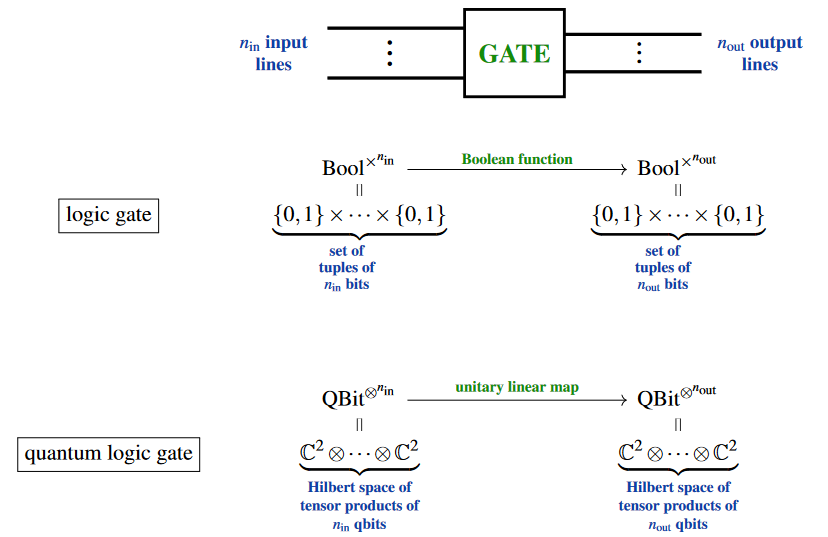
Specifically, one calls such a linear map a quantum gate if it is thought of as potentially implemented as a basic operation performed by a quantum computing machine.

As such, typical quantum logic gates operate on a small number of qbits, with more complicated such linear maps obtained by composing a given set of quantum logic gates into quantum logic circuits. Such compilation is hence one model of quantum computation.

Examples

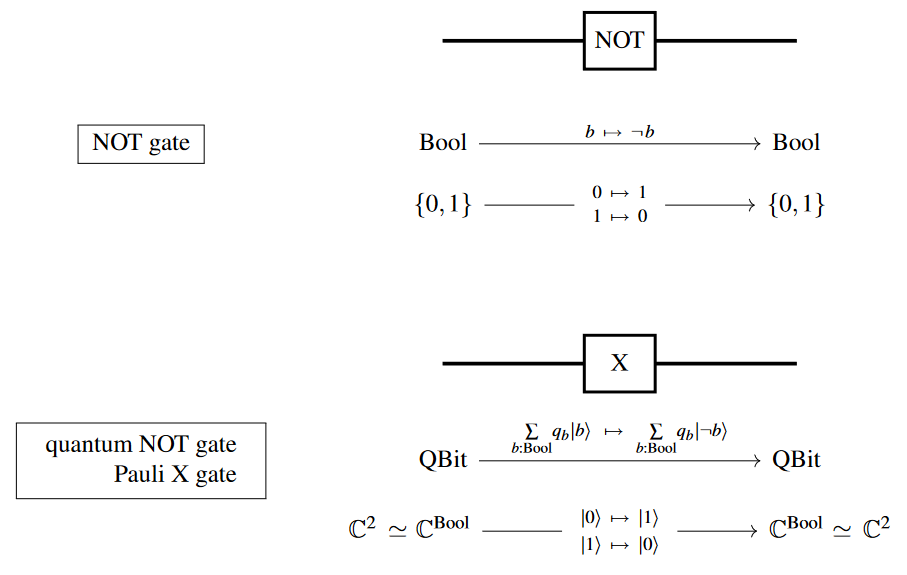
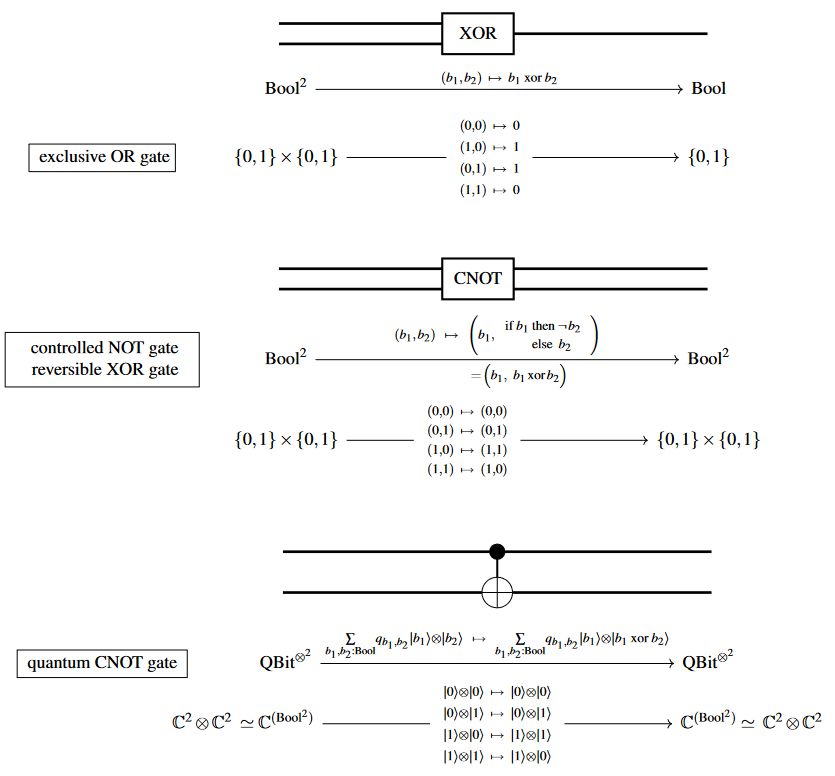
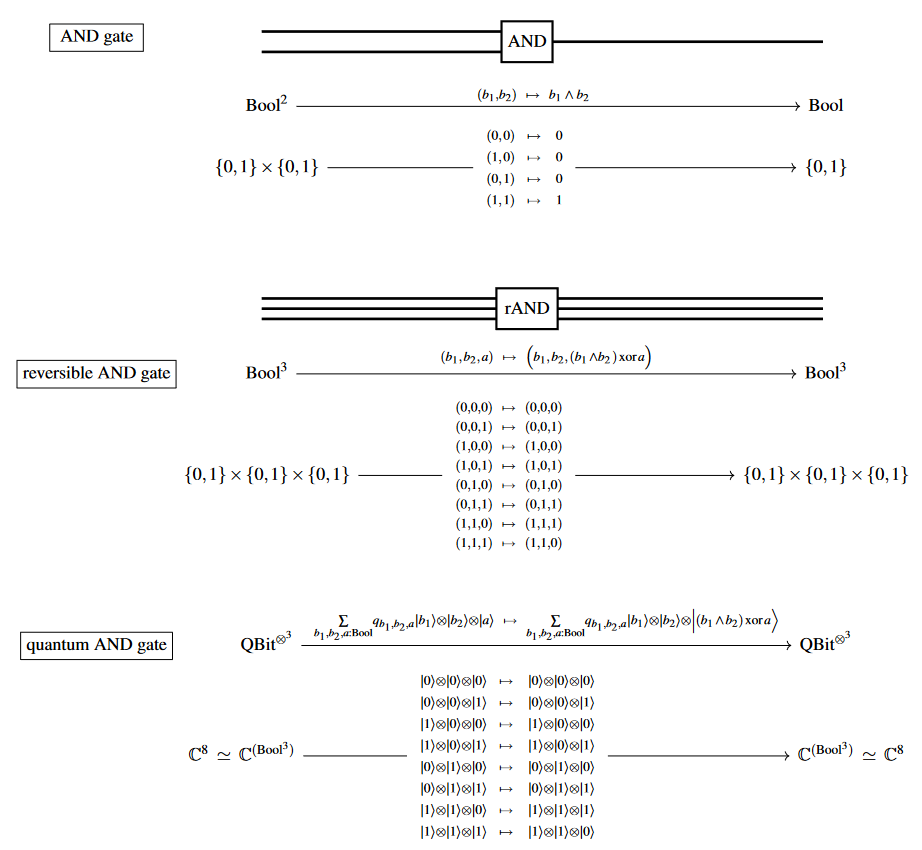
The first examples are linearizations of classical logic gates, or rather of their reversible versions:

NOT or X:

XOR and CNOT:

AND:

The following examples have no classical analog:

Hadamard gate:

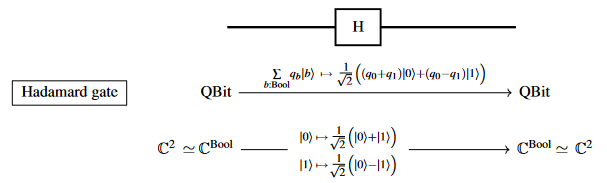
Forther (types of) quantum gates:

• Pauli gates

• Clifford gates

• rotation gates

• T gate, S gate

Related concepts

• logic gate

• controlled quantum gate

• unitary quantum channel

• quantum circuit

• quantum logic

• qbit, qtrit, qdit

References

General

The notion of quantum logic gates and quantum circuits originates with

• Richard Feynman, Quantum mechanical computers, Foundations of Physics 16 (1986) 507–531 [doi:10.1007/BF01886518]

• David E. Deutsch, Quantum computational networks, Proceedings of the Royal Society A, 425 1868 (1989) 73-90 [doi:10.1098/rspa.1989.0099, jstor:2398494]

• Adriano Barenco, Charles H. Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin, Harald Weinfurter, Elementary gates for quantum computation, Phys. Rev. A52 (1995) 3457 [arXiv:quant-ph/9503016, doi:10.1103/PhysRevA.52.3457]

Monograph:

• Michael A. Nielsen, Isaac L. Chuang, §1.3.1-2 in: Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]

On experimental realizations:

• Chen, Church, Englert, Henkel, Rohwedder, Scully, Zubairy: Quantum Computing Devices – Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]

See also:

• Wikipedia, Quantum logic gate

Implementation of quantum logic gates on qbits realized via nucleon-spin, via pulse protocols in nuclear magnetic resonance-technology:

• Price, Somaroo, Tseng, Gore, Fahmy,, Havel, Cory: Construction and Implementation of NMR Quantum Logic Gates for Two Spin Systems, Journal of Magnetic Resonance 140 2 (1999) 371-378 [doi;10.1006/jmre.1999.1851]

and analogously on electron-spin:

• M. Yu. Volkov and K. M. Salikhov, Pulse Protocols for Quantum Computing with Electron Spins as Qubits, Appl Magn Reson 41 (2011) 145–154 [doi:10.1007/s00723-011-0297-2]

Universal gate sets

Review:

• Nielsen & Chuang 2000, §4.5

• Universal set of quantum gates, ICTP-SAIFR presentation (2022) [pdf]

Criteria for universality:

• Adam Sawicki, Katarzyna Karnas: Criteria for universality of quantum gates, Phys. Rev. A 95 062303 (2017) [arXiv:1610.00547, doi:10.1103/PhysRevA.95.062303]

• Adam Sawicki, Lorenzo Mattioli, Zoltán Zimborás: Universality verification for a set of quantum gates (preprint title: How to check universality of quantum gates), Phys. Rev. A 105 (2022) 052602 [doi:10.1103/PhysRevA.105.052602, arXiv:2111.03862]

Proof that CNOT & U(2) is universal:

• Adriano Barenco, Charles H. Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin, Harald Weinfurter: Elementary gates for quantum computation, Phys. Rev. A 52 (1995) 3457 [doi:10.1103/PhysRevA.52.3457, arXiv:quant-ph/9503016]

Proof that CNOT & Hadamard & T gate is universal:

• P. Oscar Boykin, Tal Mor, Matthew Pulver, Vwani Roychowdhury, Farrokh Vatan: On Universal and Fault-Tolerant Quantum Computing: A Novel Basis and a New Constructive Proof of Universality for Shor’s Basis, in 40th Annual Symposium on Foundations of Computer Science (1999) [arXiv:quant-ph/9906054, doi:10.1109/SFFCS.1999.814621]

• P. Oscar Boykin, Tal Mor, Matthew Pulver, Vwani Roychowdhury, Farrokh Vatan: A new universal and fault-tolerant quantum basis, Information Processing Letters 75 3 (2000) 101-107 [doi:10.1016/S0020-0190(00)00084-3, inSpire:2725200]

Proof that CNOT & $R_y(\pi/4)$ & S gate is universal:

• Alexei Kitaev: Quantum computations: algorithms and error correction, Russ. Math. Surv. 52 (1997) 1191 [doi:10.1070/RM1997v052n06ABEH002155]

Proof that Toffoli gate & Hadamard gate is universal (and generally Toffoli & any real single-qbit gate not preserving the measurement basis):

• Yaoyun Shi: Both Toffoli and Controlled-NOT need little help to do universal quantum computation, Quantum Information & Computation 3 1 (2003) 84-92 [doi:10.5555/2011508.2011515, arXiv:quant-ph/0205115]

• Dorit Aharonov: A Simple Proof that Toffoli and Hadamard are Quantum Universal [arXiv:quant-ph/0301040, spire:2727250]

Proof that Hadamard gate & $R_z(\pi/4)$ is universal for single-qbit gates:

• BMPRV99 pp 4

and analogous proof for $R_{x+y}(\pi/2)$ & $R_x(\pi/2)$:

• Google AI quantum et al., VII F.2 (p 30) in: Supplementary information for “Quantum supremacy using a programmable superconducting processor”, Nature, 574 (2019) 505 [arXiv:1910.11333, doi:10.1038/s41586-019-1666-5]