nLab pivotal symbols
The pivotal symbols or symbols are a certain collection of signs attached to a fusion category arising from analyzing how invariant vectors in a -particle state transform under rotation by a full revolution.
In a fusion category, the nature of duals for objects in the category can be encoded in principal -bundle over the simple objects. Firstly, suppose one goes ahead and chooses an arbitrary dual object for every simple object . Write
for the set of ways that can be expressed as a right dual of . Notice that is a -torsor (you can multiply the unit by a nonzero complex number, following which you are forced to multiply the counit by the reciprocal of this number if you want to obey the snake equations).
In a fusion category, if is a right dual of , then it is also a left dual of , though not in a canonical way. This gives us the principal -bundle over the simple objects — the fiber above is
the set of isomorphisms between and .
A pivotal structure or even-handed structure is a section of this bundle satisfying some naturality properties. In other words, it is a consistent way to turn right duals into left duals. The most stringent condition is that the invariant vectors in a tensor product of three particles must either be totally ‘bosonic’ or totally ‘fermionic’ when you rotate them through a full rotation.
That is, the endomorphism
(which can be proved to be an involution) given by sending
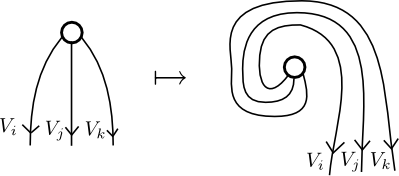
must be equal to . Assuming this is satisfied (if not, there is no consistent way to turn right duals into left duals), we can call this collection of signs the symbols or the pivotal symbols of the fusion category:
That is to say, the symbols are the signs arising from choosing a trivialization of the ‘duality bundle’ and analyzing how invariant -particle tensors transform when they go through a full revolution.
It turns out that one can express the concept of a pivotal structure directly in terms of the pivotal symbols . Namely, a pivotal structure on the category amounts to an -twisted monoidal natural transformation? of the identity on the category. That is to say, a collection of nonzero complex numbers satisfying
whenever appears in . If all the symbols were equal to , this would just be an ordinary monoidal natural transformation of the identity. Perhaps this phenomenon can be understood in a more enlightening way using the language of planar algebras.
References
- P. Etingof, D. Nikshych and V. Ostrik, On fusion categories.
- T. J. Hagge and S-M Hong, Some non-braided fusion categories of rank 3.
- B. Bartlett, On unitary 2-representations of finite groups and topological quantum field theory (chapter 6).
Last revised on July 25, 2020 at 14:17:56. See the history of this page for a list of all contributions to it.