nLab triangle identities
Context
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
2-Category theory
Definitions
Transfors between 2-categories
Morphisms in 2-categories
Structures in 2-categories
Limits in 2-categories
Structures on 2-categories
Contents
Idea
The triangle identities or zigzag identities are identities characterized by the unit and counit of an adjunction, such as a pair of adjoint functors. These identities define, equivalently, the nature of adjunction (this prop.).
Statement
Consider:
-
a pair of categories, or, generally, of objects in a given 2-category;
-
and a pair of functors between these, or generally 1-morphisms in the ambient 2-category;
-
and two natural transformations or, generally 2-morphisms.
This data is called a pair of adjoint functors (generally: an adjunction) if the triangle identities are satisfied, which may be expressed in any of the following equivalent ways:
As equations
As equations, the triangle identities read
Here juxtaposition denotes the whiskering operation of 1-morphisms on 2-morphisms, as made more manifest in the diagrammatic unravelling of these expressions:
As diagrams
In terms of diagrams in the functor categories this means
and
In terms of diagrams of 2-morphisms in the ambient 2-category, this looks as follows:
where on the right the identity 2-morphisms are left notationally implicit.
If we leave the identity 1-morphisms on the left notationally implicit, then we get the following suggestive form of the triangle identities:
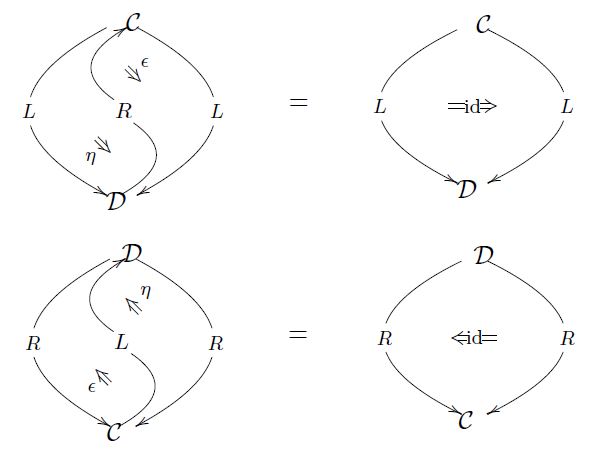
(taken from geometry of physics – categories and toposes).
As string diagrams
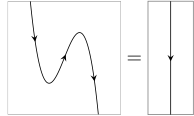
As string diagrams, the triangle identities appear as the action of “pulling zigzags straight” (hence the name):
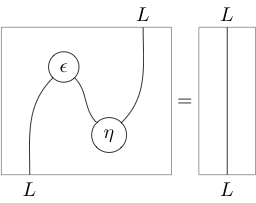
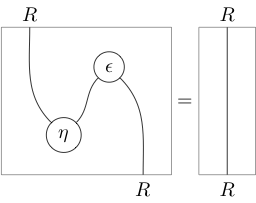
With labels left implicit, this notation becomes very economical:
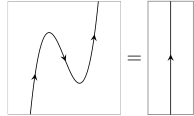
Related concepts
References
Textbook accounts include
- Francis Borceux, Theorem 3.1.5 and Diagram 3.3 in: Basic Category Theory, Vol. 1 of Handbook of Categorical Algebra, Cambridge University Press (1994)
See the references at category theory for more.
Last revised on June 22, 2023 at 16:20:30. See the history of this page for a list of all contributions to it.