nLab Top
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
Definition
Top denotes the category whose objects are topological spaces and whose morphisms are continuous functions between them. Its isomorphisms are the homeomorphisms.
For exposition see Introduction to point-set topology.
Often one considers (sometimes by default) subcategories of nice topological spaces such as compactly generated topological spaces, notably because these are cartesian closed. There other other convenient categories of topological spaces. With any one such choice understood, it is often useful to regard it as “the” category of topological spaces.
The homotopy category of given by its localization at the weak homotopy equivalences is the classical homotopy category Ho(Top). This is the central object of study in homotopy theory, see also at classical model structure on topological spaces. The simplicial localization of Top at the weak homotopy equivalences is the archetypical (∞,1)-category, equivalent to ∞Grpd (see at homotopy hypothesis).
Properties
Universal constructions
We discuss universal constructions in Top, such as limits/colimits, etc. The following definition suggests that universal constructions be seen in the context of as a topological concrete category (see Proposition below).
examples of universal constructions of topological spaces:
Definition
(weak topology and strong topology)
Let be a class of topological spaces, and let be a bare set. Then
-
For a set of functions out of , the initial topology is the topology on with the minimum collection of open subsets such that all are continuous.
-
For a set of functions into , the final topology is the topology on with the maximum collection of open subsets such that all are continuous.
Example
For a single topological space, and a subset of its underlying set, then the initial topology , def. , is the subspace topology, making
a topological subspace inclusion.
Example
Conversely, for an epimorphism, then the final topology on is the quotient topology.
Proposition
Let be a small category and let be an -diagram in Top (a functor from to ), with components denoted , where and a topology on . Then:
-
The limit of exists and is given by the topological space whose underlying set is the limit in Set of the underlying sets in the diagram, and whose topology is the initial topology, def. , for the functions which are the limiting cone components:
Hence
-
The colimit of exists and is the topological space whose underlying set is the colimit in Set of the underlying diagram of sets, and whose topology is the final topology, def. for the component maps of the colimiting cocone
Hence
(e.g. Bourbaki 71, section I.4)
Proof
The required universal property of is immediate: for
any cone over the diagram, then by construction there is a unique function of underlying sets making the required diagrams commute, and so all that is required is that this unique function is always continuous. But this is precisely what the initial topology ensures.
The case of the colimit is formally dual.
Example
The limit over the empty diagram in is the point with its unique topology.
Example
For a set of topological spaces, their coproduct is their disjoint union.
In particular:
Example
For , the -indexed coproduct of the point, , is the set itself equipped with the final topology, hence is the discrete topological space on .
Example
For a set of topological spaces, their product is the Cartesian product of the underlying sets equipped with the product topology, also called the Tychonoff product.
In the case that is a finite set, such as for binary product spaces , then a sub-basis for the product topology is given by the Cartesian products of the open subsets of (a basis for) each factor space.
Example
The equalizer of two continuous functions in is the equalizer of the underlying functions of sets
(hence the largets subset of on which both functions coincide) and equipped with the subspace topology, example .
Example
The coequalizer of two continuous functions in is the coequalizer of the underlying functions of sets
(hence the quotient set by the equivalence relation generated by for all ) and equipped with the quotient topology, example .
Example
For
two continuous functions out of the same domain, then the colimit under this diagram is also called the pushout, denoted
(Here is also called the pushout of , or the cobase change of along .) If is an inclusion, one also write and calls this the attaching space.
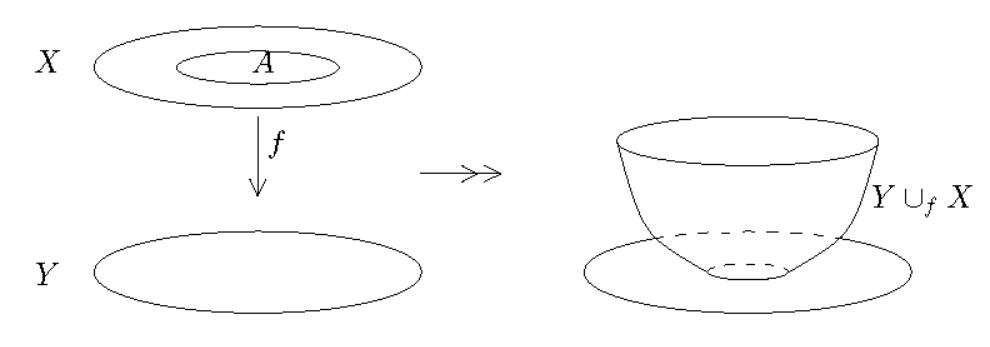
By example the pushout/attaching space is the quotient topological space
of the disjoint union of and subject to the equivalence relation which identifies a point in with a point in if they have the same pre-image in .
(graphics from Aguilar-Gitler-Prieto 02)
Example
As an important special case of example , let
be the canonical inclusion of the standard (n-1)-sphere as the boundary of the standard n-disk (both regarded as topological spaces with their subspace topology as subspaces of the Cartesian space ).
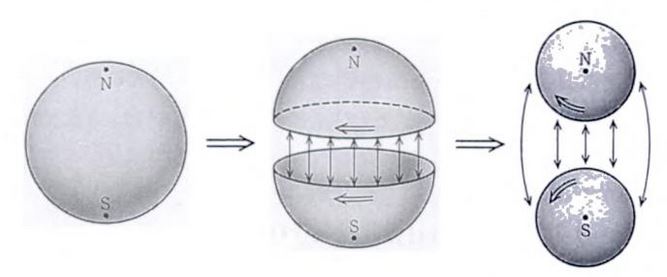
Then the colimit in Top under the diagram, i.e. the pushout of along itself,
is the n-sphere :
(graphics from Ueno-Shiga-Morita 95)
Example
(union of two open or two closed subspaces is pushout)
Let be a topological space and let be subspaces such that
-
are both open subsets or are both closed subsets;
-
they constitute a cover:
Write and for the corresponding inclusion continuous functions.
Then the commuting square
is a pushout square in (example ).
By the universal property of the pushout this means in particular that for any topological space then a function of underlying sets
is a continuous function as soon as its two restrictions
are continuous.
Proof
Clearly the underlying diagram of underlying sets is a pushout in Set. Therefore by prop. we need to show that the topology on is the final topology induced by the set of functions , hence that a subset is an open subset precisely if the pre-images (restrictions)
are open subsets of and , respectively.
Now by definition of the subspace topology, if is open, then the intersections and are open in these subspaces.
Conversely, assume that and are open. We need to show that then is open.
Consider now first the case that are both open open. Then by the nature of the subspace topology, that is open in means that there is an open subset such that . Since the intersection of two open subsets is open, this implies that and hence is open. Similarly . Therefore
is the union of two open subsets and therefore open.
Now consider the case that are both closed subsets.
Again by the nature of the subspace topology, that and are open means that there exist open subsets such that and . Since are closed by assumption, this means that are still closed, hence that are open.
Now observe that (by de Morgan duality)
This exhibits as the intersection of two open subsets, hence as open.
Example
If are normal topological spaces and is a closed embedding of topological spaces and is a continuous function, then in the pushout diagram in (example )
the space is normal and is a closed embedding.
For proof of this and related statements see at colimits of normal spaces.
Relation with
Write Set for the category of sets.
Definition
Write
for the forgetful functor that sends a topological space to its underlying set and which regards a continuous function as a plain function on the underlying sets.
Prop. means in particular that:
Proposition
The category Top has all small limits and colimits. The forgetful functor from def. preserves and lifts limits and colimits.
(But it does not create or reflect them.)
Proposition
The forgetful functor from def. has a left adjoint , given by sending a set to the corresponding discrete topological space, example
Proposition
The forgetful functor from def. exhibits as
Mono-/Epimorphisms
Proposition
(regular monomorphisms of topological spaces)
In the category Top of topological spaces,
-
the monomorphisms are those continuous functions which are injective functions;
-
the regular monomorphisms are the topological embeddings (i.e. those continuous functions which are homeomorphisms onto their images equipped with the subspace topology).
Proof
Regarding the first statement: An injective continuous function clearly has the cancellation property that defines monomorphisms: for parallel continuous functions , if , then , because continuous functions are equal precisely if their underlying functions of sets are equal. Conversely, if has the cancellation property, then testing on points gives that is injective.
Regarding the second statement: from the construction of equalizers in Top (example ) we have that these are topological subspace inclusions.
Conversely, let be a topological subspace embedding. We need to show that this is the equalizer of some pair of parallel morphisms.
To that end, form the cokernel pair by taking the pushout of against itself (in the category of sets, and using the quotient topology on a disjoint union space). By this prop., the equalizer of that pair is the set-theoretic equalizer of that pair of functions endowed with the subspace topology. Since monomorphisms in Set are regular, we get the function back, and again by example , it gets equipped with the subspace topology. This completes the proof.
Intersections and quotients
Lemma
The pushout in Top of any (closed/open) topological subspace inclusion , example , along any continuous function is itself an a (closed/open) subspace .
For proof see there.
Closed monoidal structure
It is well known that Top is not cartesian closed (see for example at convenient category of topological spaces).
It is however closed monoidal.
-
The tensor product is given by the cartesian product of the underlying spaces, equipped with the topology of separate continuity, formed by the sets such that
is an open subset of and
is an open subset of . Equivalently, it is the topology such that for all spaces , a function is continuous if and only if: for every the function is continuous, and for every , the functions is continuous.
-
The internal hom is given by the set of continuous functions , together with the topology of pointwise convergence, generated by the (sub-basic) sets
for each and each open . Equivalently, a net tends to if and only if for all , in .
Related concepts
References
For general references see those listed at topology, such as
- Nicolas Bourbaki, chapter 1 Topological Structures of Elements of Mathematics III: General topology, Springer 1971, 1990
See also
- Marcelo Aguilar, Samuel Gitler, Carlos Prieto, section 12 of Algebraic topology from a homotopical viewpoint, Springer (2002) (toc pdf)
An axiomatic desciption of along the lines of ETCS for Set is discussed in
- Dana Schlomiuk, An elementary theory of the category of topological space, Transactions of the AMS, volume 149 (1970)
For its closed monoidal structure, see:
- Maria Cristina Pedicchio and Fabio Rossi, Monoidal closed structures for topological spaces: counter-example to a question of Booth and Tillotson, Cahiers de topologie et géométrie différentielle catégoriques, 24(4), 1983.
- Appendix A of Paolo Perrone and Ruben Van Belle, Convergence of martingales via enriched dagger categories, 2024. (arXiv)
Last revised on July 26, 2024 at 09:48:17. See the history of this page for a list of all contributions to it.