nLab negation
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Contents
Idea
In (classical) logic, the negation of a statement is a statement which is true if and only if is false. Hence, viewed algebraically, the negation corresponds to the complement operator of the corresponding Boolean algebra which satisfies as well as .
More generally, as different logics correspond to different types of lattices, one calls negation antitone, or polarity reversing, lattice operators that mimic or approximate the algebraic and proof-theoretic behavior of .
As a logic gate
As a logic gate on bits and as a quantum logic gate on qbits (-Pauli matrix):
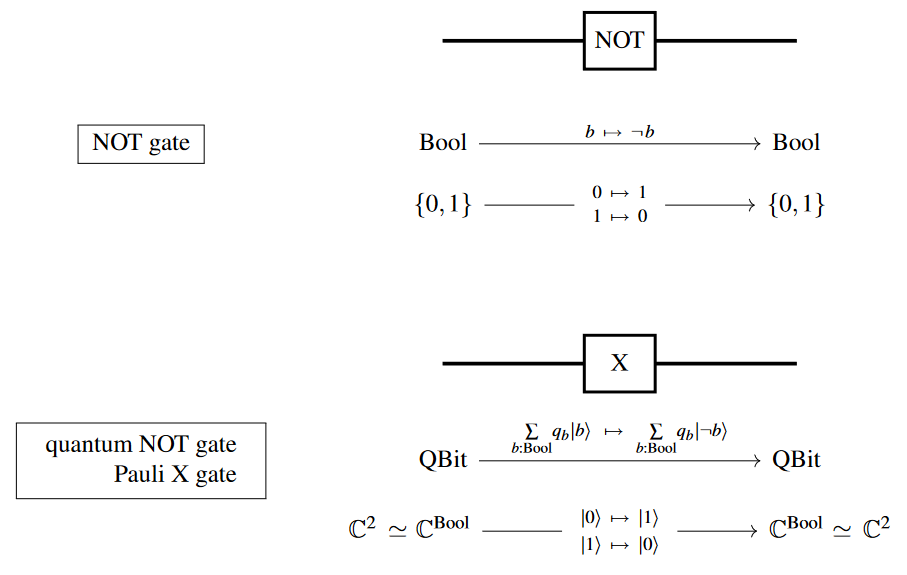
Negation in different logics
In classical logic, we have the double negation law:
In intuitionistic logic, we only have
while in paraconsistent logic, we instead have
One may interpret intuitionistic negation as ‘denial’ and paraconsistent negation as ‘doubt’. So when one says that one doesn't deny , that's weaker than actually asserting ; while when one says that one doesn't doubt , that's stronger than merely asserting . Paraconsistent logic has even been applied to the theory of law: if is a judgment that normally requires only the preponderance of evidence, then is a judgment of beyond reasonable doubt.
Linear logic features (at least) three different forms of negation, one for each of the above. (The default meaning of the term ‘negation’ in linear logic, , is the one that satisfies the classical double-negation law.)
Accordingly, negation mediates de Morgan duality in classical and linear logic but not in intuitionistic or paraconsistent logic.
In type theory syntax
In usual type theory syntax negation is obtained as the function type into the empty type: .
Equivalently, in type theory with equivalence types but without function types, negation is the equivalence type with the empty type: .
In categorical semantics
The categorical semantics of negation is the internal hom into the initial object: .
In a topos, the negation of an object (a proposition under the propositions as types-interpretation) is the internal hom object , where denotes the initial object.
This matches the intuitionistic notion of negation in that there is a natural morphism but not the other way around.
Related entries
References
-
Y. Gauthier, A Theory of Local Negation: The Model and some Applications , Arch. Math. Logik 25 (1985) pp.127-143. (gdz)
-
H. Wansing, Negation , pp.415-436 in Goble (ed.), The Blackwell Guide to Philosophical Logic , Blackwell Oxford 2001.
Last revised on January 4, 2023 at 01:52:39. See the history of this page for a list of all contributions to it.