nLab snake lemma

Idea

A basic lemma in homological algebra: it constructs connecting homomorphisms.

Statement

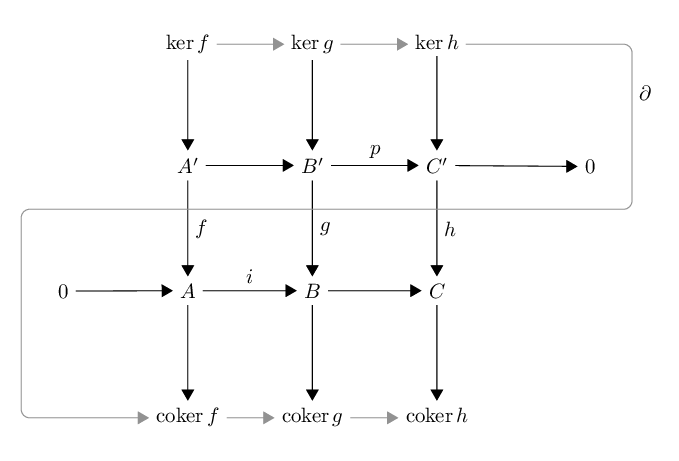
Lemma

Let

$$\array{ && A' &\to & B' &\stackrel{p}{\to}& C' &\to & 0 \\ && \downarrow^{\mathrlap{f}} && \downarrow^{\mathrlap{g}} && \downarrow^{\mathrlap{h}} \\ 0 &\to& A &\stackrel{i}{\to} & B &\to& C }$$

be a commuting diagram in an abelian category $\mathcal{A}$ such that the two rows are exact sequences.

Then there is a long exact sequence of kernels and cokernels of the form

$$ker(f) \to ker(g) \to ker(h) \stackrel{\partial}{\to} coker(f) \to coker(g) \to coker(h) \,.$$

Moreover

• if $A' \to B'$ is a monomorphism then so is $ker(f) \to ker(g)$

• if $B \to C$ is an epimorphism, then so is $coker(g) \to coker(h)$.

If $\mathcal{A}$ is realized as a (full subcategory of) a category of $R$-modules, then the connecting homomorphism $\partial$ here can be defined on elements $c' \in ker(h) \subset C'$ by

$$\partial (c') := i^{-1} \,g\, p^{-1}(c') \,,$$

where $i^{-1}(-)$ and $p^{-1}(-)$ denote any choice of pre-image (the total formula is independent of that choice).

Remark

The snake lemma derives its name from the fact that one may draw the connecting homomorphism $\partial$ that it constructs diagrammatically as follows:

Related concepts

• connecting homomorphism

• salamander lemma

• 3x3 lemma, 5-lemma,

• horseshoe lemma

References

An early occurence of the snake lemma is as lemma (5.8) of

• D. A. Buchsbaum, Exact categories and duality, Transactions of the American Mathematical Society Vol. 80, No. 1 (1955), pp. 1-34 (JSTOR)

In

• Charles Weibel, An introduction to homological algebra

it appears as lemma 1.3.2.

A purely category-theoretic proof is given in

• Temple Fay, Keith Hardie, Peter Hilton, The two-square lemma, Publicacions Matemàtiques, Vol 33 (1989) (pdf)

and in

• Jonathan Wise, A non-elementary proof of the snake lemma (2011, 2023) [pdf, pdf, MO:a/7531]

See also

• Wikipedia, Snake lemma