nLab Dmitri Diakonov

• webpage

Selected writings

• Dmitri Diakonov, Victor Petrov, Exotic baryon resonances in the Skyrme model (arXiv:0812.1212, doi:10.1142/9789814704410_0004), Chapter 3 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)

It is astounding that Skyrme had suggested his model as early as in 1961 before it has been generally accepted that pions are (pseudo) Goldstone bosons associated with the spontaneous breaking of chiral symmetry, and of course long before Quantum Chromodynamics (QCD) has been put forward as the microscopic theory of strong interactions.

The revival of the Skyrme idea in 1983 is due to Witten who explained the raison d’ˆetre of the Skyrme model from the viewpoint of QCD. In the chiral limit when the light quark masses $m_u$, $m_d$, $m_s$ tend to zero, such that the octet of the pseudoscalar mesons π, K , η become nearly massless (pseudo) Goldstone bosons, they are the lightest degrees of freedom of QCD. The effective chiral Lagrangian (EχL) for pseudoscalar mesons, understood as an infinite expansion in the derivatives of the pseudoscalar (or chiral) fields, encodes, in principle, full information about QCD. The famous two-term Skyrme Lagrangian can be understood as a low-energy truncation of this infinite series. Witten has added an important four-derivative Wess–Zumino term to the original Skyrme Lagrangian and pointed out that the overall coefficient in front of the EχL is proportional to the number of quark colours $N_c$.

$[...]$

Soon after Witten’s work it has been realized that it is possible to bring the Skyrme model and the Skyrmion even closer to QCD and to the more customary language of constituent quarks. It has been first noticed $[$6, 7a, 7b, 8$]$ that a simple chiral invariant Lagrangian for massive (constituent) quarks $Q$ interacting with the octet chiral field $\pi_A$ $(A = 1, ..., 8)$,

$$\mathcal{L} = \overline{Q} \left( \mathrlap{\partial}/ - M e^{ \tfrac{i \pi^A \lambda^A \gamma_5}{F_\pi} } \right) Q$$

induces, via a quark loop in the external pseudoscalar fields (see Fig. 3.1), the EχL whose lowest-derivative terms coincide with the Skyrme Lagrangian, including automatically the Wess–Zumino term, with the correct coefficient!

$[...]$

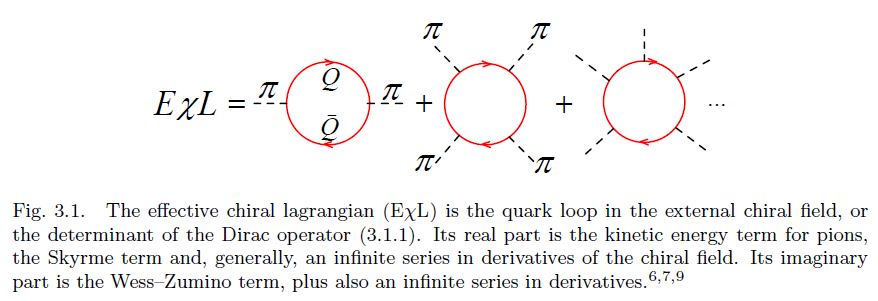
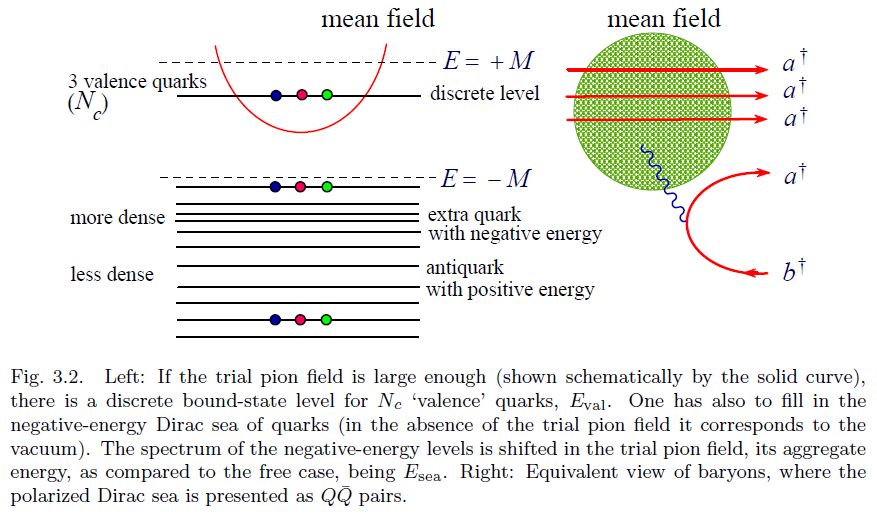
The condition that the winding number of the trial field is unity needs to be imposed to get a deeply bound state, that is to guarantee that the baryon number is unity. $[$9$]$ The Skyrmion is, thus, nothing but the mean chiral field binding quarks in a baryon.

• Dmitri Diakonov, Michael I. Eides, Chiral Lagrangian from a functional integral over quarks, JETP Letters 38.7 (1983): 433-436 (pdf, pdf)

• A. Dhar, Spenta R. Wadia, Nambu—Jona-Lasinio Model: An Effective Lagrangian for Quantum Chromodynamics at Intermediate Length Scales, Phys. Rev. Lett. 52, 959 (1984) (doi:10.1103/PhysRevLett.52.959)

• Avinash Dhar, R. Shankar, Spenta R. Wadia, Nambu–Jona-Lasinio–type effective Lagrangian: Anomalies and nonlinear Lagrangian of low-energy, large-N QCD, Phys. Rev. D 31, 3256 (1985) (doi:10.1103/PhysRevD.31.3256)

• Dmitri Diakonov, Victor Petrov, A theory of light quarks in the instanton vacuum, Nuclear Physics B Volume 272, Issue 2, 21 July 1986, Pages 457-489 (doi:10.1016/0550-3213(86)90011-8)

• Dmitri Diakonov, Victor Petrov, P.V. Pobylitsa, A Chiral Theory of Nucleons, Nucl. Phys. B306 (1988) 809 (spire:247700, doi:10.1016/0550-3213(88)90443-9)

category: people