nLab Hermann Grassmann

Hermann Grassmann was a German polymath, 1809-1877. Among many other accomplishments, an early inventor of linear algebra and notably of Grassmann algebra (exterior algebra, hence superalgebra), which he laid out in his book Ausdehnungslehre.

• Wikipedia entry

The appreciation of Grassmann’s ideas took a long time:

From Drew Armstrong:

Perhaps owing to the abstraction of his work, he was not recognized by the mathematical community and was more famous during his lifetime for his work in philology (including a translation of the Rig Veda). Despite his failure to achieve mathematical success, Grassmann never doubted that his work was significant. Here’s a striking quote from the preface of the 1862 second edition of the Ausdehnungslehre:

I remain completely confident that the labour I have expended on the science presented here and which has demanded a significant part of my life as well as the most strenuous application of my powers, will not be lost. It is true that I am aware that the form which I have given the science is imperfect and must be imperfect. But I know and feel obliged to state (though I run the risk of seeming arrogant) that even if this work should again remain unused for another seventeen years or even longer, without entering into the actual development of science, still that time will come when it will be brought forth from the dust of oblivion and when ideas now dormant will bring forth fruit. I know that if I also fail to gather around me (as I have until now desired in vain) a circle of scholars, whom I could fructify with these ideas, and whom I could stimulate to develop and enrich them further, yet there will come a time when these ideas, perhaps in a new form, will arise anew and will enter into a living communication with contemporary developments. For truth is eternal and divine.

(Translation from Michael Crowe, A History of Vector Analysis)

Here is R. W. Genese in 1893 (Nature volume 48, page 517) lamenting the delay in its translation:

Sir Robert Ball asks why no one has translated the “Ausdehnungslehre” into English. The answer is as regretable as simple—it would not pay. The number of mathematicians who, after the severe courses of the universities, desire to extend their reading is very small. It is something that a respectable few seek to apply what they have already learnt. The first duty of those who direct the studies of the universities is to provide that students may leave in possession of all the best means of future investigation. That fifty years after publication the principles of the “Ausdehnungslehre” should find no place in English mathematical education is indeed astonishing. Half the time given to such a wearisome subject as Lunar Theory would place a student in possession of many of the delightful surprises of Grassmann’s work, and set him thinking for himself. The “Ausdehnungslehre” has won the admiration of too many distinguished mathematicians to remain longer ignored. Clifford said of it: “I may, perhaps, be permitted to express my profound admiration of that extraordinary work, and my conviction that its principles will exercise a vast influence upon the future of mathematical science.” Useful or not, the work is “a thing of beauty,” and no mathematician of taste should pass it by. It is possible, nay, even likely, that its principles may be taught more simply; but the work should be preserved as a classic.

Grassmann’s ideas were finally studied in

• Hermann Hankel, Vorlesungen über die Complexen Zahlen und ihre Functionen, Leipzig: Leopold Voss, 1867.

His ideas were developed by William Kingdon Clifford who turned Grassmann algebras into Clifford algebras in

• William Clifford, Applications of Grassmann’s extensive algebra, American Journal of Mathematics 1 (4): 350–358. (1878). doi:10.2307/2369379.

Today Grassmann algebra is ubiquituous in differential geometry (de Rham algebra, supergeometry) and superalgebra. In fact, Grassmann had invented the sign rule of supercommutative superalgebra, which was fully appreciated only in the second half of the 20th century:

from Grassmann 1844, p. 61 and 84

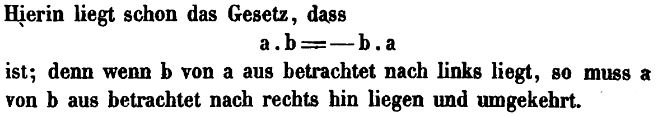
This way Grassmann’s prediction on the eventual impact of his work did become true. From Freeman Dyson, Missed opportunities (doi:10.1090/S0002-9904-1972-12971-9):

In the year 1844 two remarkable events occurred, the publication by Hamilton of his discovery of quaternions, and the publication by Grassmann of his “Ausdehnungslehre.” With the advantage of hindsight we can see that Grassmann’s was the greater contribution to mathematics, containing the germ of many of the concepts of modern algebra, and including vector analysis as a special case. However, Grassmann was an obscure high-school teacher in Stettin, while Hamilton was the world-famous mathematician whose official titles occupy six lines of print after his name at the beginning of his 1844 paper. So it is regrettable, but not surprising, that quaternions were hailed as a great discovery, while Grassmann had to wait 23 years before his work received any recognition at all from professional mathematicians. When Grassmann’s work finally became known, mathematicians were divided into quaternionists and antiquaternionists, and were spending more energy in polemical arguments for and against quaternions than in trying to understand how Grassmann and Hamilton might be fitted together into a larger scheme of things.

Grassmann also had a profound influence on the thought of Gottlob Frege. See Sec. 2.1.1 of

• Paolo Mancosu, Abstraction and infinity, Oxford University Press, 2017.

Writings

• Hermann Grassmann, Die Lineale Ausdehnungslehre ein neuer Zweig der Mathematik, dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auchauf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert, Leipzig: Otto Wiegand, 1844. English translation in Grassmann 1915.

This was revised in a second edition published 18 years later:

• Hermann Grassmann, Die Ausdehnungslehre: Vollständig und in strenger Form bearbeitet, Berlin: Enslin, 1862. English translation, 2000, by Lloyd Kannenberg, Extension Theory, American Mathematical Society.

Other writings include

• Hermann Grassmann, Geometrische Analyse geknüpft an die von Leibniz erfundenegeometrische Charakteristik. Gekrönte Preisschrift, Leipzig: Wiedmann, 1847. English translation in Grassmann 1915.

• Hermann Grassmann, Lehrbuch der Arithmetik für höhere Lehranstalten, Berlin: Enslin, 1861. (Google Books)

• Hermann Grassmann, A New Branch of Mathematics. The Ausdehnungslehre of 1844 and Other Works, edited and translated by L. C. Kannenberg, Chicago: Open Court, 1915.

category: people