nLab signs in supergeometry
Context
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
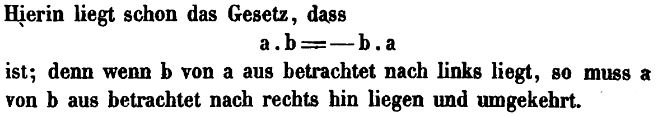

Contents
- Idea
- The sign rule from internalization
- Differential forms on supermanifolds
- Cohomology of super Minkowski spacetime
- Super Lie algebra cohomology
- Presheaves on superpoints
- The super odd sign rule
- Relation between the two sign rules
- Strong symmetric monoidal equivalence
- Equivalence of super Lie algebra cohomology in both conventions
- References
Idea
Discussion of superalgebra and supergeometry involves, by definition, crucial minus signs appearing in certain expressions. While there is a systematic rule for these, when superalgebra/supergeometry is combined with other topics that crucially involve their own signs, such as homological algebra, or ordering of terms, such as in noncommutative algebra, then the combined sign rule may appear intricate. This page here is meant to explicitly list two equivalent sign rules for easy reference. We follow (Deligne-Freed 99) which has the same goal.
The main point to notice is that for algebraic terms that have both a homological degree and a super-degree the “internalization sign rule” for the sign when exchanging two such elements is
(e.g. Castellani-D’Auria-Fré 91, (II.2.109), Bonora-Bregola-Lechner-Pasti-Tonin 87, beginning of section 2)
This we discuss below at The sign rule from internalization.
Parts of the literature however adops another sign rule, given by
This we discuss below in The super odd sign rule.
In Deligne-Morgan 99, the two sign rules are referred to as Deligne’s convention (for the internalization rule) and Bernstein’s convention (for the super odd sign rule).
sign rule for differential graded-commutative superalgebras
(different but equivalent)
| Deligne’s convention | Bernstein’s convention | |
|---|---|---|
| common in discussion of | supergravity | AKSZ sigma-models |
| representative references | Bonora et. al 87, Castellani-D’Auria-Fré 91, Deligne-Freed 99 | AKSZ 95, Carchedi-Roytenberg 12 |
The sign rule from internalization
Here and in the following we adopt the perpective that homological algebra in superalgebra is concerned with the study of chain complexes internal to the symmetric monoidal category of super vector spaces (Deligne 90) or equivalently internal to the topos over superpoints (Schwarz 84). This means that there are two contributions to the sign when exchanging two terms, one from the cohomological grading, one from the super-grading. This is “the sign rule” also used for instance in (Castellani-D’Auria-Fré 91, equation (II.2.106), Bonora-Bregola-Lechner-Pasti-Tonin 87 Deligne-Freed 99, section 6).
There is however also a different sign rule use in the literature, the relation to which we discuss below.
Differential forms on supermanifolds
We discuss the sign rules for the de Rham algebra of differential forms on a supermanifold (superdifferential forms), which is a differential graded-commutative superalgebra.
For , let the super Cartesian space of dimension . This is the supermanifold defined by the fact that its algebra of functions is freely generated, as a smooth superalgebra by even-graded coordinate-functions and odd-graded coordinate function
Accordingly, by the discussion at Kähler forms, the de Rham complex of differential forms on is freely generated as a super-module over the smooth superalgebra by expressions of the form .
This de Rham complex now carries the structure of a
- differential graded-commutative graded commutative superalgebra
which should be thought of as bracketet as follows
- differential graded-commutative graded (commutative superalgebra).
This means in effect that elements of carry a -grading, where we may say that
-
corresponds to the “cohomological grading”;
-
corresponds to the super-grading.
We write
for elements in this grading group.
In this notation the grading of the elements in is all induced by the fact that the de Rham differential itself is a derivation of degree .
| generator | bi-degree |
|---|---|
| (0,even) | |
| (0,odd) | |
| (1,even) |
Here the last line means that we have
| generator | bi-degree |
|---|---|
| (0,even) | |
| (0,odd) | |
| (1,even) | |
| (1,odd) |
The formula for the “cohomologically- and super-graded commutativity” in is
for all of homogeneous -degree. Hence there are two contributions to the sign picked up when exchanging two super-differential forms in the wedge product:
-
there is a “cohomological sign” which for commuting an -forms past an -form is ;
-
in addition there is a “super-grading” sich which for commuting a -graded coordinate function past a -graded coordinate function (possibly under the de Rham differential) is .
Some examples:
| sign rule | Deligne’s | Bernstein’s |
|---|---|---|
Cohomology of super Minkowski spacetime
The above signs rules for differential forms on supermanifolds directly translate to the signs rule for super Lie algebra Lie algebra cohomology, by the identification of elements in the Chevalley-Eilenberg algebra with the left invariant differential forms on the corresponding super Lie group.
We discuss now the Chevalley-Eilenberg algebra of super Minkowski spacetime, regarded as a super translation Lie algebra, equivalently as the quotient of the quotient of the super Poincaré Lie algebra by the Lorentz Lie algebra.
This is the sub-algebra of the above de Rham complex of the left invariant differential forms:
With the above notation these are
With the above sign rules it follows that
Super Lie algebra cohomology
More generally, since the super-Chevalley-Eilenberg algebra of a super Lie algebra is identified with the left invariant differential forms on the corresponding super Lie group, the signs from the super de Rham complex above induce the cotresponding sign rule for the computation of super-Lie algebra cohomology.
Presheaves on superpoints
Write for the category of superpoints, the opposite category of that of real finitely-generated Grassmann algebras.
We list the terms with crucial signs that appear when regarding superalgebra as algebra internal to the presheaf topos over superpoints (see at super infinity-groupoid for background).
Super Lie algebras
Given a super Lie algebra , for each superpoint write
for the vector space which is the even-degree part of the tensor product of the underlying vector spaces of and of the Grassmann algebra .
Here if is a basis for with a basis for and a basis for , and if we write for the generators of , then is generated from elements of the form
and
The Lie bracket on the ordinary vector space is defined on elements
by the formula
Some examples:
From this and from the ordinary skew-symmetry of the Lie bracket in follows that also in the super Lie algebra we have
Next, from
and the fact that it follows that in the super Lie algebra
Chevalley-Eilenberg algebra
Given a super Lie algebra as above, the tensor product is the free -module generated from the super vector space underlying .
(…)
(…)
(…)
The super odd sign rule
In all of the above we used the sign rule induced by setting up all mathematical concepts internal to the symmetric monoidal category of super vector spaces or internal the topos over superpoints.
There is another sign convention in the literature, for instance in (…). In this convention one considers the map
to induce a single -grading and then lets all signs be induced by that.
This can motivated from regarding the -graded de Rham complex of a supermanifold as the algebra of functions on its odd-shifted tangent bundle
In this convention a term such as of bidegree has single degree and hence commutes with every other term.
Differential forms on a supermanifold in the super odd convention
In this other convention the signs in the de Rham complex of the super Cartesian space are induced as follows:
Relation between the two sign rules
Strong symmetric monoidal equivalence
The two sign rules correspond to two different symmetric braiding-structures on the monoidal category of chain complexes of super vector spaces. The corresponding two kinds of differential graded-commutative superalgebras are the commutative monoid objects with respect to these two choices.
We now show that the two braidings are equivalent (Prop. below), which immediately implies that the two categories of differential graded-commutative algebras are equivalent.
Definition
(chain complexes of super vector spaces)
Write for the category of chain complexes inside the category of super vector spaces.
Hence for an object, for each there is a super vector space
where we write the elements of the group of order two as , with being the neutral element.
Hence we may regard any equivalently as a -graded vector space equipped with a differential of degree . For an element in definite (“homogeneous”) bi-degree, we denote this degree by
The category becomes a monoidal category under the tensor product of chain complexes applied to the tensor product of super vector spaces. This means that for , the differential on a homogeneously graded element is
Proposition
(symmetric monoidal structure on category of chain complexes of super vector spaces)
The monoidal category of chain complexes of super vector spaces from Def. becomes a symmetric monoidal with each of the following two braiding isomorphisms, defined on tensor products of elements in homogenous bi-degree (1) as follows:
-
;
-
.
Here in the exponents we are using the canonical ring-structure on the integers and on the prime field , the implicit ring homomorphism and we understand that and .
Proof
Since the expressions for both sign factors are symmetric in and in both cases, it is clear that in both cases. Hence if is indeed a braiding, then it is symmetric.
To see that is indeed a braiding in each case, we need to check the hexagon identities
and
Since differs only by multiplication by a sign from the standard symmetric braiding on the category of vector spaces, which does satisfy its hexagon identities, it just remains to check that these sign factors picked up in going both ways around these diagrams agree.
Hence for the two hexagon identities are equivalent to the conditions
and
while for they are equivalent to the conditions
and
for all triples of bi-degrees .
In both cases this holds because already the relevant exponents are equal in each case, by the distributive law for multiplication and addition in .
Proposition
(the two symmetric monoidal structures on the category of chain complexes of super vector spaces are equivalent)
The two symmetric monoidal category structures and on the monoidal category of chain complexes of super vector spaces from Prop. are equivalent
in that the identity functor equipped with the following monoidal natural isomorphism
(the second line shows its action on elements of homogeneous bidegree )
becomes a strong symmetric monoidal functor
Proof
First to see that we have a strong monoidal functor, we need to check the associativity condition
and the unitality conditions
and
Since differs from the trivial monoidal isomorphism only by the sign factor, this is equivalent to the condition that the sign factors picked up in going both ways around these diagrams agree.
For associativity this is the condition
for all bi-degrees , which holds, because it already holds for the exponents themselves, as an identity in .
For the unitality condition this is the statement that the sign given by and is the the trivial sign . This is indeed the case because the tensor unit is in degree .
Now to see that we have a symmetric monoidal functor, we need to show that it intertwines the two symmetruc braiding isomorphisms
As before, this is equivalent to a condition on the signs picked up both ways, which reads:
Inspection shows that this is indeed the case:
The two signs of and differ by the “mixed terms” that are produced in multiplying out and these two mixed terms is just what the two occurences provides (using that ).
Equivalence of super Lie algebra cohomology in both conventions
The different choice of signs in the de Rham complex above affects the signs of any super-Chevalley-Eilenberg algebra, by the identification of elements in the CE-algebra with left invariant differential forms on the supegroup.
We show now that as chain complexes the two CE-algebras are quasi-isomorphic and hence do have the same cochain cohomology, hence that the definition of super-Lie algebra cohomology is not affected by the different perspective on signs.
(This follows abstract from Prop. , but we spell it out concretely.)
A chain-isomorphism can be obtained as follows:
Write
-
for the cochain complex underlying the Chevalley-Eilenberg algebra with the signs given by
-
write for the cochain complex obtained with the sign rule
Say that a product of generators representing an element in is in normal order of all the -graded elements are left of the -graded elements, schematically
To define a linear map declare that elements in this normal form go to the elements given by the same expression.
This defines a linear map in each degree . Notice that this is not a morphism of algebras, in any sense, but it is a chain map. To see this, notice that acting with the differential which is of degree on a term of the form produces a sum of such terms where in each summand one generator is replaced by a term of the form or by , respectively. These are in turn themselves sums of elements of the form . By commuting them to the middle we see that the differential of the whole term is a sum of terms of the form
and
Now observe:
-
for terms of the first type, the signs picked up by commuting to the middle are by definition the same in and in ;
-
for terms of the second type there are a priori more signs picked up in than in , namely one for every term that one commutes through. But as the differential first passes from the left into the string of s and then in turn is passed back to the left, these extra signs appear in even number and hence cancel out.
In summary this establishes a chain map which is an cochain isomorphism and hence in particular a quasi-isomorphism, hence an isomorphism on cochain cohomology.
References
Internalization sign rule
The internalization into the topos over superpoints is due to
- Albert Schwarz, On the definition of superspace, Teoret. Mat. Fiz. (1984) Volume 60, Number 1, Pages 37–42, (russian original pdf)
The internalization sign rule follows for instance from applying the construction of internal Grassmann algebras in the category of super vector space as discussed in
- Pierre Deligne, p. 165 in: Catégories Tannakiennes, Grothendieck Festschrift, vol. II, Birkhäuser Progress in Math. 87 (1990) 111-195.
The corresponding internal sign rule appears for instance in
-
Loriano Bonora, M. Bregola, Kurt Lechner, Paolo Pasti, Mario Tonin, section 2 of: Anomaly-free supergravity and super-Yang-Mills theories in ten dimensions, Nuclear Physics B 296 4 (1988) [doi:10.1016/0550-3213(88)90402-6]
-
Leonardo Castellani, Riccardo D'Auria, Pietro Fré, equations (II.2.106) and (II.2.109) in: Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991) [doi:10.1142/0224, toc: pdf, chII.2: pdf]
-
Pierre Deligne, Dan Freed, Sign manifesto, (1999) [pdf, pdf]
which appears in
- Pierre Deligne, Daniel Freed, Supersolutions [arXiv:hep-th/9901094]
which in turn appears in
- P. Deligne, P. Etingof, D.S. Freed, L. Jeffrey, D. Kazhdan, John Morgan, David Morrison, E. Witten (eds.) Quantum Fields and Strings, A course for mathematicians, 2 vols. Amer. Math. Soc. Providence (1999) 357-366 [ISBN:978-0-8218-2014-8, web version]
And with explicit acknowledgement that there is also the alternative super odd sign rule in:
-
Pierre Deligne, John Morgan, Notes on supersymmetry (following Joseph Bernstein) [pdf]
pp. 62 (pdf)
in: P. Deligne, P. Etingof, D.S. Freed, L. Jeffrey, D. Kazhdan, John Morgan, David Morrison, E. Witten (eds.) Quantum Fields and Strings, A course for mathematicians, 2 vols. Amer. Math. Soc. Providence (1999) 41-97 [ISBN:978-0-8218-2014-8 web version]
-
Ivan Mirković, remark 1.2.8 in: Notes on Super Math, in Quantum Field Theory Seminar, lecture notes (2004) [pdf, pdf]
See also:
- Daniel Freed, bottom of p. 48 in Classical field theory and Supersymmetry, IAS/Park City Mathematics Series Volume 11, 2001 (pdf)
Super odd sign rule
- David Carchedi, Dmitry Roytenberg, Homological Algebra for Superalgebras of Differentiable Functions (arXiv:1212.3745)
…
Last revised on March 9, 2024 at 03:10:41. See the history of this page for a list of all contributions to it.