nLab Ausdehnungslehre

This page collects material related to the book

• Hermann Grassmann,

  Die Wissenschaft der extensiven Grössen oder die Ausdehnungslehre

  Erster Teil, die lineale Ausdehnungslehre,

  1844

  (pdf scan of original, Internet Archive copy)

which introduced for the first time basic concepts of what today is known as linear algebra (including affine spaces as torsors over vector spaces) and introduced in addition an exterior product (§37, §55) on vectors, forming what today is known as exterior algebra or Grassmann algebra, hence in fact superalgebra (see below).

Grassmann advertizes his work (p. xxv) as being the theory of extensive quantity. The modern way of speaking about this is that the elements of the exterior algebra he considered are differential forms on Euclidean space.

Prominent followups are:

• Giuseppe Peano, Calcolo Geometrico secondo l’Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva, Fratelli Bocca Editori, Torino, 1888, pp. XI, 171 [Mathematica Italiana opere 138, pdf]

which introduces the modern concept of vector spaces.

and

• William Clifford, Applications of Grassmann’s extensive algebra, American Journal of Mathematics 1 4 (1878) 350-358 [doi:10.2307/2369379, jstor:2369379]

which introduces the notion of Clifford algebra.

Content

Supercommutative superalgebra

Here is Grassmann introducing the sign rule of supercommutative superalgebra:

from Grassmann 1844, p. 61

from Grassmann 1844, p. 84

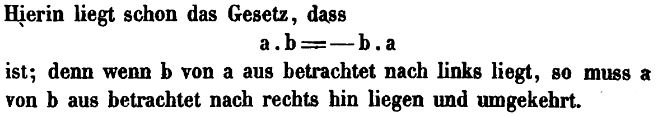
Reception

The appreciation of Grassmann’s ideas took a long time:

From Drew Armstrong:

Perhaps owing to the abstraction of his work, he was not recognized by the mathematical community and was more famous during his lifetime for his work in philology (including a translation of the Rig Veda). Despite his failure to achieve mathematical success, Grassmann never doubted that his work was significant. Here’s a striking quote from the preface of the 1862 second edition of the Ausdehnungslehre:

I remain completely confident that the labour I have expended on the science presented here and which has demanded a significant part of my life as well as the most strenuous application of my powers, will not be lost. It is true that I am aware that the form which I have given the science is imperfect and must be imperfect. But I know and feel obliged to state (though I run the risk of seeming arrogant) that even if this work should again remain unused for another seventeen years or even longer, without entering into the actual development of science, still that time will come when it will be brought forth from the dust of oblivion and when ideas now dormant will bring forth fruit. I know that if I also fail to gather around me (as I have until now desired in vain) a circle of scholars, whom I could fructify with these ideas, and whom I could stimulate to develop and enrich them further, yet there will come a time when these ideas, perhaps in a new form, will arise anew and will enter into a living communication with contemporary developments. For truth is eternal and divine.

(Translation from Michael Crowe, A History of Vector Analysis)

Here is R. W. Genese in 1893 (Nature volume 48, page 517) lamenting the delay in its translation:

Sir Robert Ball asks why no one has translated the “Ausdehnungslehre” into English. The answer is as regretable as simple—it would not pay. The number of mathematicians who, after the severe courses of the universities, desire to extend their reading is very small. It is something that a respectable few seek to apply what they have already learnt. The first duty of those who direct the studies of the universities is to provide that students may leave in possession of all the best means of future investigation. That fifty years after publication the principles of the “Ausdehnungslehre” should find no place in English mathematical education is indeed astonishing. Half the time given to such a wearisome subject as Lunar Theory would place a student in possession of many of the delightful surprises of Grassmann’s work, and set him thinking for himself. The “Ausdehnungslehre” has won the admiration of too many distinguished mathematicians to remain longer ignored. Clifford said of it: “I may, perhaps, be permitted to express my profound admiration of that extraordinary work, and my conviction that its principles will exercise a vast influence upon the future of mathematical science.” Useful or not, the work is “a thing of beauty,” and no mathematician of taste should pass it by. It is possible, nay, even likely, that its principles may be taught more simply; but the work should be preserved as a classic.

Grassmann’s ideas were finally studied in

• Hermann Hankel, Vorlesungen über die Complexen Zahlen und ihre Functionen, Leipzig: Leopold Voss, 1867.

His ideas were developed by William Kingdon Clifford who turned Grassmann algebras into Clifford algebras in

• William Clifford, Applications of Grassmann’s extensive algebra, American Journal of Mathematics 1 (4): 350–358. (1878). doi:10.2307/2369379.

Today Grassmann algebra is ubiquituous in differential geometry (de Rham algebra, supergeometry) and superalgebra. In fact, Grassmann had invented the sign rule of supercommutative superalgebra, which was fully appreciated only in the second half of the 20th century.

This way Grassmann’s prediction on the eventual impact of his work did become true. From Freeman Dyson, Missed opportunities (doi:10.1090/S0002-9904-1972-12971-9):

In the year 1844 two remarkable events occurred, the publication by Hamilton of his discovery of quaternions, and the publication by Grassmann of his “Ausdehnungslehre.” With the advantage of hindsight we can see that Grassmann’s was the greater contribution to mathematics, containing the germ of many of the concepts of modern algebra, and including vector analysis as a special case. However, Grassmann was an obscure high-school teacher in Stettin, while Hamilton was the world-famous mathematician whose official titles occupy six lines of print after his name at the beginning of his 1844 paper. So it is regrettable, but not surprising, that quaternions were hailed as a great discovery, while Grassmann had to wait 23 years before his work received any recognition at all from professional mathematicians. When Grassmann’s work finally became known, mathematicians were divided into quaternionists and antiquaternionists, and were spending more energy in polemical arguments for and against quaternions than in trying to understand how Grassmann and Hamilton might be fitted together into a larger scheme of things.

Grassmann also had a profound influence on the thought of Gottlob Frege. See Sec. 2.1.1 of

• Paolo Mancosu, Abstraction and infinity, Oxford University Press, 2017.

Discussion

Discussion of the book includes

• William Lawvere, Grassmann’s Dialectics and Category Theory, in Hermann Günther Graßmann (1809–1877): Visionary Mathematician, Scientist and Neohumanist Scholar, Boston Studies in the Philosophy of Science Volume 187, 1996, pp 255-264, doi:10.1007/978-94-015-8753-2_21

and the similar text

• William Lawvere, A new branch of mathematics, “The Ausdehnungslehre of 1844,” and other works. Open Court (1995), Translated by Lloyd C. Kannenberg, with foreword by Albert C. Lewis, Historia Mathematica Volume 32, Issue 1, February 2005, Pages 99–106, doi:10.1016/j.hm.2004.07.004

which says at one point that full appreciation of the Ausdehnungslehre requires concepts of category theory

The modern conceptual apparatus, involving levels of structure, categories of morphisms preserving given structure, forgetful reduct functors between categories, the adjoints to such functors, etc., seems to be necessary for ordinary mortals to be able to find their way through the riches of Grassmann’s geometry.

The first part of the introduction of the Ausdehnungslehre is concerned with philosophy, about which

Grassmann insists that his reason for including it is an attempt to provide an orientation to help the student form for himself the proper estimation of the relation between general and particular at every stage of the learning process (Lawvere 95).

The second part of the introduction, titled Survey of the general theory of forms considers key concepts of algebra. For instance it considers the associativity law and states its coherence law (§3).

Grassmann writes that he uses the term “form” in place of “quantity” (German: “Grösse”) (Introduction A.3, §2). It is “forms” that his algebraic operations are defined on, and which are produced by these.

The last half of that introduction is essentially one of the first expositions of the rudimentary principles of what today might be called universal algebra. The content of the first half, after considerable study of the compact formulations, appears to be a simple and clear natural scientist’s version of the basic principles of dialectical materialism, as applied to the formal sciences. (Lawvere 95)

Curiously, while Grassmann complains (on p. xv) about the “unclarity and arbitrariness” of Hegel‘s school of philosophy (German idealism, predominant in Germany at Grassmann’s time), the introduction of the Ausdehnungslehre has much the same sound as Hegel, notably it discusses “categories” such as being, becoming (p. xxii), particulars (p.xx) and the dialectic of opposites such as discrete $\dashv$ continuous (p.xxii) and, notably, of intensive and extensive quantity (p. xxiv-xxv), which Grassmann advertizes as the very topic of his mathematical theory. That of course is the difference to Hegel, that unambiguous mathematical formalization of these otherwise vague concepts is provided (according to Lawvere 95 Grassmannn’s formalization of the pair being and becoming is via points and vectors in an affine space), and in this sense Grassmann is clearly a forerunner of Lawvere’s various proposals for formalizing Hegel’s objective logic in categorical logic/topos theory (as discussed at Science of Logic).

Related entries

• Grassmann algebra

• supercommutative superalgebra

• Berezin integral, integration over supermanifolds

References

• Wikipedia, Grassmann – Mathematician

• Freeman Dyson, Missed opportunities, Bulletin of the AMS, Volume 78, Number 5 (1972) pp 635-652, doi:10.1090/S0002-9904-1972-12971-9

  In the year 1844 two remarkable events occurred, the publication by Hamilton of his discovery of quaternions, and the publication by Grassmann of his “Ausdehnungslehre.” With the advantage of hindsight we can see that Grassmann’s was the greater contribution to mathematics, containing the germ of many of the concepts of modern algebra, and including vector analysis as a special case. However, Grassmann was an obscure high-school teacher in Stettin, while Hamilton was the world-famous mathematician whose official titles occupy six lines of print after his name at the beginning of his 1844 paper. So it is regrettable, but not surprising, that quaternions were hailed as a great discovery, while Grassmann had to wait 23 years before his work received any recognition at all from professional mathematicians. When Grassmann’s work finally became known, mathematicians were divided into quaternionists and antiquaternionists, and were spending more energy in polemical arguments for and against quaternions than in trying to understand how Grassmann and Hamilton might be fitted together into a larger scheme of things.

category: reference