nLab Yoneda embedding

Idea

For $C$ a locally small category, every object $X$ of $C$ induces a presheaf on $C$: the representable presheaf $h_X$ represented by $X$. This assignment extends to a functor $C \to [C^{op}, Set]$ from $C$ to its category of presheaves. The Yoneda lemma implies that this functor is full and faithful and hence realizes $C$ as a full subcategory inside its category of presheaves.

Recall from the discussion at representable presheaf that the presheaf represented by an object $X$ of $C$ is the functor $h_X :C^{op} \to Set$ whose assignment is illustrated by

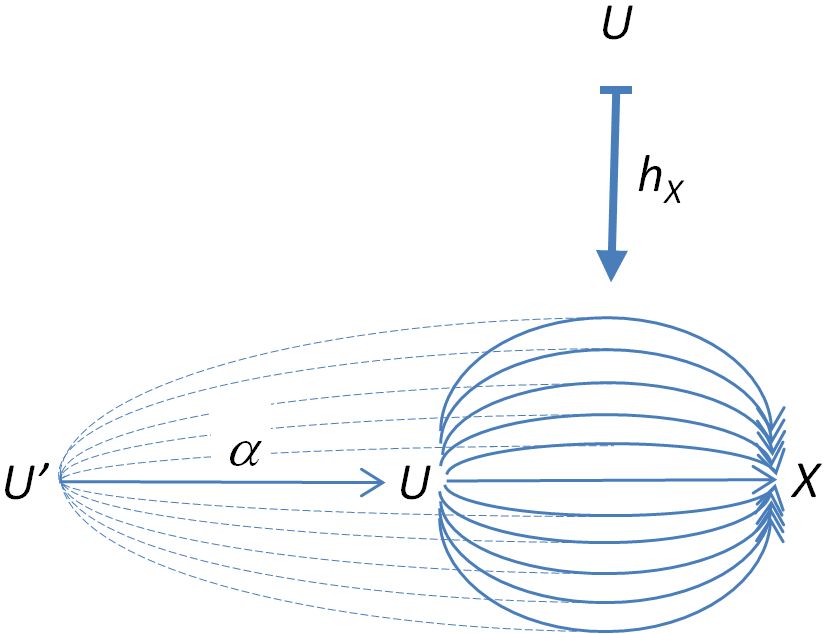
which sends each object $U$ to $Hom_C(U,X)$ and each morphism $\alpha:U'\to U$ to the function

$$h_X\alpha: Hom_C(U,X)\to Hom_C(U',X).$$

Moreover, for $f : X \to Y$ a morphism in $C$, this induces a natural transformation $h_f : h_X \to h_Y$, whose component on $U$ in $X$ is illustrated by

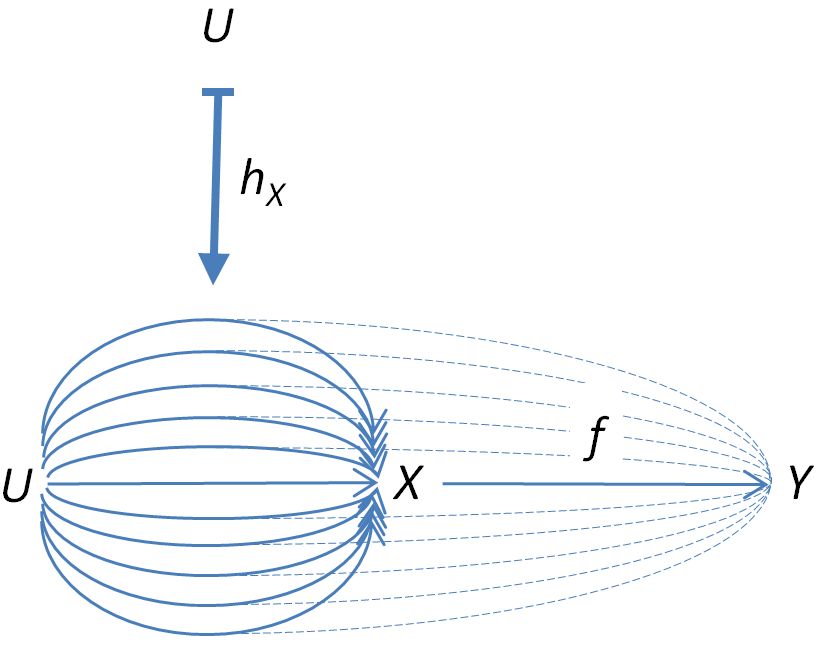
For this to be a natural transformation, we need to have the commuting diagram

$$\array{ h_X U & \stackrel{h_f U}{\rightarrow} & h_Y U \\ \mathllap{h_X\alpha\quad}{\downarrow} & {} & \mathrlap{\downarrow}{\quad h_Y\alpha} \\ h_X U' & \stackrel{h_f U'}{\rightarrow} & h_Y U' }$$

but this simply means that it doesn’t matter if we first “comb” the strands back to $U'$ and then comb the strands forward to $Y$, or comb the strands forward to $Y$ first and then comb the strands back to $U'$

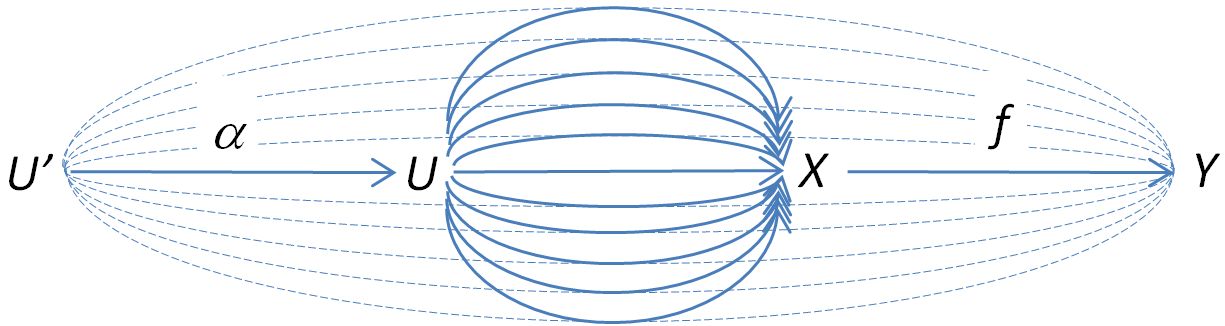
which follows from associativity of composition of morphisms in $C$.

Definition

The Yoneda embedding for $C$ a locally small category is the functor

$$Y : C \to [C^{op}, Set]$$

from $C$ to the category of presheaves over $C$ which is the image of the hom-functor

$$Hom : C^{op} \times C \to Set$$

under the Hom adjunction

$$Hom(C^{op} \times C , Set) \simeq Hom(C, [C^{op}, Set])$$

in the closed symmetric monoidal category Cat.

Hence $Y$ sends any object $c \in C$ to the representable presheaf which assigns to any other object $d$ of $C$ the hom-set of morphisms from $d$ into $c$:

$$Y(c) \;\colon\; C^{op} \stackrel{C(-,c)}{\to} Set \,.$$

The Yoneda embedding is sometimes denoted by よ, the hiragana for “Yo”; see the references below.

Remarks

We can also curry the Hom functor in the other variable, thus obtaining a contravariant functor

$$C^{op} \to [C, Set]$$

which is explicitly given by $c \mapsto C(c,-)$. This is sometimes jokingly called the contravariant Yoneda embedding.

However, since $C^{op}(-,c)=C(c,-)$, it is easy to see that the contravariant Yoneda embedding is just the Yoneda embedding $Y: C^{\op} \to [(C^{op})^{op}, Set]=[C, Set]$ of $C^{op}$, and hence does not require special treatment.

Properties

Proposition

(Yoneda embedding is a fully faithful functor)

For $\mathcal{C}$ any category, the functor

$$\array{ \mathcal{C} &\overset{Y}{\hookrightarrow}& [\mathcal{C}^{op}, Set] \\ c &\mapsto& Hom_{\mathcal{C}}(-,c) }$$

is fully faithful.

Proof

We need to show that for $c_1, c_2 \in \mathcal{C}$ any two objects, we have that every morphism of presheaves between their represented presheaves

$$Hom_{\mathcal{C}}(-,c_1) \overset{\phi}{\longrightarrow} Hom_{\mathcal{C}}(-,c_2)$$

is of the form

$$\phi \;=\; Hom_{\mathcal{C}}(-,f)$$

for a unique morphism

$$f \;\colon\; c_1 \to c_2$$

in $\mathcal{C}$. This follows by the Yoneda lemma, which says that morphisms $\phi$ as above are identified with the elements in

$$Hom_{\mathcal{C}}(-,c_2)(c_1) \;=\; Hom_{\mathcal{C}}(c_1,c_2) \,.$$

Proposition

The Yoneda embedding $y \colon \mathcal{C} \longrightarrow Func(\mathcal{C}^{op}, Set)$ preserves limits, hence is a continuous functor.

Proof

This follows because (1.) hom-functors preserve limits and (2.) limits of presheaves are computed objectwise:

$$\begin{array}{l} y\big( \underset{ \underset {i \in I} {\longleftarrow} }{\lim} \, c_i \big) \\ \;\equiv\; Hom\big( - ,\, \underset{ \underset {i \in I} {\longleftarrow} }{\lim} \, c_i \big) \\ \;\simeq\; \underset{ \underset {i \in I} {\longleftarrow} }{\lim} \, Hom\big( - ,\, c_i \big) \\ \;\simeq\; \underset{ \underset {i \in I} {\longleftarrow} }{\lim} \, y(c_i) \,. \end{array}$$

Remark

In contrast, the Yoneda embedding does not in general preserve colimits.

Instead, the Yoneda embedding of a small category $\mathcal{C}$ is its free cocompletion.

Remark

If the Yoneda embedding of a category has a left adjoint, then that category is called a total category .

Related concepts

• A category is a total category if its Yoneda embedding has a left adjoint.

• restricted Yoneda embedding

• (infinity,1)-Yoneda embedding

• singleton injection, the Yoneda embedding for 0-category theory.

• Yoneda lemma for bicategories

References

General

Named after Nobuo Yoneda (see at Yoneda lemma and the list of references given there).

Early accounts:

• Alexander Grothendieck, Section A.1 of: Technique de descente et théorèmes d’existence en géométrie algébriques. II. Le théorème d’existence en théorie formelle des modules, Séminaire Bourbaki : années 1958/59 - 1959/60, exposés 169-204, Séminaire Bourbaki, no. 5 (1960), Exposé no. 195, 22 p. (numdam:SB_1958-1960__5__369_0)

Notation

It seems that the notation “よ” for the Yoneda embedding (the hiragana for “Yo”) was first used in

• Theo Johnson-Freyd, Claudia Scheimbauer, p. 33 of (Op)lax natural transformations, twisted quantum field theories, and “even higher” Morita categories, (arxiv:1502.06526)

Their Latex code for the command reads as follows:

\usepackage[utf8]{inputenc}

\DeclareFontFamily{U}{min}{}

\DeclareFontShape{U}{min}{m}{n}{<-> udmj30}{}

\newcommand\yo{\!\text{\usefont{U}{min}{m}{n}\symbol{'207}}\!}

Subsequent references that use this notation include:

• Emily Riehl, Dominic Verity, p. 10 of Elements of $\infty$-category theory (web)

• David Li-Bland, p. 5 of The stack of higher internal categories and stacks of iterated spans (arXiv:1506.08870)

• Fosco Loregian, p. 4 of This is the (co)end, my only (co)friend (arXiv:1501.02503)

• Michael Hill, Michael Hopkins, Douglas Ravenel, p. 53 of Equivariant stable homotopy theory and the Kervaire invariant problem, (web)