nLab chord diagrams as multi-trace observables in BMN matrix model -- example

Chord diagrams as multi-trace observables in the BMN matrix model

The supersymmetric states of the BMN matrix model are temporally constant complex matrices which are complex metric Lie representations $\mathfrak{g} \otimes V \overset{\rho}{\to} V$ of $\mathfrak{g}=$su(2) (interpreted as fuzzy 2-sphere noncommutative geometries of giant gravitons or equivalently as fuzzy funnels of D0-D2 brane bound states).

A fuzzy 2-sphere-rotation invariant multi-trace observable on these supersymmetric states is hence an expression of the following form:

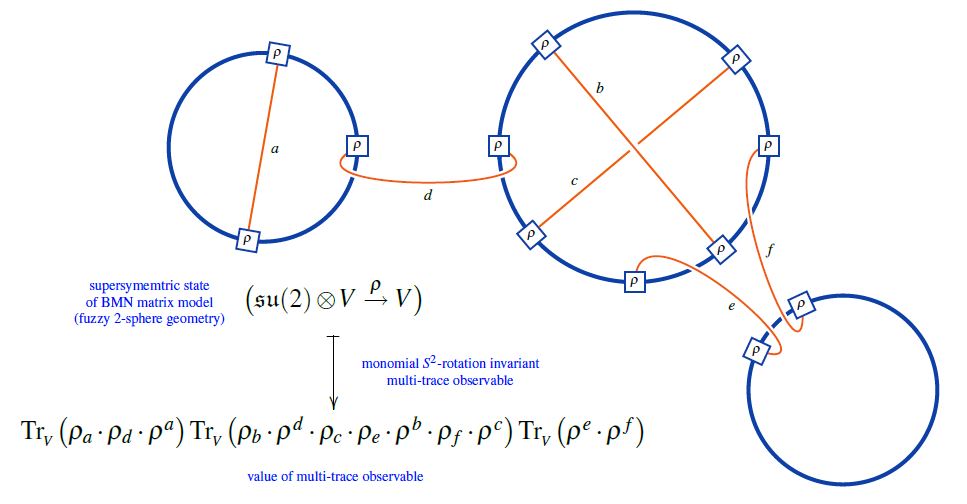
(from Sati-Schreiber 19c)

Here we are showing the corresponding string diagram/Penrose notation for metric Lie representations, which makes manifest that

1. these multi-trace observables are encoded by Sullivan chord diagrams $D$

2. their value on the supersymmetric states $\mathfrak{su}(2) \otimes V \overset{\rho}{\to}V$ is the evaluation of the corresponding Lie algebra weight system $w_{{}_V}$ on $D$.

Or equivalently, if $\widehat D$ is a horizontal chord diagram whose $\sigma$-permuted closure is $D$ (see here) then the values of the invariant multi-trace observables on the supersymmetric states of the BMN matrix model are the evaluation of $w_{V,\sigma}$ on $\widehat D$, as shown here:

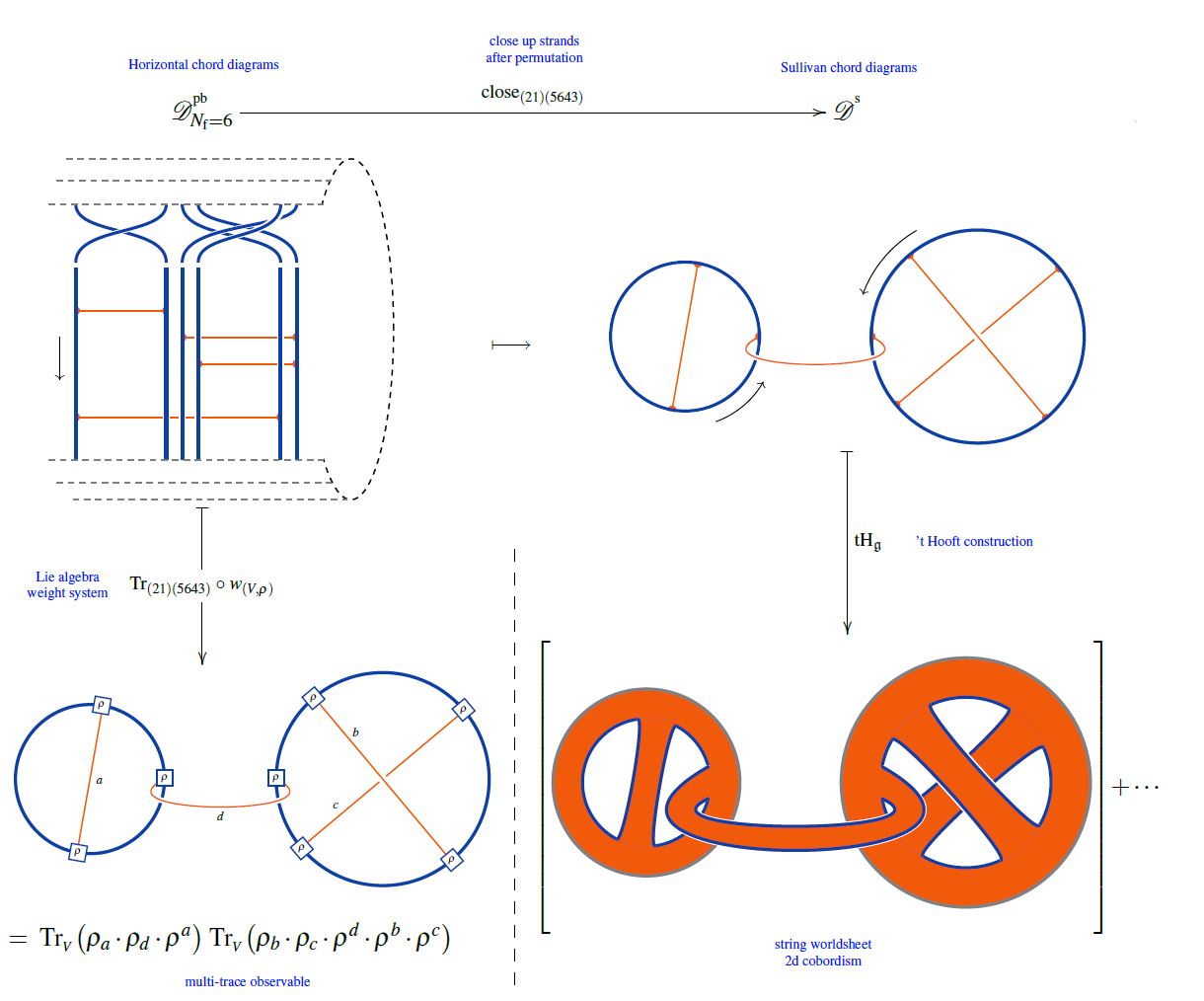
(from Sati-Schreiber 19c)

But since all horizontal weight systems are partitioned Lie algebra weight systems this way, this identifies supersymmetric states of the BMN matrix model as seen by invariant multi-trace observables as horizontal chord diagrams evaluated in Lie algebra weight systems.