nLab horizontal chord diagram
For discussion of standard round chord diagrams see at chord diagram.
Context
Graph theory
Properties
Extra properties
Extra structure
Knot theory
Examples/classes:
Types
Related concepts:
Contents
- Idea
- Defintions
- Monoid of horizontal chord diagrams
- Closure to round chord diagrams
- Algebra of horizontal chord diagrams
- The 2T- and 4T-relations
- Universal enveloping of infinitesimal braid relations
- Horizontal weight systems
- Star-algebra structure
- Closure to Sullivan chord diagrams
- Applications
- Related concepts
- References
Idea
A horizontal chord diagram on strands is a finite undirected graph that is obtained from a trivalent graph with numbered embedded disjoint circles by cutting the circles open (to give the strands), such that the result has all edges not inside the circles (the chords) be vertically ordered (i.e. along the strands) and going between distinct strands.
Here is an example of a horizontal chord diagram on 5 strands:
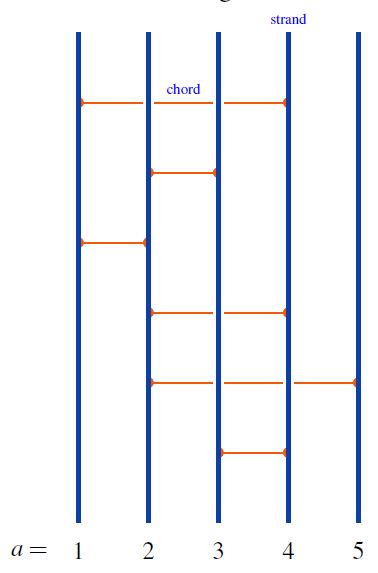
graphics from Sati-Schreiber 19c
Defintions
Monoid of horizontal chord diagrams
For (the number of strands), the monoid of horizontal chord diagrams is the free monoid
on the set of pairs of distinct elements of , i.e. of pairs of strands, called the chords (the traditional superscript is for pure braids).
Hence a horizontal chord diagram is equivalently a finite list of chords
and the product of chord diagrams is the concatenation of these list, with the empty list being the neutral element.
The function that sends the chord to that permutation of elements (strands) which is given by the transposition of the th with the th strand extends to a unique monoid homomorphism from the monoid of horizontal chord diagrams (1) to the symmetric group on elements:
Closure to round chord diagrams
Given a horizontal chord diagram on strands and given any choice of cyclic permutation of elements, the trace of horizontal to round chord diagrams is the round chord diagram obtained by gluing the ends of the strands according to the cyclic permutation, and retaining the chords in the evident way.
The following shows an example of the trace operation for cyclic permutation of strands one step to the left:
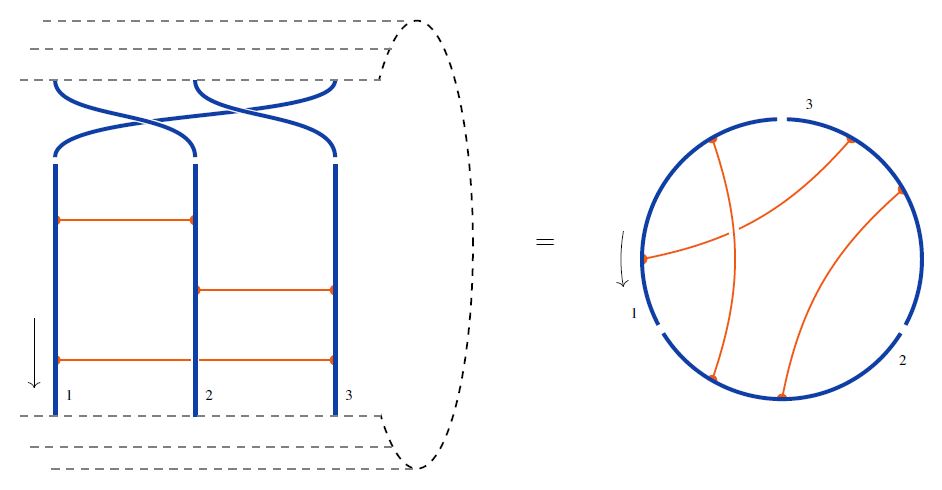
graphics from Sati-Schreiber 19c
The following are the analogous traces of the four types of horizontal chord diagrams appearing in the 4T relation:
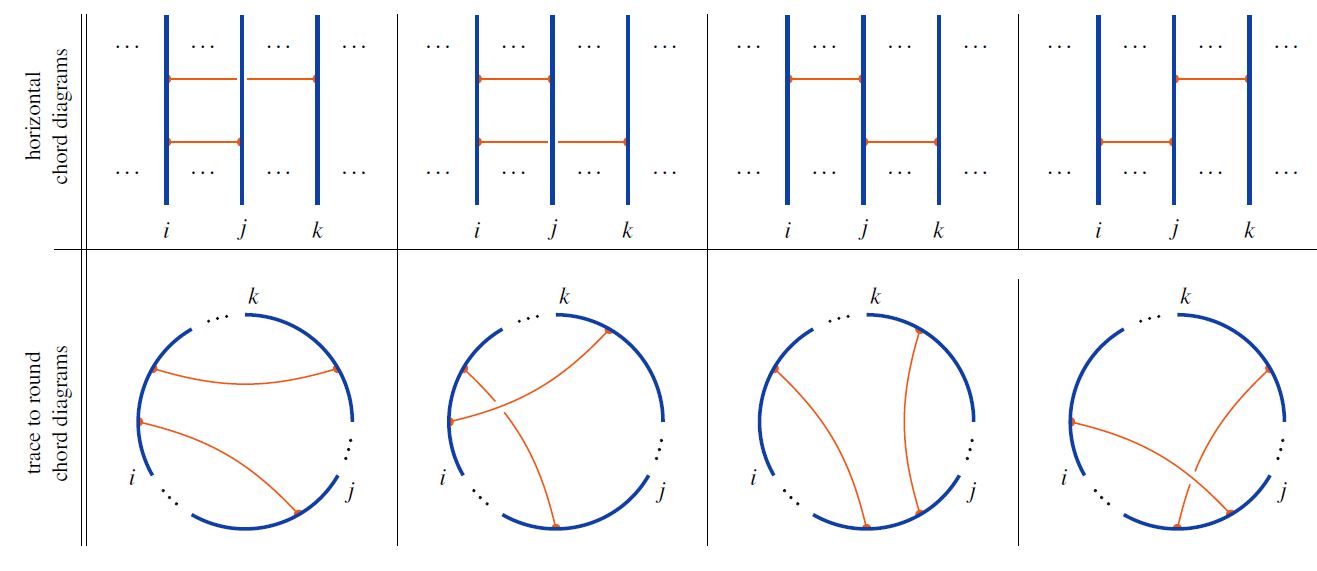
graphics from Sati-Schreiber 19c
This defines a function
from the set of horizontal chord diagrams to the set of round chord diagrams.
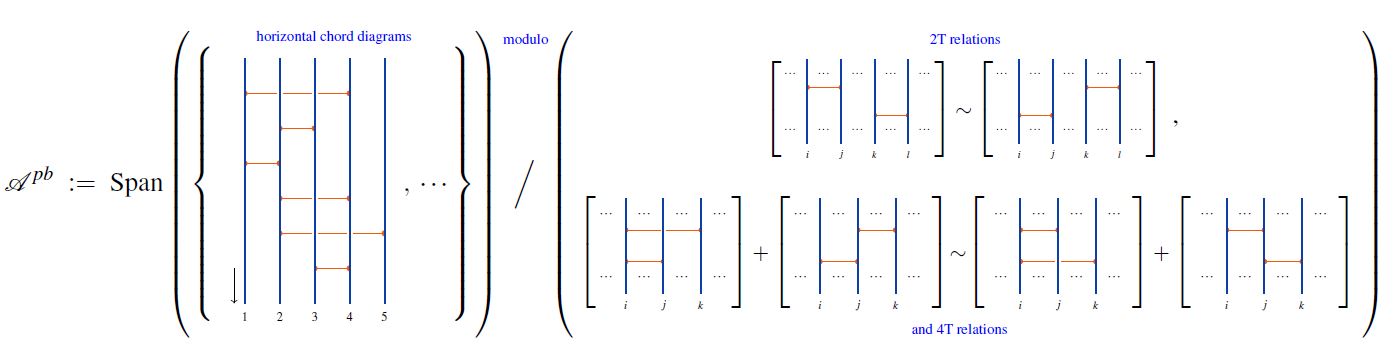
Algebra of horizontal chord diagrams
Definition
For and for , the linear span on the set of horizontal chord diagrams on strands becomes an graded associative algebra
under concatenation of strands.
For example:
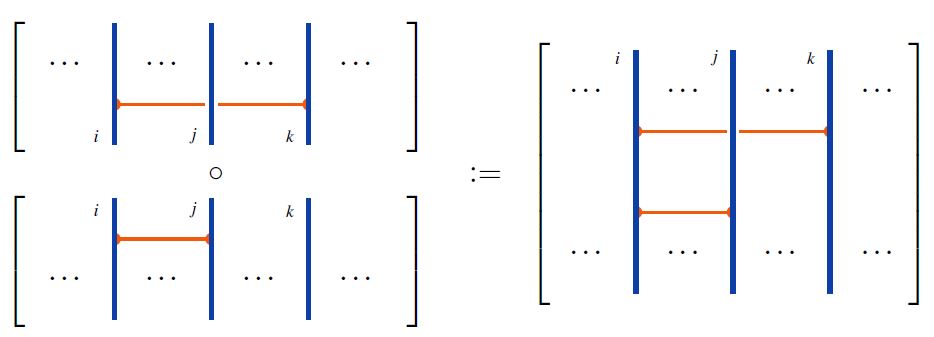
The 2T- and 4T-relations
Definition
On the -module of horizontal chord diagrams consider the following relations:
The 2T relations – for pairwise distinct indices the -chord commutes with the -chord, for instance:
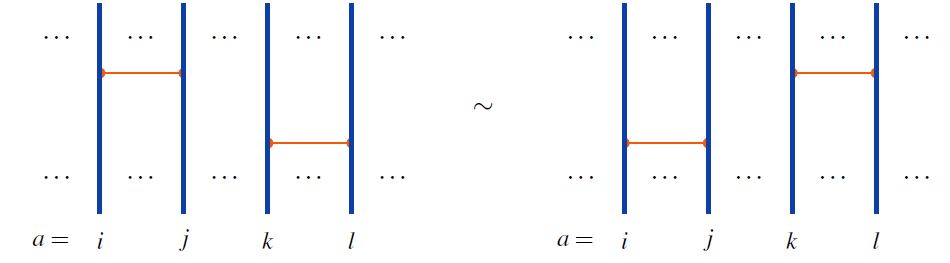
and the 4T relations – for pairwise distinct indices we have:
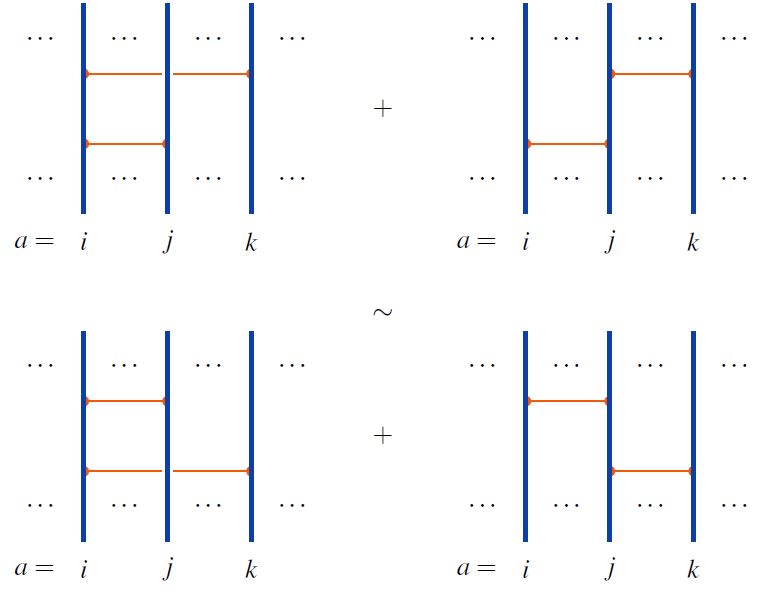
graphics from Sati-Schreiber 19c
In terms of the commutator Lie algebra of the above algebra of horizontal chord diagrams, these are the infinitesimal braid relations.
One writes
for the quotient algebra of horizontal chord diagrams by these relations.
Universal enveloping of infinitesimal braid relations
Proposition
(universal enveloping algebra of infinitesimal braid Lie algebra is horizontal chord diagrams modulo 2T&4T)
of horizontal chord diagrams on strands with product given by concatenation of strands (Def. ) modulo the 2T relations and 4T relations (Def. ) is isomorphic to the universal enveloping algebra of the infinitesimal braid Lie algebra (this Def.):
Horizontal weight systems
An -linear map from the quotient module (2) of horizontal chord diagrams to
is called a weight system on horizontal chord diagrams (of strands), or maybe a horizontal weight systems.
Hence for a field, the vector space of all horizontal weight systems is the degreewise dual vector space
Star-algebra structure
Over a ground ring that is itself equipped with the structure of a star-algebra (such as the real numbers, trivially, or the complex numbers via complex conjugation), we have that also the associative algebra (2)
of horizontal chord diagrams on strands with product given by concatenation of strands (Def. ) modulo the 2T relations and 4T relations (Def. )
becomes a star-algebra with star-operation
given by reversing the orientation of strands:
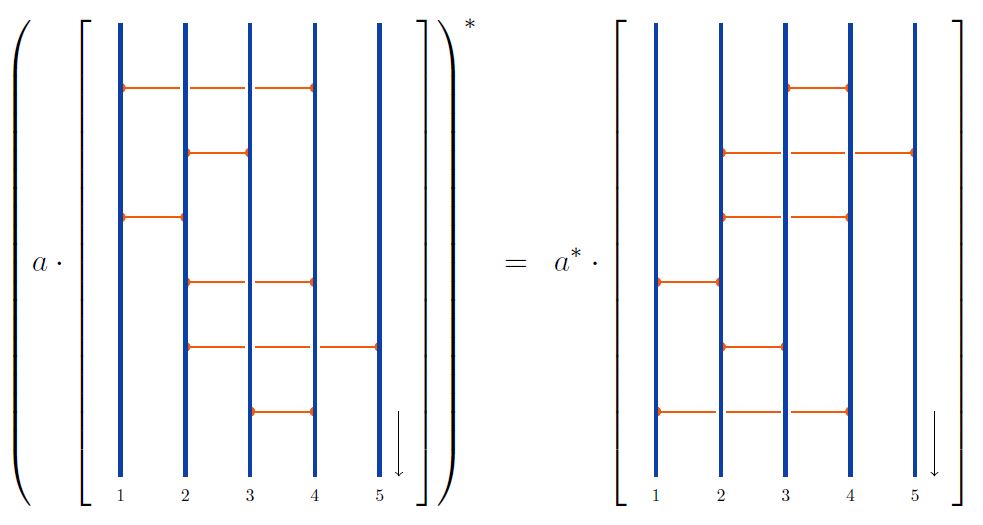
Since horizontal chord diagrams are the homology of the loop space of configuration space and the homology of a loop space is an involutive Hopf algebra, this is a special case of the general fact that involutive Hopf algebras are star-algebras (here).
With respect to this star-algebra-structure one may ask (setting for definiteness) whether a given weight system (3)
is a state on a star-algebra in that for any we have that the value of on the corresponding normal operator is a non-negative real number:
The weight systems which are states on a star-algebra with respect to this star-involution are discussed in CSS 21.
Closure to Sullivan chord diagrams
More generally, one obtains Sullivan chord diagrams with disjoint embedded circles from horizontal chord diagrams by closing up strands after acting with a permutation with cycles ( orbits)
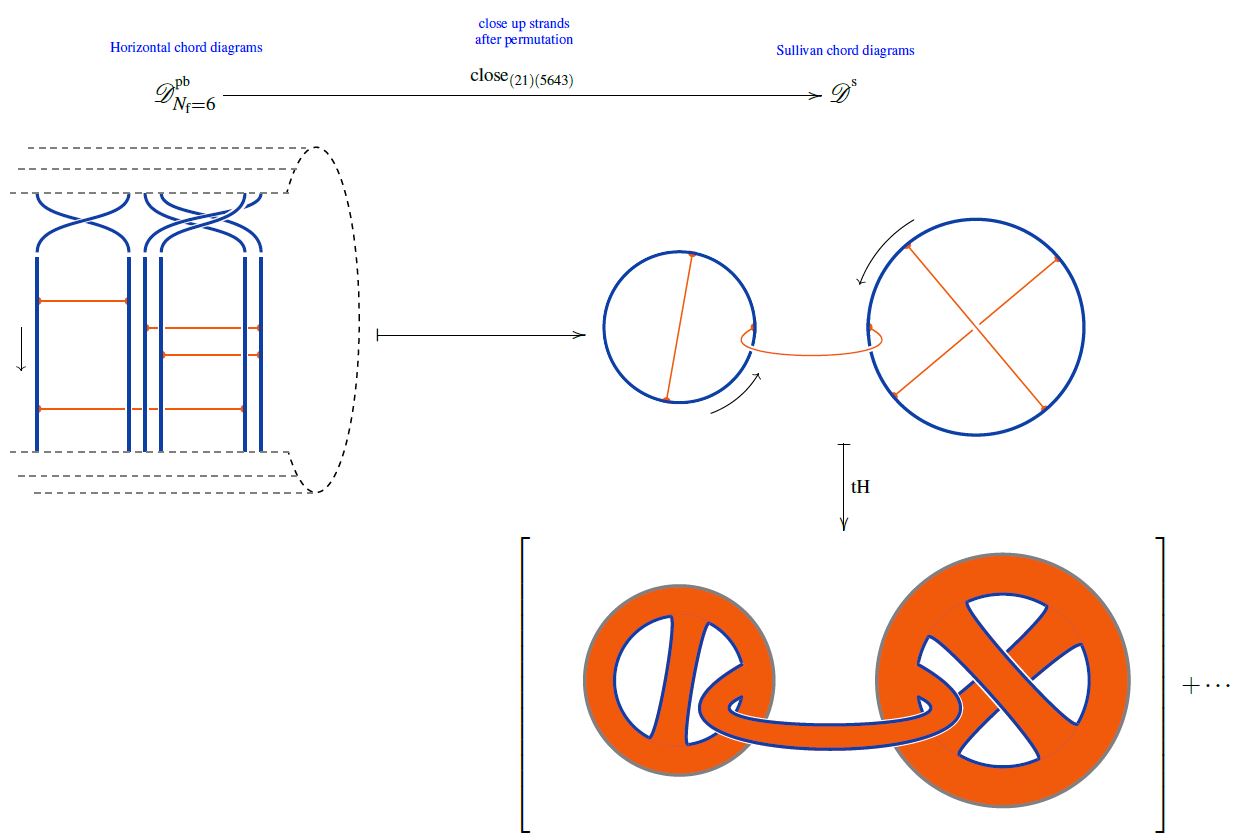
from Sati-Schreiber 19c
Applications
Knizhnik-Zamolodchicov connection
For the Definition of the Knizhnik-Zamolodchikov connection we need the following notation:
-
configuration spaces of points
For write
(4)for the ordered configuration space of n points in the plane, regarded as a smooth manifold.
Identifying the plane with the complex plane , we have canonical holomorphic coordinate functions
(5) -
(6)
for the quotient vector space of the linear span of horizontal chord diagrams on strands by the 4T relations (infinitesimal braid relations), regarded as an associative algebra under concatenation of strands (here).
Definition
The universal Knizhnik-Zamolodchikov form is the horizontal chord diagram-algebra valued differential form (6) on the configuration space of points (4)
given in the canonical coordinates (5) by:
where

is the horizontal chord diagram with exactly one chord, which stretches between the th and the th strand.
Regarded as a connection form for a connection on a vector bundle, this defines the universal Knizhnik-Zamolodchikov connection , with covariant derivative
for any smooth function
with values in modules over the algebra of horizontal chord diagrams modulo 4T relations.
The condition of covariant constancy
is called the Knizhnik-Zamolodchikov equation.
Finally, given a metric Lie algebra and a tuple of Lie algebra representations
the corresponding endomorphism-valued Lie algebra weight system
turns the universal Knizhnik-Zamolodchikov form (7) into a endomorphism ring-valued differential form
The universal formulation (7) is highlighted for instance in Bat-Natan 95, Section 4.2, Lescop 00, p. 7. Most authors state the version after evaluation in a Lie algebra weight system, e.g. Kohno 14, Section 5.
Proposition
(Knizhnik-Zamolodchikov connection is flat)
The Knizhnik-Zamolodchikov connection (Def. ) is flat:
Proposition
(Kontsevich integral for braids)
The Dyson formula for the holonomy of the Knizhnik-Zamolodchikov connection (Def. ) is called the Kontsevich integral on braids.
(e.g. Lescop 00, side-remark 1.14)
Chord diagrams as multi-trace observables in the BMN matrix model
The supersymmetric states of the BMN matrix model are temporally constant complex matrices which are complex metric Lie representations of su(2) (interpreted as fuzzy 2-sphere noncommutative geometries of giant gravitons or equivalently as fuzzy funnels of D0-D2 brane bound states).
A fuzzy 2-sphere-rotation invariant multi-trace observable on these supersymmetric states is hence an expression of the following form:
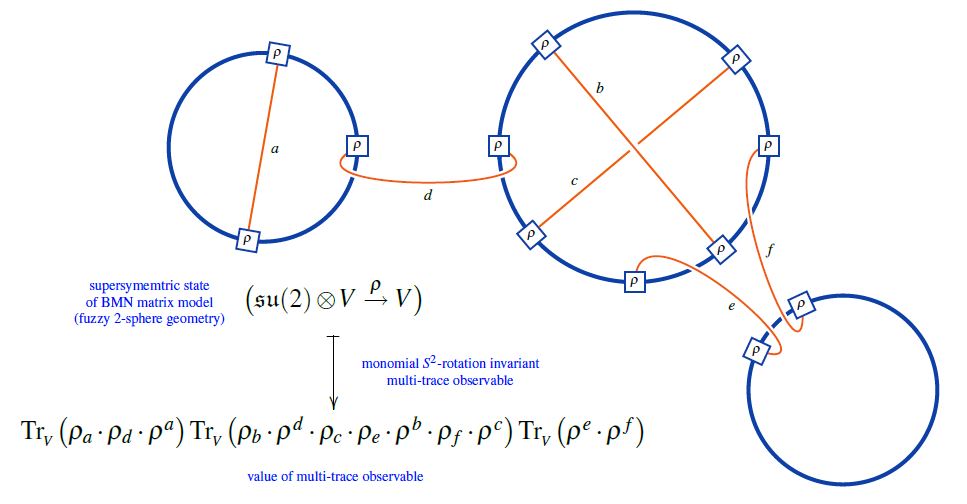
(from Sati-Schreiber 19c)
Here we are showing the corresponding string diagram/Penrose notation for metric Lie representations, which makes manifest that
-
these multi-trace observables are encoded by Sullivan chord diagrams
-
their value on the supersymmetric states is the evaluation of the corresponding Lie algebra weight system on .
Or equivalently, if is a horizontal chord diagram whose -permuted closure is (see here) then the values of the invariant multi-trace observables on the supersymmetric states of the BMN matrix model are the evaluation of on , as shown here:
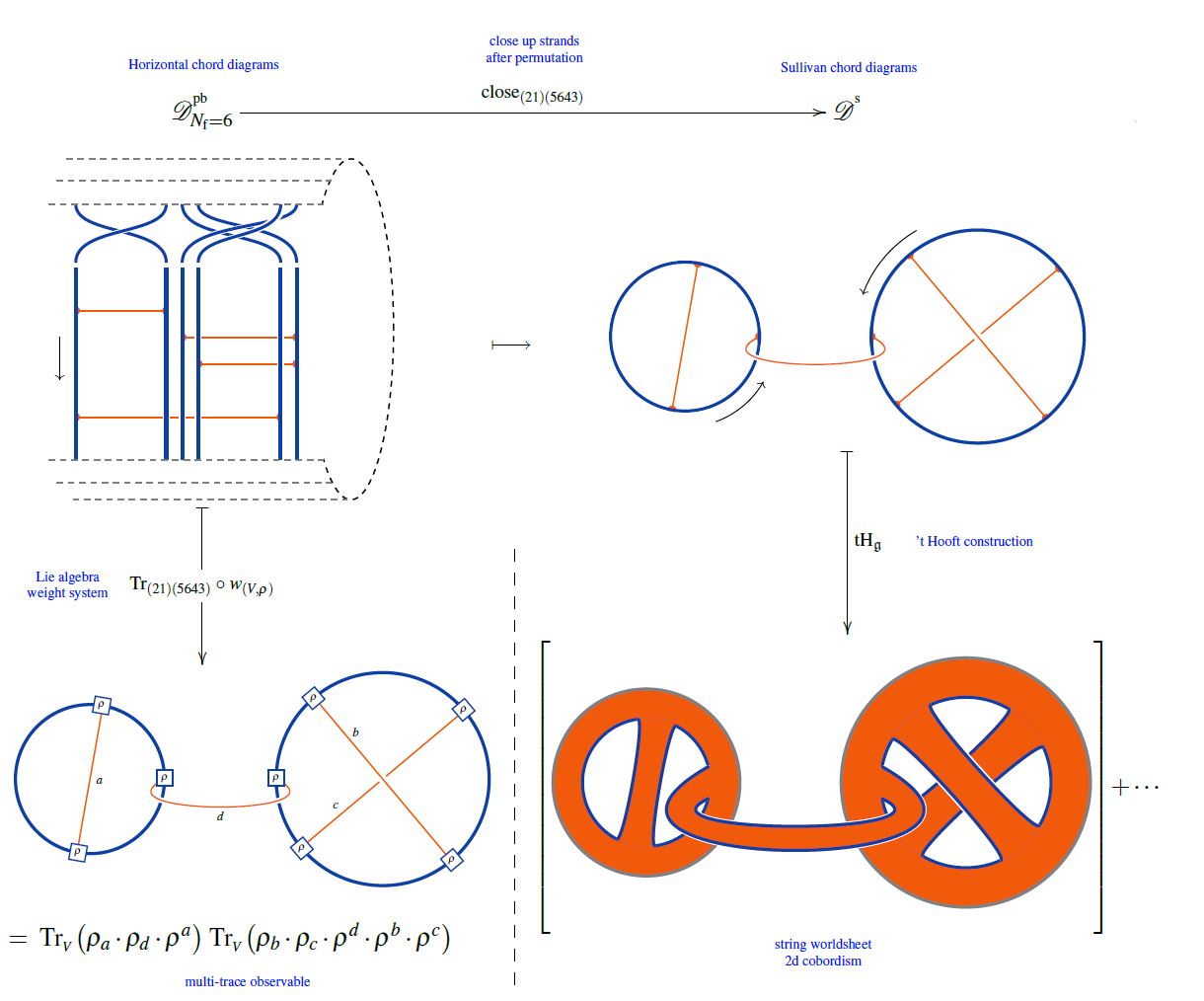
(from Sati-Schreiber 19c)
But since all horizontal weight systems are partitioned Lie algebra weight systems this way, this identifies supersymmetric states of the BMN matrix model as seen by invariant multi-trace observables as horizontal chord diagrams evaluated in Lie algebra weight systems.
Related concepts
| chord diagrams | weight systems |
|---|---|
| linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams | Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems |
References
Original articles:
-
Dror Bar-Natan, Vassiliev and Quantum Invariants of Braids, Geom. Topol. Monogr. 4 (2002) 143-160 (arxiv:q-alg/9607001)
-
Toshitake Kohno, Loop spaces of configuration spaces and finite type invariants, Geom. Topol. Monogr. 4 (2002) 143-160 (arXiv:math/0211056)
-
Adrien Brochier, Cyclotomic associators and finite type invariants for tangles in the solid torus, Algebr. Geom. Topol. 13 (2013) 3365-3409 (arXiv:1209.0417)
Textbook accounts:
- Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Section 5.11 of: Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv:1103.5628, doi:10.1017/CBO9781139107846)
Discussion of the star-algebra-structure and associated states on horizontal chord diagrams:
Last revised on September 9, 2023 at 08:07:15. See the history of this page for a list of all contributions to it.