nLab string diagram
Context
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Higher category theory
Basic concepts
Basic theorems
-
homotopy hypothesis-theorem
-
delooping hypothesis-theorem
-
stabilization hypothesis-theorem
Applications
Models
- (n,r)-category
- Theta-space
- ∞-category/∞-category
- (∞,n)-category
- (∞,2)-category
- (∞,1)-category
- (∞,0)-category/∞-groupoid
- (∞,Z)-category
- n-category = (n,n)-category
- n-poset = (n-1,n)-category
- n-groupoid = (n,0)-category
- categorification/decategorification
- geometric definition of higher category
- algebraic definition of higher category
- stable homotopy theory
Morphisms
Functors
Universal constructions
Extra properties and structure
1-categorical presentations
String diagrams
Idea
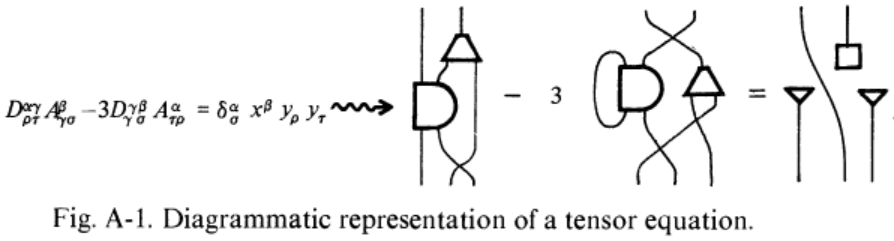
String diagrams constitute a graphical calculus for expressing operations in monoidal categories.
In the archetypical case of the Cartesian monoidal category of finite sets this is Hotz’s notation (Hotz 65) for automata, while for finite-dimensional vector spaces with their usual tensor product this is Penrose’s notation (Penrose 71a, Penrose-Rindler 84) for tensor networks; but the same idea immediately applies more generally to any other monoidal category and yet more generally to bicategories, etc.
The idea is roughly to think of objects in a monoidal category as “strings” and of morphisms from one tensor product to another as a node which the source strings enter and the target strings exit. Further structure on the monoidal category is encoded in geometrical properties on these strings.
For instance:
-
putting strings next to each other denotes the monoidal product, and having no string at all denotes the tensor unit;
-
braiding strings over each other corresponds to – yes, the monoidal braiding (if any);
-
bending strings around corresponds to dualities on dualizable objects (if any).
Many operations in monoidal categories that look unenlightening in symbols become obvious in string diagram calculus, such as the trace: an output wire gets bent around and connects to an input.
String diagrams may be seen as dual (in the sense of Poincaré duality) to commutative diagrams. For instance, in a 2-category, an example of a string diagram for a 2-morphism (shown on the left) is shown on the right here:
String diagrams for monoidal categories can be obtained in the same way, by considering a monoidal category as a 2-category with a single object.
Variants
There are many additional extra structures on monoidal categories, or similar structures, which can usually be represented by encoding further geometric properties of their string diagram calculus For instance:
-
in monoidal categories which are ribbon categories the strings from above behave as if they have a small transversal extension which makes them behave as ribbons. Accordingly, there is a twist operation in the axioms of a ribbon category and graphically it corresponds to twisting the ribbons by 360 degrees.
-
in a traced monoidal category, the trace can be represented by bending an output string around to connect to an input, even though if the objects are not dualizable the individual “bends” do not represent anything.
-
in monoidal categories which are spherical all strings behave as if drawn on a sphere.
-
in a hypergraph category, the string diagrams are labeled hypergraphs.
-
string diagrams can be extended to represent monoidal functors in several ways. One nice way is described in these slides, and can also be done with “3D regions” as drawn here.
-
there is also a string diagram calculus for bicategories, which extends that for monoidal categories regarded as one-object bicategories. Thus, the strings now represent 1-cells and the nodes 2-cells, leaving the two-dimensional planar regions cut out by the strings to represent the 0-cells. This makes it manifest that in general, string diagram notation is Poincaré dual to the globular notation: where one uses -dimensional symbols, the other uses -dimensional symbols.
-
string diagrams for bicategories can be generalized to string diagrams for double categories and proarrow equipments by distinguishing between “vertical” and “horizontal” strings.
-
One can also categorify string diagrams to “surface diagrams”, which are dual to commutative diagrams in 3-categories (including monoidal bicategories, and braided monoidal categories.
-
Yet more generally, one can categorify string diagrams to diagrams that are dual to commutative diagrams in -categories, which yields the notion of manifold -diagrams.
-
As explained here, in the presence of certain levels of duality it may be better to work with diagrams on cylinders or spheres rather than in boxes. This relates to planar algebras and canopolises?.
-
A string diagram calculus for monoidal fibrations can be obtained as a generalization of C.S. Peirce’s “existential graphs.” The ideas are essentially contained in (Brady-Trimble 98) and developed in (Ponto-Shulman 12), and was discussed here.
-
String diagrams for closed monoidal categories (see also at Kelly-Mac Lane graph) are similar to those for autonomous categories, but a bit subtler, involving “boxes” to separate parts of the diagram. They were used informally by Baez and Stay here and here, but can also be done in essentially the same way as the proof nets used in intuitionistic linear logic; see Lamarche.
-
Proof nets for multiplicative linear logic with negation similarly give string diagrams for *-autonomous categories, or more generally linearly distributive categories; see Blute-Cockett-Seely-Trimble.
-
Proof surfaces for noncommutative multiplicative linear logic with negation, see Dunn-Vicary
-
Sheet diagrams, string diagrams drawn on a branching surface, may be used for rig categories, see Comfort-Delpeuch-Hedges.
See also Selinger 09 for a review of different string diagram formalisms.
Examples
In linear algebra
String diagram calculus in linear algebra:
-
String diagrams in finite-dimensional vector spaces with the usual tensor product are Penrose’s notation (Penrose 71a, 71b, 72, Penrose-Rindler 84, Append.) for working with tensors.
-
More recently, string diagrams in this category have come to be known as tensor networks, especially so in application to condensed matter physics and also in quantum computation and in particular in quantum error correction.
In quantum computation
- In quantum computation, quantum circuit diagrams are a form of string diagrams in finite-dimensional Hilbert spaces. See also at finite quantum mechanics in terms of dagger-compact categories.
In representation theory
String diagram calculus in representation theory: Mandula 81, Cvitanović 08
- String diagrams for the monoidal category of finite-dimensional linear representations of the group SU(2) on complex vector spaces are called spin networks.
In Lie theory
For string diagrams calculus in Lie theory see at:
In perturbative quantum field theory
For applications of string diagram calculus in perturbative quantum field theory, see at
(…)
Related concepts
References
Introduction and survey
Discussion in representation theory:
-
Jeffrey Ellis Mandula, Diagrammatic techniques in group theory, Southampton Univ. Phys. Dept. (1981) (cds:129911, pdf)
-
Predrag Cvitanović, Group Theory: Birdtracks, Lie’s, and Exceptional Groups, Princeton University Press July 2008 (PUP, birdtracks.eu, pdf)
(aimed at Lie theory and gauge theory)
-
Stéphane Peigné, Introduction to color in QCD: Initiation to the birdtrack pictorial technique [arXiv:2302.07574]
(further focus on QCD)
Introductions to and surveys of string diagram calculus:
-
Ross Street, Categorical structures, in: M. Hazewinkel (ed.), Handbook of algebra – Volume 1, Elsevier (1996) [pdf, 978-0-444-82212-3]
(in the generality of bicategories)
-
Ross Street, Low dimensional topology and higher-order categories (ps)
(on surface diagrams)
-
John Baez, QG Seminar Fall 2000 [web), Winter 2001 (web), Fall 2006 (web]
-
The Catsters: String Diagrams, video lectures (2008) [playlist: YT]
-
John Baez, Mike Stay: Physics, Topology, Logic and Computation: A Rosetta Stone, in: New Structures for Physics, Lecture Notes in Physics 813 Springer (2011) 95-174 [arXiv:0903.0340, doi:10.1007/978-3-642-12821-9_2]
-
Peter Selinger, A survey of graphical languages for monoidal categories, in: Bob Coecke (ed.) New Structures for Physics, Lecture Notes in Physics, vol 813. Springer, Berlin, Heidelberg (2010) (arXiv:0908.334, doi:10.1007/978-3-642-12821-9_4)
-
Joseph M. Landsberg, §2.11 in: Tensors: Geometry and Applications, Graduate Studies in Mathematics 128, American Mathematical Society (2011) [ISBN:978-0-8218-6907-9, ams:gsm-128]
-
Aleks Kissinger, Pictures of Processes: Automated Graph Rewriting for Monoidal Categories and Applications to Quantum Computing (arXiv:1203.0202)
-
Robin Piedeleu, Fabio Zanasi: An Introduction to String Diagrams for Computer Scientists, Cambridge University Press (2025) [arXiv:2305.08768, doi:10.1017/9781009625715]
(in computer science)
From the point of view of finite quantum mechanics in terms of dagger-compact categories:
-
Bob Coecke, Quantum Picturalism (arXiv:0908.1787)
-
Bob Coecke, Introducing categories to the practicing physicist (arXiv:0808.1032)
-
Bob Coecke, Categories for the practising physicist (arXiv:0905.3010)
-
Bob Coecke, Ross Duncan, Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 (arXiv:0906.4725)
-
Chris Heunen, Jamie Vicary, Lectures on categorical quantum mechanics, 2012 (pdf)
From the point of view of tensor networks in solid state physics:
-
Jacob Biamonte, Ville Bergholm, Tensor Networks in a Nutshell, Contemporary Physics (arxiv:1708.00006)
-
Jacob Biamonte, Lectures on Quantum Tensor Networks (arXiv:1912.10049)
Some philosophical discussion is given in
- David Corfield, Section 10.4 of: Towards a Philosophy of Real Mathematics, CUP, 2003.
Original articles
The development and use of string diagram calculus pre-dates its graphical appearance in print, due to the difficulty of printing non-text elements at the time.
Many calculations in earlier works were quite clearly worked out with string diagrams, then painstakingly copied into equations. Sometimes, clearly graphical structures were described in some detail without actually being drawn: e.g. the construction of free compact closed categories in Kelly and Laplaza’s 1980 “Coherence for compact closed categories”.
(Pawel Sobocinski, 2 May 2017)
This idea that string diagrams are, due to technical issues, only useful for private calculation, is said explicitly by Penrose. Penrose and Rindler’s book “Spinors and Spacetime” (CUP 1984) has an 11-page appendix full of all sorts of beautiful, carefully hand-drawn graphical notation for tensors and various operations on them (e.g. anti-symmetrization and covariant derivative). On the second page, he says the following:
“The notation has been found very useful in practice as it grealy simplifies the appearance of complicated tensor or spinor equations, the various interrelations expressed being discernable at a glance. Unfortunately the notation seems to be of value mainly for private calculations because it cannot be printed in the normal way.”
The first formal definition of string diagrams in the literature appears to be in
- Günter Hotz, Eine Algebraisierung des Syntheseproblems von Schaltkreisen, EIK, Bd. 1, (185-205), Bd, 2, (209-231) 1965 (part I, part II, pdf)
Application of string diagrams to tensor-calculus in mathematical physics (hence for the case that the ambient monoidal category is that of finite dimensional vector spaces equipped with the tensor product of vector spaces) was propagated by Roger Penrose, whence physicists know string diagrams as Penrose notation for tensor calculus:
-
Roger Penrose, Applications of negative dimensional tensors, Combinatorial Mathematics and its Applications, Academic Press (1971) (pdf, pdf)
-
Roger Penrose, Angular momentum: An approach to combinatorial spacetime, in Ted Bastin (ed.) Quantum Theory and Beyond, Cambridge University Press (1971), pp.151-180 (pdf)
-
Roger Penrose, On the nature of quantum geometry, in: J. Klauder (ed.) Magic Without Magic, Freeman, San Francisco, 1972, pp. 333–354 (spire:74082, pdf)
-
Roger Penrose, Wolfgang Rindler, appendix (p. 424-434) of: Spinors and space-time – Volume 1: Two-spinor calculus and relativistic fields, Cambridge University Press 1984 (doi:10.1017/CBO9780511564048)
See also
- Wikipedia, Penrose graphical notation
From the point of view of monoidal category theory, an early description of string diagram calculus (without actually depicting any string diagrams, see the above comments) is in:
-
Max Kelly, M. L. Laplaza, Coherence for compact closed categories, Journal of Pure and Applied Algebra, 19 193-213 (1980) [doi:10.1016/0022-4049(80)90101-2, pdf]
(proving the coherence for compact closed categories)
following
-
Max Kelly, Many-variable functorial calculus I, in: Max Kelly, M. Laplaza , L. Gaunce Lewis, Jr., Saunders Mac Lane (eds.) Coherence in Categories, Lecture Notes in Mathematics, vol 281. Springer, Berlin, Heidelberg 1972 (doi:10.1007/BFb0059556)
(which does include the hand-drawn diagrams that are missing in Kelly-Laplaza 80!)
and in
-
André Joyal, Ross Street: The geometry of tensor calculus I_, Advances in Math. 88 (1991) 55-112; MR92d:18011 [pdf, doi:10.1016/0001-8708(91)90003-P]
-
André Joyal and Ross Street, The geometry of tensor calculus II (pdf)
String diagram calculus was apparently popularized by its use in
-
Louis Kauffman, Knots and physics, Series on Knots and Everything, Volume 1, World Scientific, 1991 (doi:10.1142/1116)
(in the context of knot theory)
Probably David Yetter was the first (at least in public) to write string diagrams with “coupons” (a term used by Nicolai Reshetikhin and Turaev a few months later) to represent maps which are not inherent in the (braided or symmetric compact closed) monoidal structure.
See also these:
-
Peter Freyd, David Yetter, Braided compact closed categories with applications to low dimensional topology Advances in Mathematics, 77:156–182, 1989.
-
Peter Freyd and David Yetter, Coherence theorems via knot theory. Journal of Pure and Applied Algebra, 78:49–76, 1992.
-
David Yetter, Framed tangles and a theorem of Deligne on braided deformations of tannakian categories In M. Gerstenhaber and Jim Stasheff (eds.) Deformation Theory and Quantum Groups with Applications to Mathematical Physics, Contemporary Mathematics 134, pages 325–349. Americal Mathematical Society, 1992.
-
Paul-André Melliès, Functorial boxes in string diagrams, Procceding of Computer Science Logic 2006 in Szeged, Hungary. 2006 (hal:00154243, pdf, pdf)
(see also computational trilogy)
For more on the history of the notion see the bibliography in (Selinger 09).
Details
String diagrams for monoidal categories are discussed in:
-
Andre Joyal and Ross Street, The geometry of tensor calculus I, Advances in Math. 88 (1991) 55-112; MR92d:18011. (pdf)
-
Andre Joyal and Ross Street, The geometry of tensor calculus II. (pdf.
-
Andre Joyal and Ross Street, Planar diagrams and tensor algebra, available here.
and for discussion of coherence and strictification for symmetric monoidal categories:
- Paul Wilson, Dan Ghica, Fabio Zanasi: String Diagrams for Strictification and Coherence, Logical Methods in Computer Science (2024) [arXiv:2201.11738]
For 1-categories in
-
Dan Marsden, Category Theory Using String Diagrams, (arXiv:1401.7220).
(therein: many explicit calculations, colored illustrations, avoiding the common practice of indicating 0-cells by non-filled circles)
For traced monoidal categories in
-
Andre Joyal, Ross Street and Verity, Traced monoidal categories.
-
David I. Spivak, Patrick Schultz, Dylan Rupel, String diagrams for traced and compact categories are oriented 1-cobordisms, arxiv
For closed monoidal categories in
-
John Baez and Mike Stay, Physics, Topology, Logic and Computation: A Rosetta Stone, arxiv
-
Francois Lamarche, Proof Nets for Intuitionistic Linear Logic: Essential nets, 2008 pdf
-
Ralf Hinze, Kan Extensions for Program Optimisation, Or: Art and Dan Explain an Old Trick, pdf
-
Dan Ghica, Fabio Zanasi, String Diagrams for λ-calculi and Functional Computation [arXiv:2305.18945]
For biclosed monoidal categories in
- Bob Coecke, Edward Grefenstette, and Mehrnoosh Sadrzadeh, Lambek vs. Lambek: Functorial vector space semantics and string diagrams for Lambek calculus, 2013 link
For linearly distributive categories in
- Richard Blute and Robin Cockett and R.A.G. Seely and Todd Trimble, Natural deduction and coherence for weakly distributive categories.
- Lawrence Dunn, Jamie Vicary, Surface Proofs for Nonsymmetric Linear Logic (arXiv:1701.04917)
For indexed monoidal categories in
-
Geraldine Brady, Todd Trimble, A string diagram calculus for predicate logic (1998)
-
Kate Ponto, Michael Shulman, Duality and traces for indexed monoidal categories, Theory and Applications of Categories, Vol. 26, 2012, No. 23, pp 582-659 (arXiv:1211.1555)
For symmetric traced monoidal categories in
- George Kaye, The Graphical Language of Symmetric Traced Monoidal Categories, (arXiv:2010.06319)
Further elaboration on the method of Joyal & Street 1991:
-
Sen Hu, Xuexing Lu, Yu Ye: A graphical calculus for semi-groupal categories, Appl Categor Struct 27 (2019) 163–197 [arXiv:1604.07276, doi:10.1007/s10485-018-9549-8]
-
Xuexing Lu, Yu Ye: Combinatorial characterization of upward planarity, Commun. Math. Stat. 7 (2019) 207–223 [arXiv:1608.07255, doi:10.1007/s40304-018-0169-2]
The generalization of string diagrams to one dimension higher is discussed in
-
John Barrett, Catherine Meusburger, Gregor Schaumann, Gray categories with duals and their diagrams, available here.
The generalization to arbitrary dimension in terms of opetopic “zoom complexes” is due to
- Joachim Kock, André Joyal, Michael Batanin, Jean-François Mascari, Polynomial functors and opetopes (arXiv:0706.1033)
The generalization to arbitrary dimension in terms of manifold diagrams (generalizing, in particular, opetopic shapes) is due to
- Christoph Dorn and Christopher Douglas, Manifold diagrams and tame tangles, 2022 (arXiv, latest)
Discussion of string diagram calculus for (virtual) double categories and (virtual) pro-arrow equipments:
-
David Jaz Myers, String Diagrams For Double Categories and (Virtual) Equipments [arXiv:1612.02762]
-
David Jaz Myers, String Diagrams for (Virtual) Proarrow Equipments (2017) [slides: pdf, pdf]
See also at opetopic type theory.
Discussion of sheet diagrams for rig categories is in
- Cole Comfort, Antonin Delpeuch, Jules Hedges, Sheet diagrams for bimonoidal categories, (arXiv:2010.13361)
Discussion of the use of string diagrams to treat universal constructions such as limits, Kan extensions, and ends:
- Kenji Nakahira, Diagrammatic category theory [arXiv:2307.08891]
A book on higher-categorical diagrams:
- Amar Hadzihasanovic, Combinatorics of higher-categorical diagrams [arXiv:2404.07273]
Software
The higher dimensional string diagrams (“zoom complexes” (Kock-Joyal-Batanin-Mascari 07)) used for presenting opetopes in the context of opetopic type theory are introduced in
-
Eric Finster, Opetopic Diagrams 1 - Basics (video)
-
Eric Finster, Opetopic Diagrams 2 - Geometry (video)
-
Globular is a web-based proof assistant for finitely-presented semistrict globular higher categories. It allows one to formalize higher-categorical proofs in finitely-presented n-categories and visualize them as string diagrams.
Quantum information theory via String diagrams
General
The observation that a natural language for quantum information theory and quantum computation, specifically for quantum circuit diagrams, is that of string diagrams in †-compact categories (see quantum information theory via dagger-compact categories):
-
Samson Abramsky, Bob Coecke, A categorical semantics of quantum protocols, Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press (2004) arXiv:quant-ph/0402130, doi:10.1109/LICS.2004.1319636
-
Samson Abramsky, Bob Coecke, Abstract Physical Traces, Theory and Applications of Categories, 14 6 (2005) 111-124. [tac:14-06, arXiv:0910.3144]
-
Samson Abramsky, Bob Coecke, Categorical quantum mechanics, in Handbook of Quantum Logic and Quantum Structures, Elsevier (2008) arXiv:0808.1023, ISBN:9780080931661, doi:10.1109/LICS.2004.1319636
-
Bob Coecke, De-linearizing Linearity: Projective Quantum Axiomatics from Strong Compact Closure, Proceedings of the 3rd International Workshop on Quantum Programming Languages (2005), Electronic Notes in Theoretical Computer Science 170 (2007) 49-72 [doi:10.1016/j.entcs.2006.12.011, arXiv:quant-ph/0506134]
On the relation to quantum logic/linear logic:
-
Samson Abramsky, Ross Duncan, A Categorical Quantum Logic, Mathematical Structures in Computer Science 16 3 (2006) arXiv:quant-ph/0512114, doi:10.1017/S0960129506005275
-
Ross Duncan, Types for quantum mechanics, 2006 pdf, slides
Early exposition with introduction to monoidal category theory:
-
Bob Coecke, Kindergarten quantum mechanics arXiv:quant-ph/0510032
-
Bob Coecke, Introducing categories to the practicing physicist arXiv:0808.1032
-
John Baez, Mike Stay, Physics, topology, logic and computation: a rosetta stone in: New Structures for Physics, Bob Coecke (ed.), Lecture Notes in Physics 813, Springer (2011) 95-174 arxiv/0903.0340
-
Bob Coecke, Eric Oliver Paquette, Categories for the practising physicist, in: New Structures for Physics, Lecture Notes in Physics 813, Springer (2010) arXiv:0905.3010, doi:10.1007/978-3-642-12821-9_3
-
Bob Coecke, Quantum Picturalism, Contemporary Physics 51 1 (2010) arXiv:0908.1787, doi:10.1080/00107510903257624
Review in contrast to quantum logic:
- Samson Abramsky, Bob Coecke, Physics from Computer Science: a Position Statement, International Journal of Unconventional Computing 3 3 (2007) pdf, ijuc-3-3-p-179-197
and with emphasis on quantum computation:
- Jamie Vicary, The Topology of Quantum Algorithms, (LICS 2013) Proceedings of 28th Annual ACM/IEEE Symposium on Logic in Computer Science (2013) 93-102 arXiv:1209.3917, doi:10.1109/LICS.2013.14
Generalization to quantum operations on mixed states (completely positive maps of density matrices):
-
Peter Selinger, Dagger compact closed categories and completely positive maps, Electronic Notes in Theoretical Computer Science 170 (2007) 139-163 doi:10.1016/j.entcs.2006.12.018, web, pdf
-
Bob Coecke, Chris Heunen, Pictures of complete positivity in arbitrary dimension, Information and Computation 250 50-58 (2016) arXiv:1110.3055, doi:10.1016/j.ic.2016.02.007
-
Bob Coecke, Chris Heunen, Aleks Kissinger,
Categories of Quantum and Classical Channels, EPTCS 158 (2014) 1-14 arXiv:1408.0049, doi:10.4204/EPTCS.158.1
Textbook accounts (with background on relevant monoidal category theory):
-
Bob Coecke, Aleks Kissinger, Picturing Quantum Processes – A First Course in Quantum Theory and Diagrammatic Reasoning, Cambridge University Press (2017) ISBN:9781107104228
-
Chris Heunen, Jamie Vicary: Categories for Quantum Theory, Oxford University Press (2019) [ISBN:9780198739616]
based on:
Chris Heunen, Jamie Vicary, Lectures on categorical quantum mechanics (2012) [pdf, pdf]
-
Bob Coecke, Stefano Gogioso, Quantum in Pictures, Quantinuum Publications (2023) ISBN 978-1739214715, Quantinuum blog
(focus on ZX-calculus)
Measurement & Classical structures
Formalization of quantum measurement via Frobenius algebra-structures (“classical structures”):
-
Bob Coecke, Duško Pavlović, Quantum measurements without sums, in Louis Kauffman, Samuel Lomonaco (eds.), Mathematics of Quantum Computation and Quantum Technology, Taylor & Francis (2008) 559-596 arXiv:quant-ph/0608035, doi:10.1201/9781584889007
-
Bob Coecke, Eric Oliver Paquette, POVMs and Naimark’s theorem without sums, Electronic Notes in Theoretical Computer Science 210 (2008) 15-31 arXiv:quant-ph/0608072, doi:10.1016/j.entcs.2008.04.015
-
Bob Coecke, Eric Oliver Paquette, Duško Pavlović, Classical and quantum structuralism, in: Semantic Techniques in Quantum Computation, Cambridge University Press (2009) 29-69 arXiv:0904.1997, doi:10.1017/CBO9781139193313.003
-
Bob Coecke, Duško Pavlović, Jamie Vicary, A new description of orthogonal bases, Mathematical Structures in Computer Science 23 3 (2012) 555- 567 arXiv:0810.0812, doi:10.1017/S0960129512000047
and the evolution of the “classical structures”-monad into the “spider”-diagrams (terminology for special Frobenius normal form, originating in Coecke & Paquette 2008, p. 6, Coecke & Duncan 2008, Thm. 1) of the ZX-calculus:
-
Bob Coecke, Ross Duncan, §3 in: Interacting Quantum Observables, in Automata, Languages and Programming. ICALP 2008, Lecture Notes in Computer Science 5126, Springer (2008) doi:10.1007/978-3-540-70583-3_25
-
Aleks Kissinger, §§2 in: Graph Rewrite Systems for Classical Structures in -Symmetric Monoidal Categories, MSc thesis, Oxford (2008) pdf, pdf
-
Aleks Kissinger, §4 in: Exploring a Quantum Theory with Graph Rewriting and Computer Algebra, in: Intelligent Computer Mathematics. CICM 2009, Lecture Notes in Computer Science 5625 (2009) 90-105 doi:10.1007/978-3-642-02614-0_12
-
Bob Coecke, Ross Duncan, Def. 6.4 in: Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 arXiv:0906.4725, doi:10.1088/1367-2630/13/4/043016
ZX-Calculus
Evolution of the “classical structures”-Frobenius algebra (above) into the “spider”-ingredient of the ZX-calculus for specific control of quantum circuit-diagrams:
-
Bob Coecke, Ross Duncan, §3 in: Interacting Quantum Observables, in Automata, Languages and Programming. ICALP 2008, Lecture Notes in Computer Science 5126, Springer (2008) doi:10.1007/978-3-540-70583-3_25
-
Aleks Kissinger, Graph Rewrite Systems for Classical Structures in -Symmetric Monoidal Categories, MSc thesis, Oxford (2008) pdf, pdf
-
Aleks Kissinger, Exploring a Quantum Theory with Graph Rewriting and Computer Algebra, in: Intelligent Computer Mathematics. CICM 2009, Lecture Notes in Computer Science 5625 (2009) 90-105 doi:10.1007/978-3-642-02614-0_12
-
Bob Coecke, Ross Duncan, Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 arXiv:0906.4725, doi:10.1088/1367-2630/13/4/043016
Relating the ZX-calculus to braided fusion categories for anyon braiding:
- Fatimah Rita Ahmadi, Aleks Kissinger, Topological Quantum Computation Through the Lens of Categorical Quantum Mechanics arXiv:2211.03855
Last revised on August 23, 2025 at 08:29:48. See the history of this page for a list of all contributions to it.