nLab equivariant cell structure on 2-tori -- section
Equivariant cell structure on 2-tori
The following shows for the 2D crystallographic groups (wallpaper groups)
the -CW complex structure on the resulting G-tori (graphics from SS25).
The point groups arising are the cyclic groups , , , , and the dihedral groups , , , , and (making 9 distinct abstract point groups , due to the isomorphism , but several come with distinct group actions on ).
| wallpaper group | point group | G-cell structure on |
|---|---|---|
| p1 | Ex. | |
| pm | Ex. | |
| cm | Ex. | |
| pg | Ex. | |
| p2 | Ex. | |
| pmm | Ex. | |
| cmm | Ex. | |
| pmg | Ex. | |
| pgg | Ex. | |
| p3 | Ex. | |
| p31m | Ex. | |
| p3m1 | Ex. | |
| p4 | Ex. | |
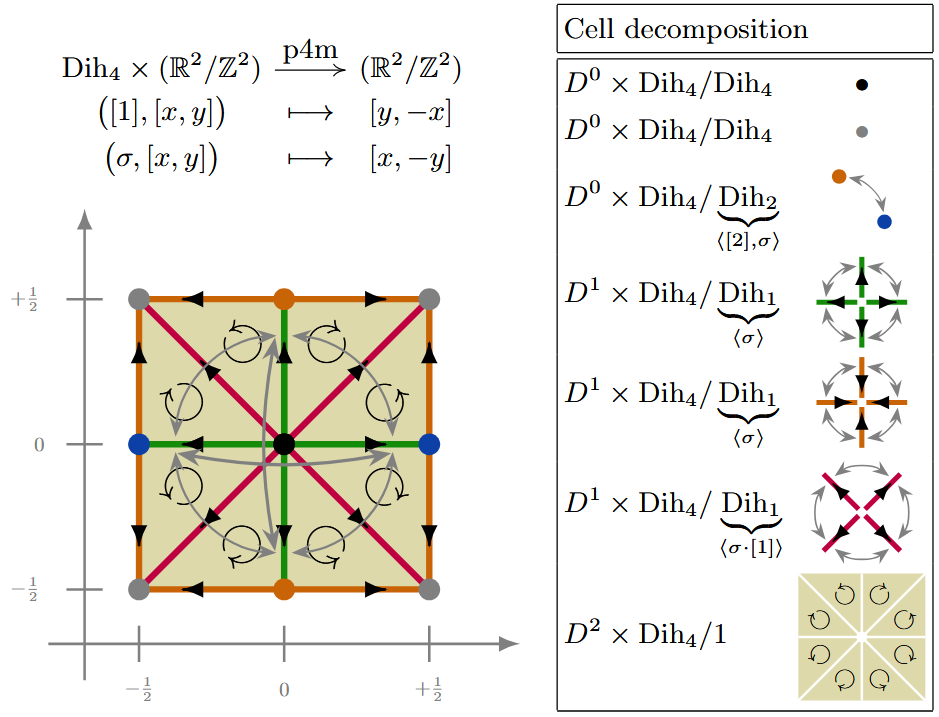
| p4m | Ex. | |
| p4g | Ex. | |
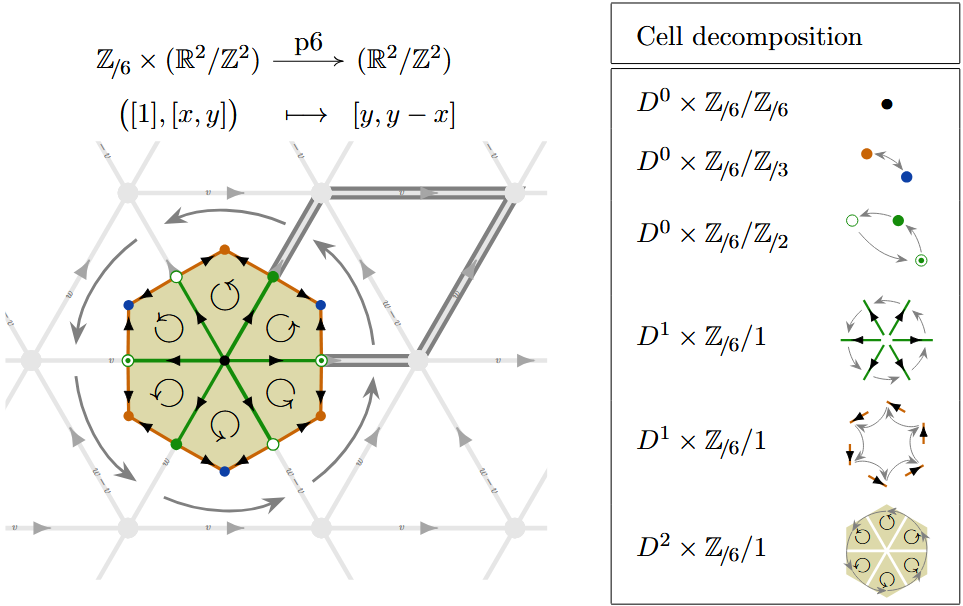
| p6 | Ex. | |
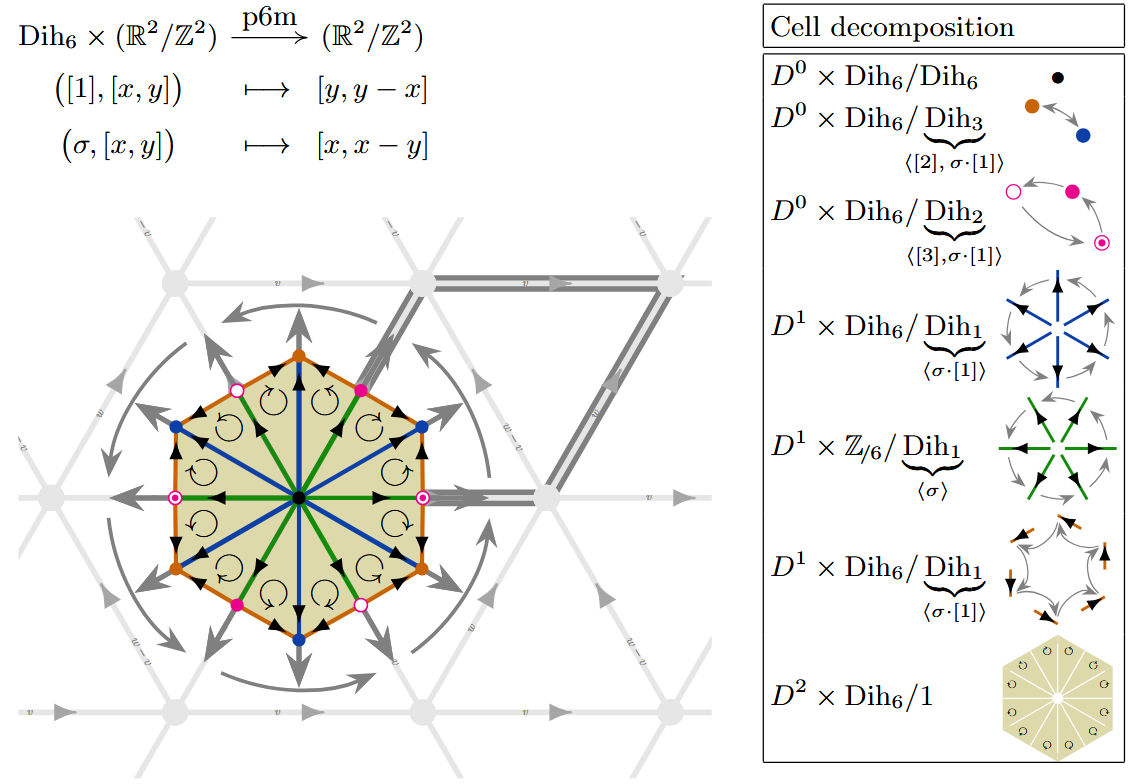
| p6m | Ex. |
Example
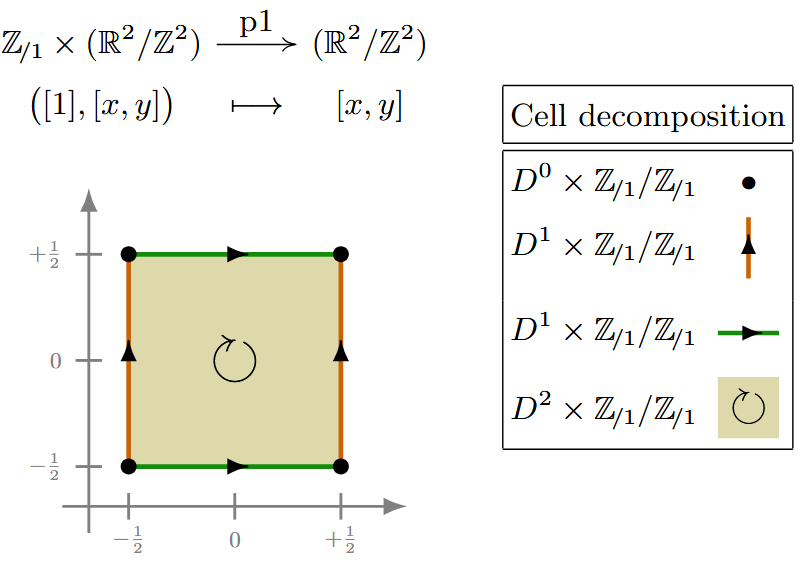
(p1) For completeness, here is a -CW complex structure for the torus equipped with trivial group-action, corresponding to the wallpaper group:
Example
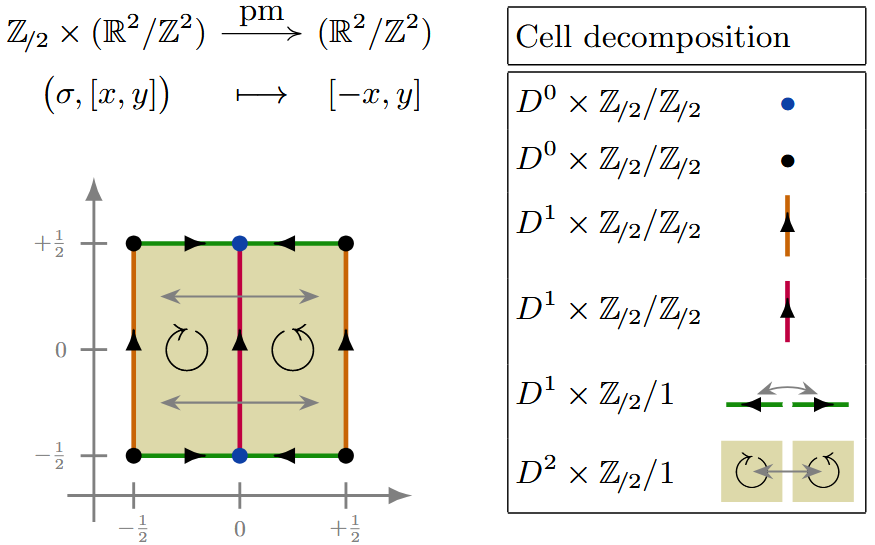
(pm) Here is a -CW complex structure for the torus equipped with the -action which reflects one of the two coordinate axes, corresponding to the wallpaper group:
Example
(cm) Here is a -CW complex structure for the torus equipped with the -action which reflects along the coordinate diagonal, corresponding to the wallpaper group:
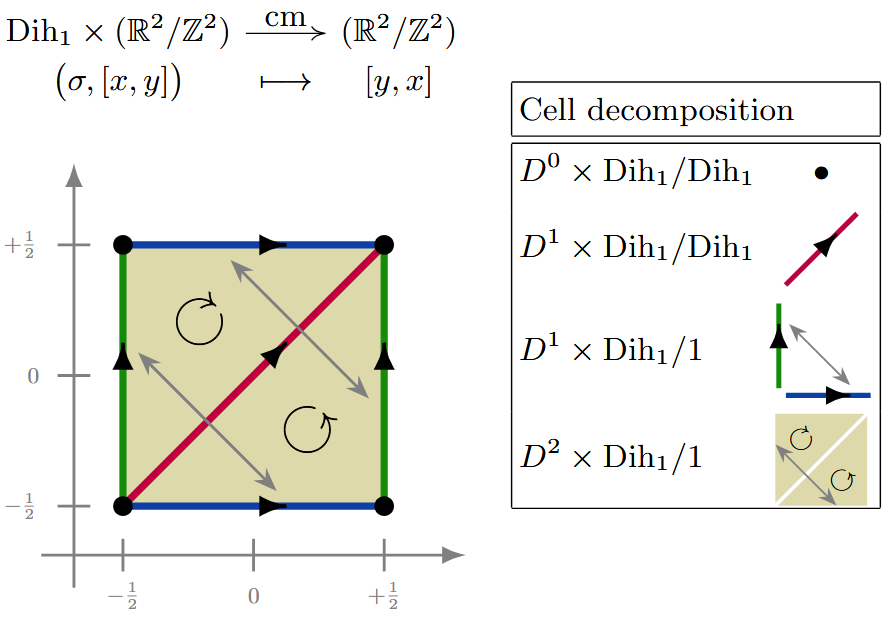
Example
(pg) Here is a -CW complex structure for the torus equipped with glide reflection action corresponding to the wallpaper group :
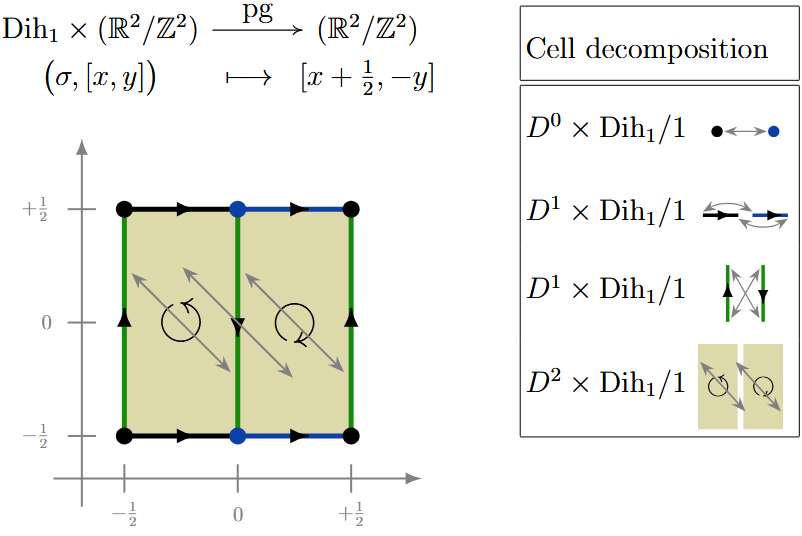
Example
(p2) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin, corresponding to the wallpaper group :
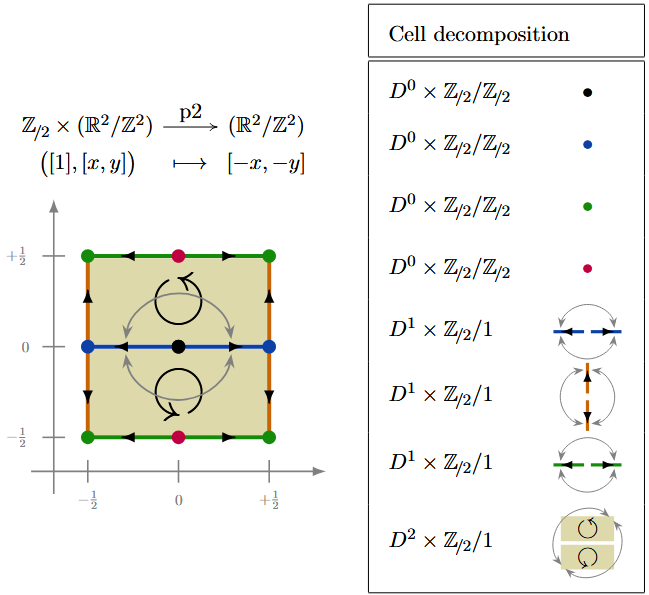
Example
(pmm) Here is a -CW complex structure for the torus equipped with -action according to the wallpaper group pmm:
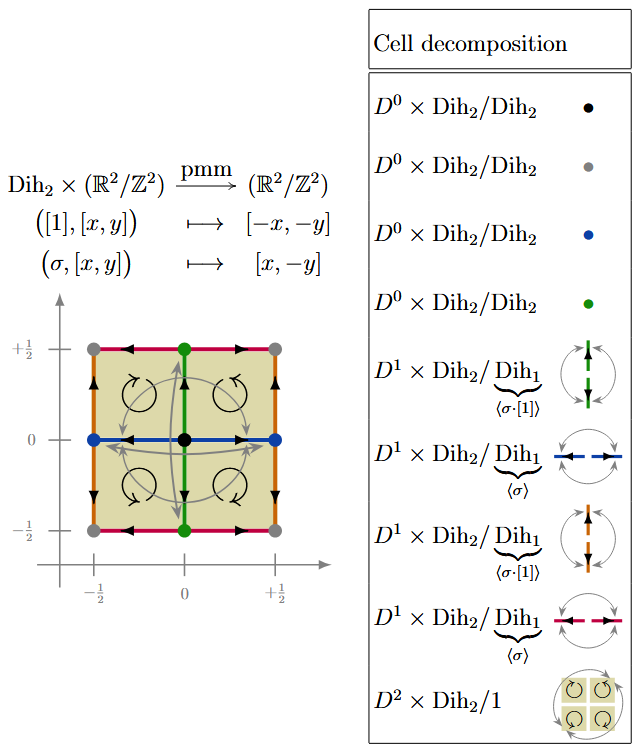
Example
(cmm) Here is a -CW complex structure for the torus equipped with -action according to the wallpaper group cmm:
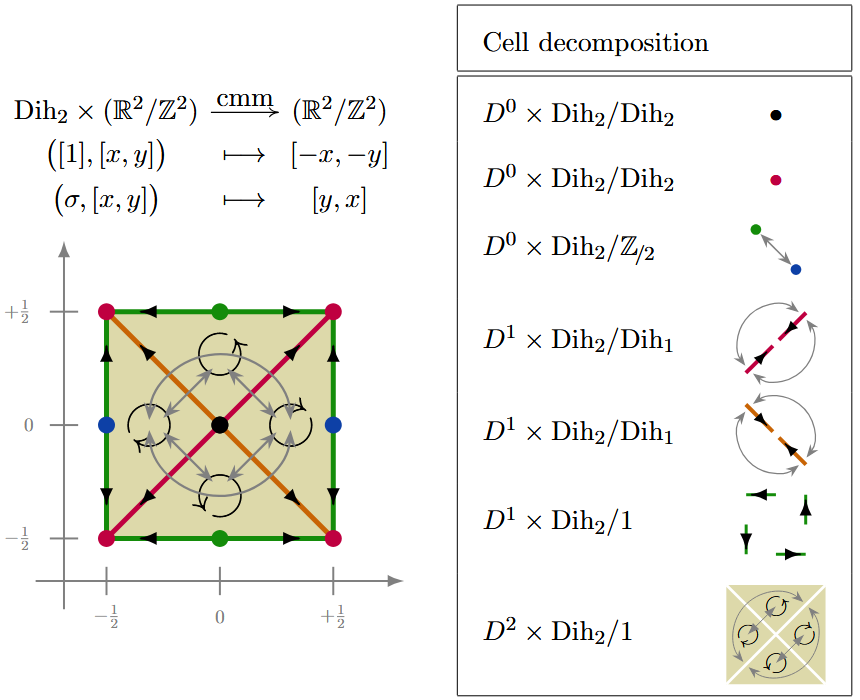
Example
(pmg) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
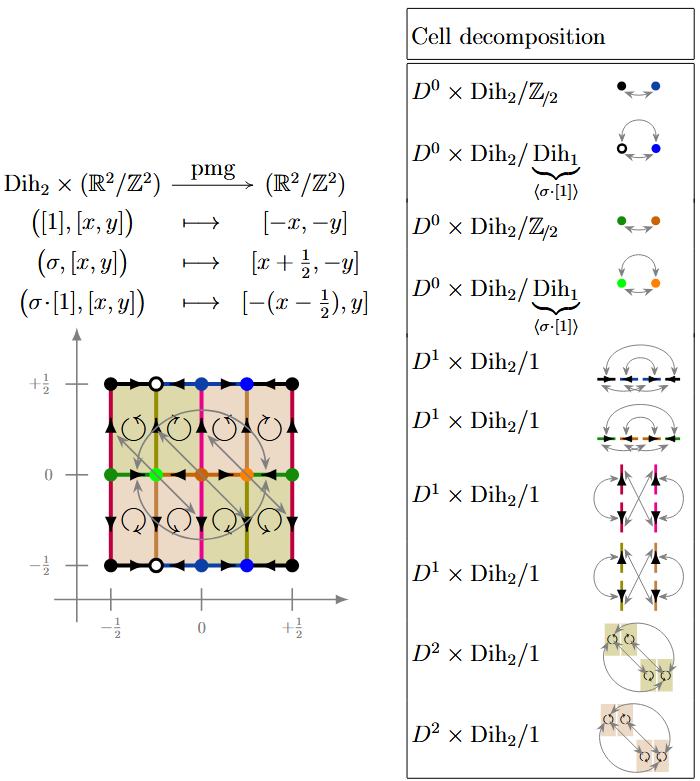
Example
(pgg) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
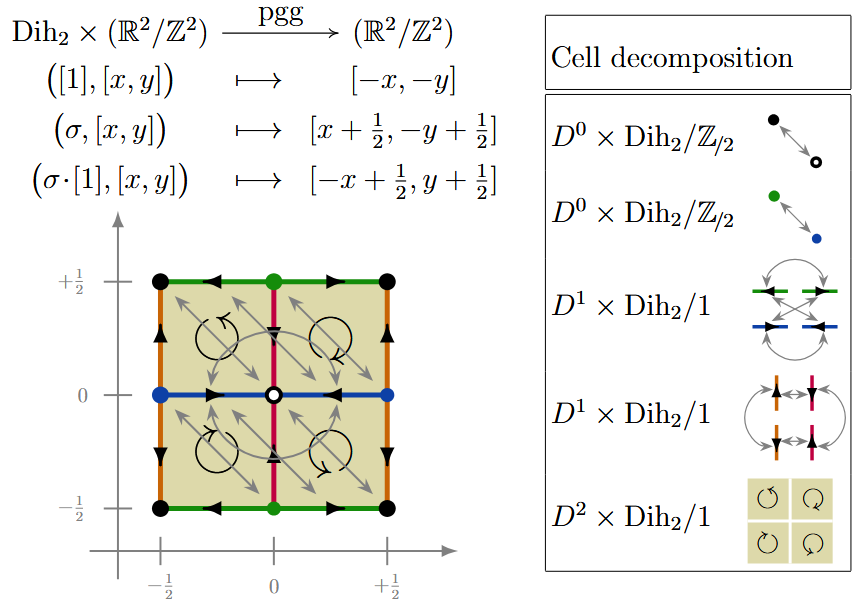
Example
(p3) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
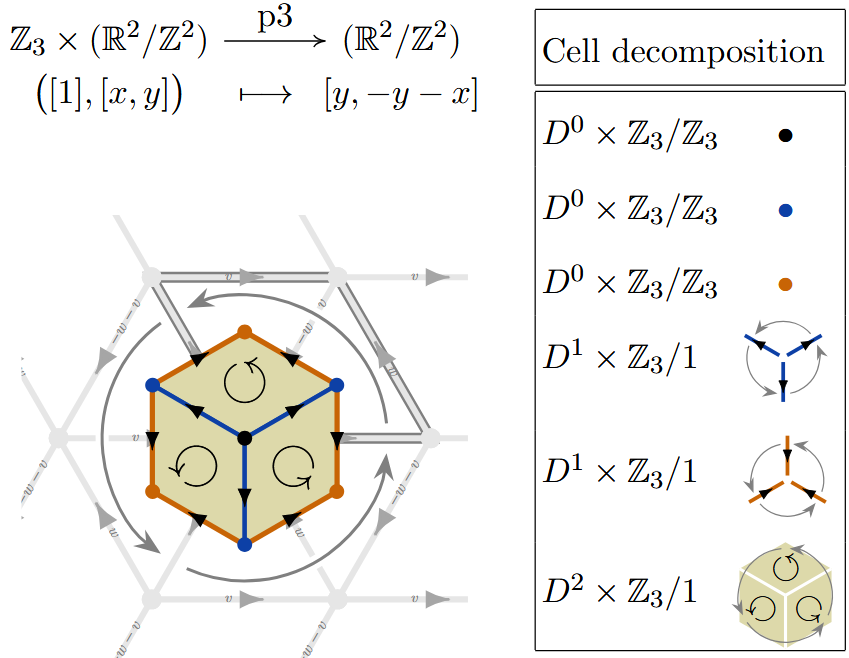
Example
(p31m) Here is a -CW complex structure for the torus equipped with -action corresponding to the wallpaper group:
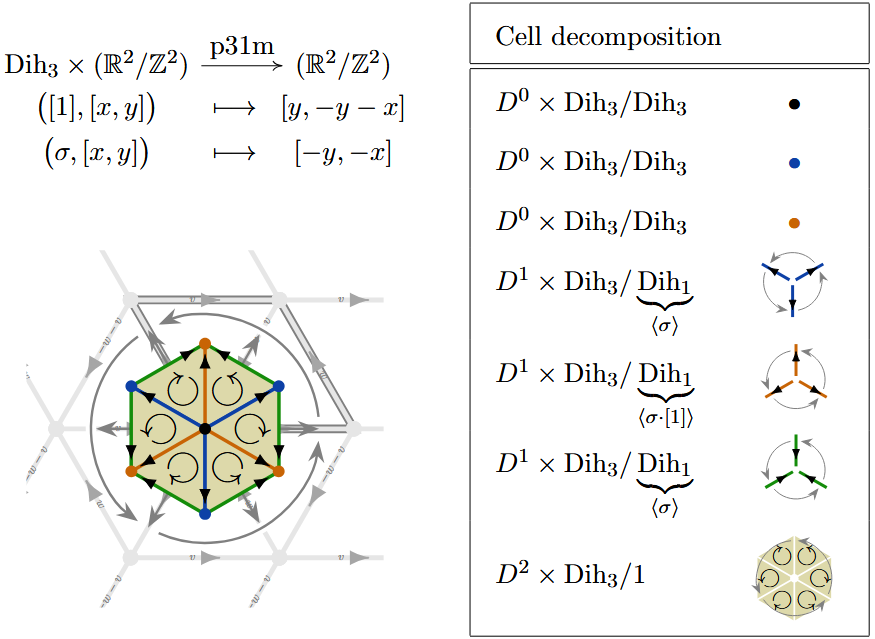
Example
(p3m1) Here is a -CW complex structure for the torus equipped with the -action corresponding to the wallpaper group:
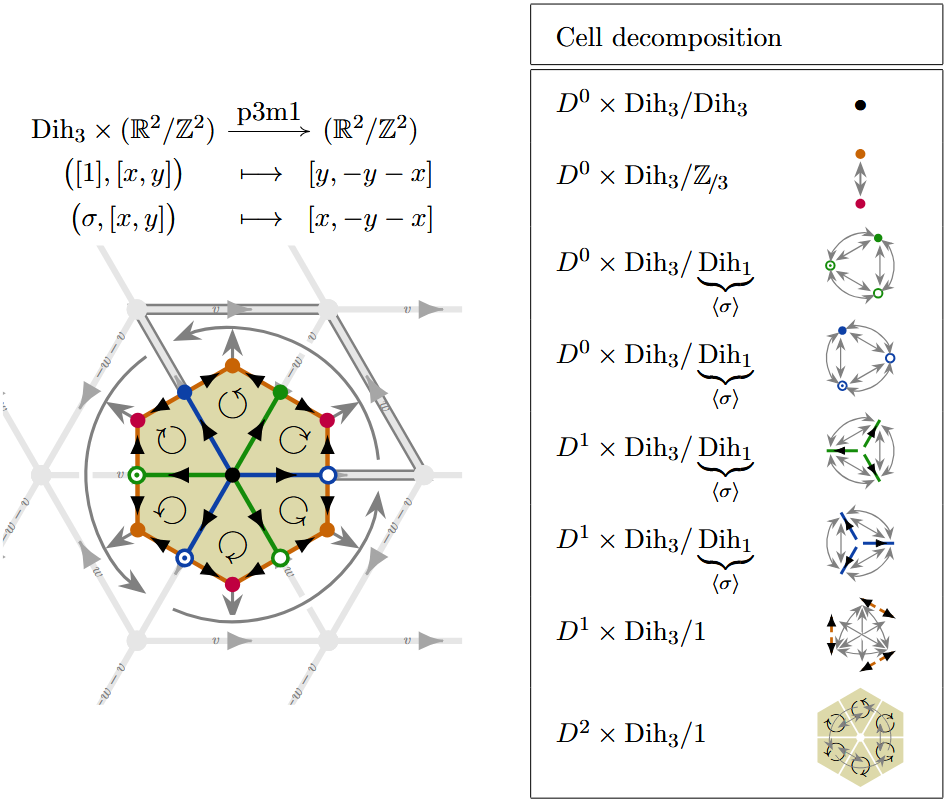
Example
(p4) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
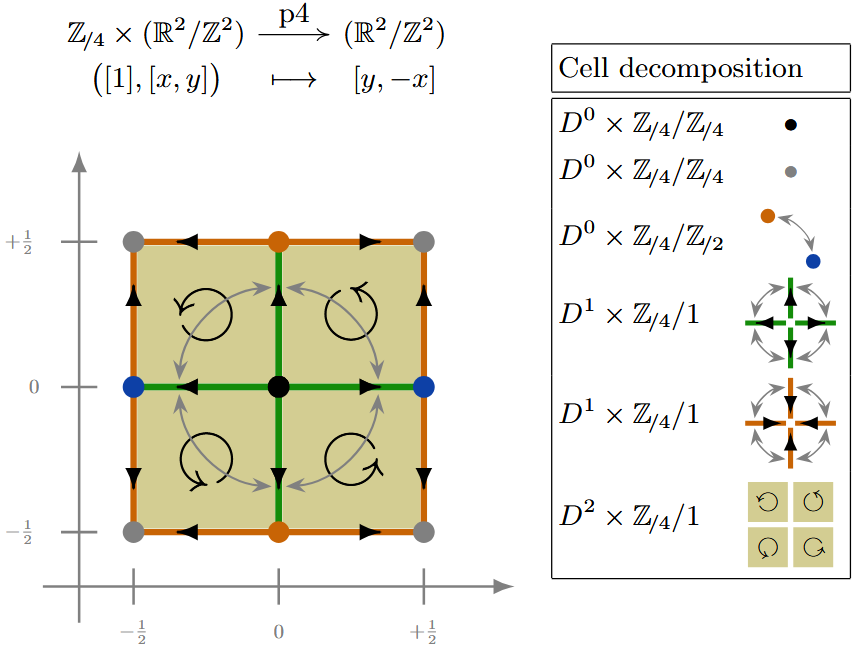
Example
(p4g) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
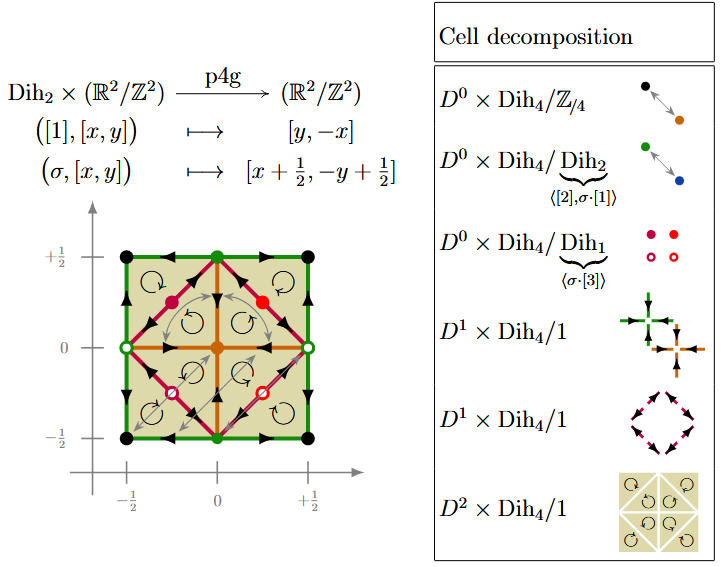
Example
(p6) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
Last revised on August 30, 2025 at 19:49:55. See the history of this page for a list of all contributions to it.