nLab torus
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Contents
Definition
In topology and differential geometry
The torus is the manifold (a smooth manifold, hence in particular also a topological manifold) obtained as the quotient
of the Cartesian plane, regarded as an abelian group, by the subgroup of pairs of integers.
As a topological space this is the quotient topological space obtained from the square by identifying opposite sides:
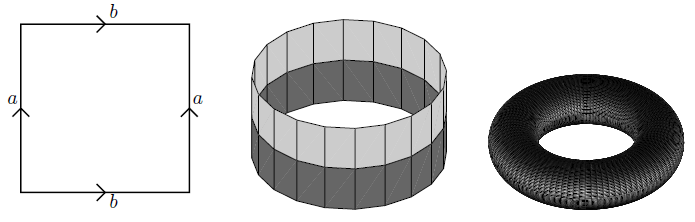
graphics grabbed from Lawson 03
More generally, for any natural number, the -torus is
For this is the circle.
In this fashion each torus canonically carries the structure of an abelian group, in fact of an abelian Lie group. Notice that regarded as a group the torus carries a base point (the neutral element).
In algebraic geometry
According to SGA3, for a base scheme then a 1-dimensional torus (in the sense of tori-as-groups) over it is a group scheme over which becomes isomorphic to the multiplicative group over after a faithfully flat group extension.
In (Lawson-Naumann 12, def. A.1) this is called “a form of” the multiplicative group over .
By (Lawson-Naumann 12, prop. A.4) the moduli stack of 1-dimensional tori in this sense is equivalent to the delooping of the group of order two:
The single nontrival automorphism of any 1-dimensional toris here is that induced by the canonical automorphism of the multiplicative group
which is the inversion involution (given by sending any element to its inverse element).
As a homotopy type
As a homotopy type the torus is the product of two copies of the circle.
In homotopy type theory the torus can be formalized as the higher inductive type generated by a point base, two paths, and , from base to itself, and an element of . It has been formally shown (Sojakova15) that this type is equivalent to the product of two circles. For a treatment in cubical type theory, see (Licata-Brunierie).
The stable homotopy type of the torus is the wedge sum of 2 circles and one 2-sphere (eg. Freed & Moore 13, Thm. 11.8):
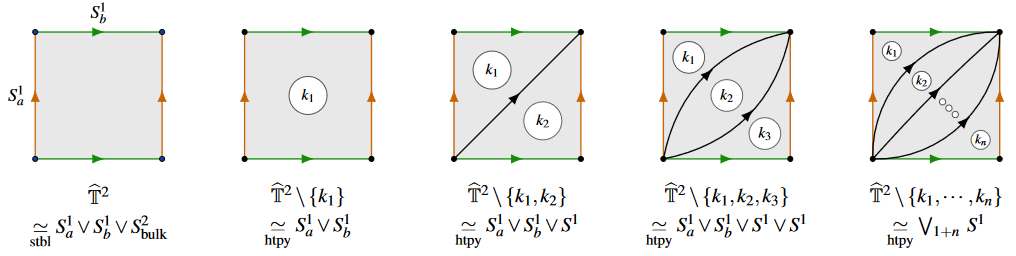 (graphics from SS 22)
(graphics from SS 22)
Properties
- The character group of a torus is isomorphic to its fundamental group, which is . See also at Pontryagin duality and at moduli space of flat connections.
Related concepts
References
- Terry Lawson, Topology: A Geometric Approach, Oxford University Press (2003) (pdf)
On the ordinary cohomology of topological tori:
The moduli stack of 1-dimensional tori in algebraic geometry is discussed (as the cusp point inside the moduli stack of elliptic curves) in
- Tyler Lawson, Niko Naumann, Appendix A of Strictly commutative realizations of diagrams over the Steenrod algebra and topological modular forms at the prime 2 (arXiv:1203.1696)
Discussion of tori the homotopy type of the torus in homotopy type theory is in
-
Kristina Sojakova, The equivalence of the torus and the product of two circles in homotopy type theory, (arXiv:1510.03918)
-
Dan Licata, Guillaume Brunerie, A cubical approach to synthetic homotopy theory (pdf)
On 2-group-extensions of torus groups:
- Nora Ganter, Categorical Tori, SIGMA 14 (2018), 014, 18 (arXiv:1406.7046)
On the stable homotopy type of the torus:
- Daniel Freed, Gregory Moore, Thm. 11.8 of: Twisted equivariant matter, Ann. Henri Poincaré (2013) 14: 1927 (arXiv:1208.5055)
On topological complexity of tori (or more general products of spheres)
- Michael Farber, Topological complexity of motion planning (2001), arXiv:math/0111197;
Last revised on February 14, 2024 at 06:40:14. See the history of this page for a list of all contributions to it.