nLab wallpaper group
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Contents
Definition
A wallpaper group is a crystallographic group (space group) in dimension 2, hence a subgroup of the isometry group of the Euclidean plane such that
-
the part of inside the translation group is generated by two linearly independent vectors;
-
the point group is finite.
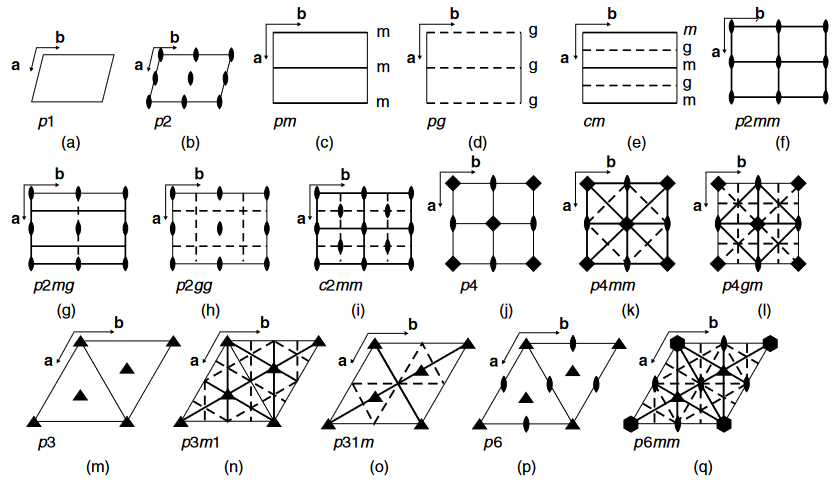
Tabulation
Crystallographic diagrams
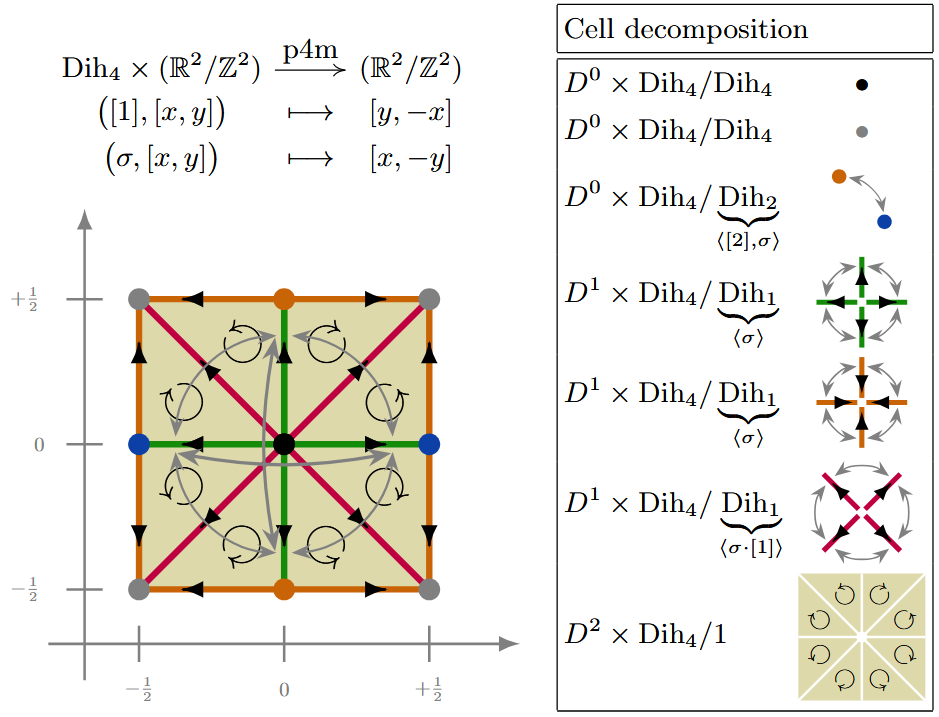
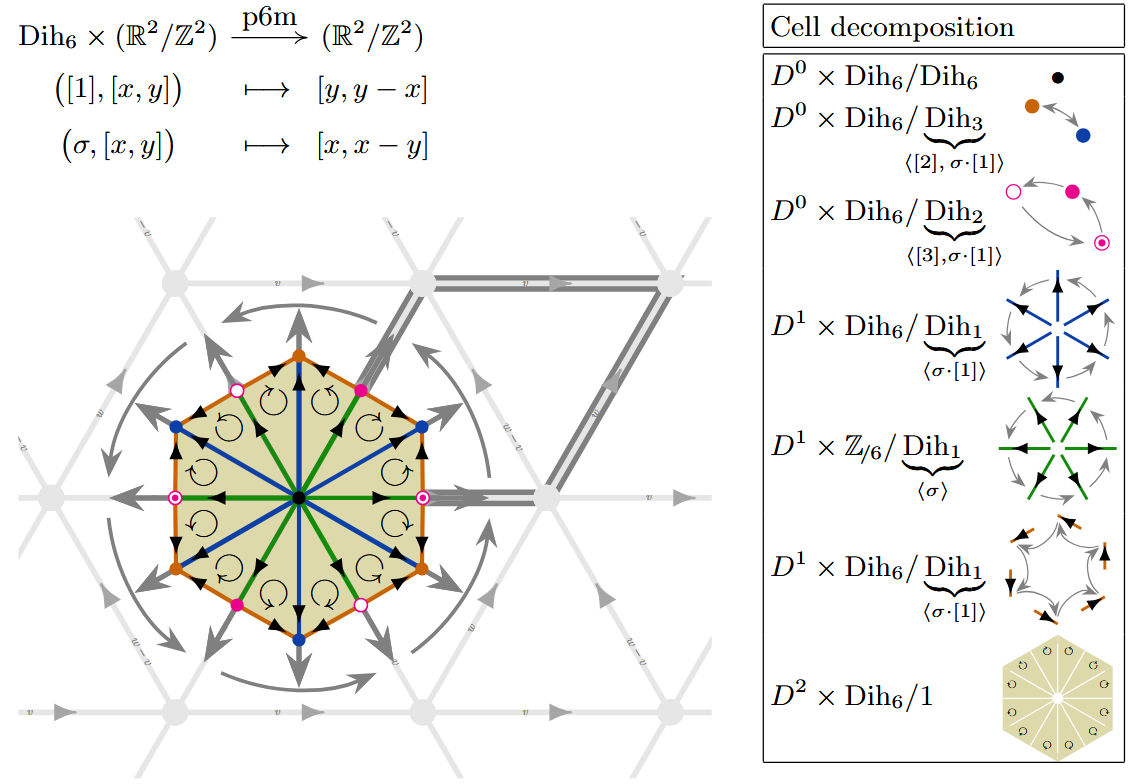
Equivariant cell structure on 2-tori
The following shows for the 2D crystallographic groups (wallpaper groups)
the -CW complex structure on the resulting G-tori (graphics from SS25).
The point groups arising are the cyclic groups , , , , and the dihedral groups , , , , and (making 9 distinct abstract point groups , due to the isomorphism , but several come with distinct group actions on ).
| wallpaper group | point group | G-cell structure on |
|---|---|---|
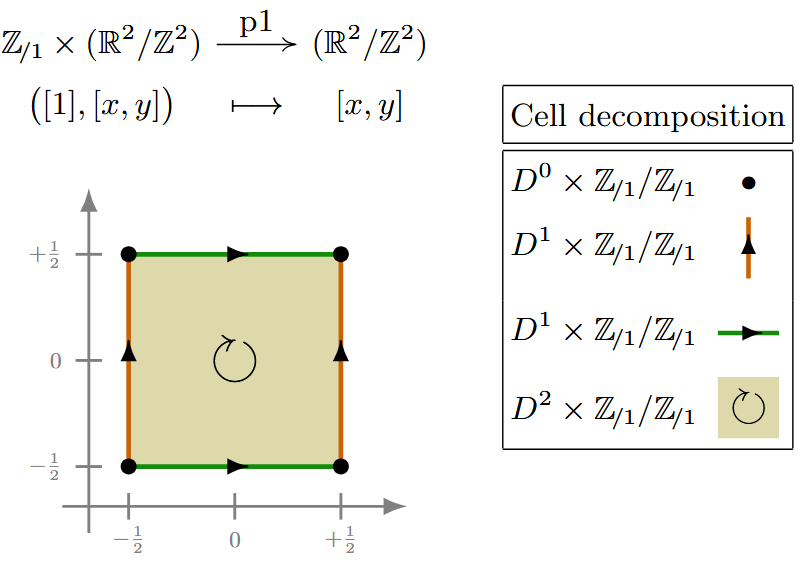
| p1 | Ex. | |
| pm | Ex. | |
| cm | Ex. | |
| pg | Ex. | |
| p2 | Ex. | |
| pmm | Ex. | |
| cmm | Ex. | |
| pmg | Ex. | |
| pgg | Ex. | |
| p3 | Ex. | |
| p31m | Ex. | |
| p3m1 | Ex. | |
| p4 | Ex. | |
| p4m | Ex. | |
| p4g | Ex. | |
| p6 | Ex. | |
| p6m | Ex. |
Example
(p1) For completeness, here is a -CW complex structure for the torus equipped with trivial group-action, corresponding to the wallpaper group:
Example
(pm) Here is a -CW complex structure for the torus equipped with the -action which reflects one of the two coordinate axes, corresponding to the wallpaper group:
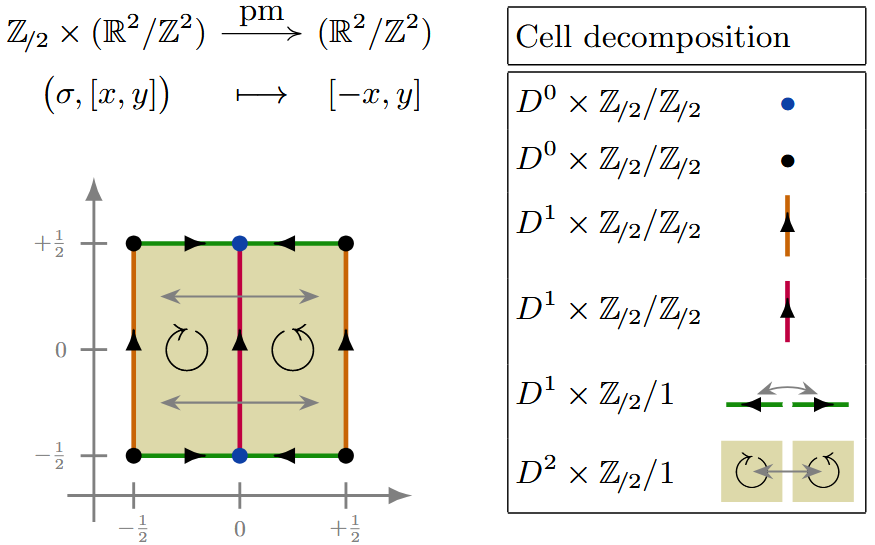
Example
(cm) Here is a -CW complex structure for the torus equipped with the -action which reflects along the coordinate diagonal, corresponding to the wallpaper group:
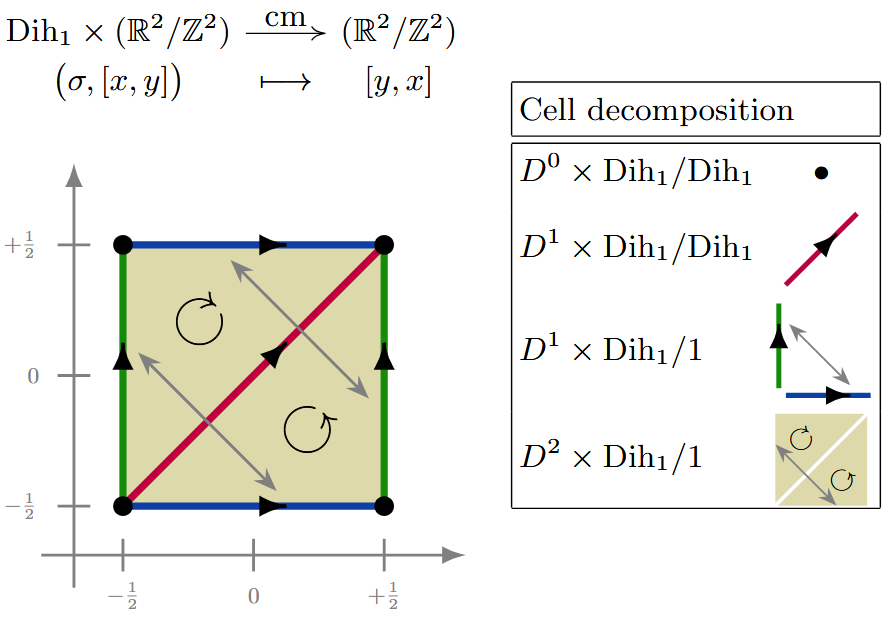
Example
(pg) Here is a -CW complex structure for the torus equipped with glide reflection action corresponding to the wallpaper group :
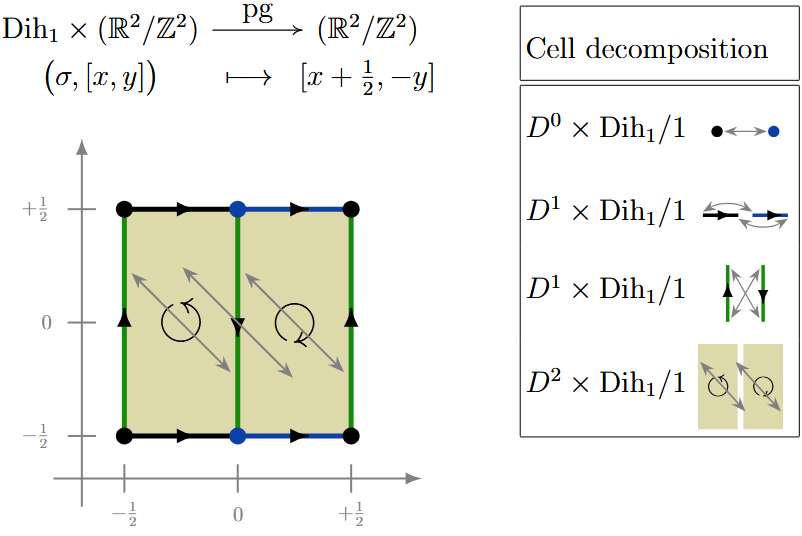
Example
(p2) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin, corresponding to the wallpaper group :
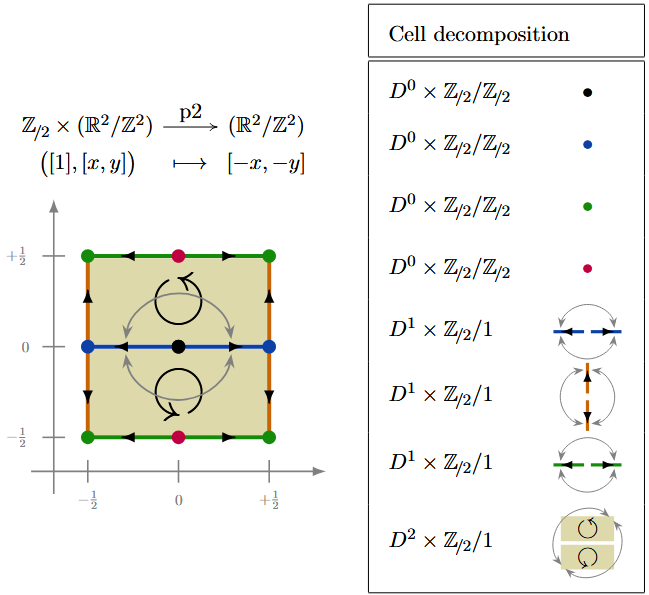
Example
(pmm) Here is a -CW complex structure for the torus equipped with -action according to the wallpaper group pmm:
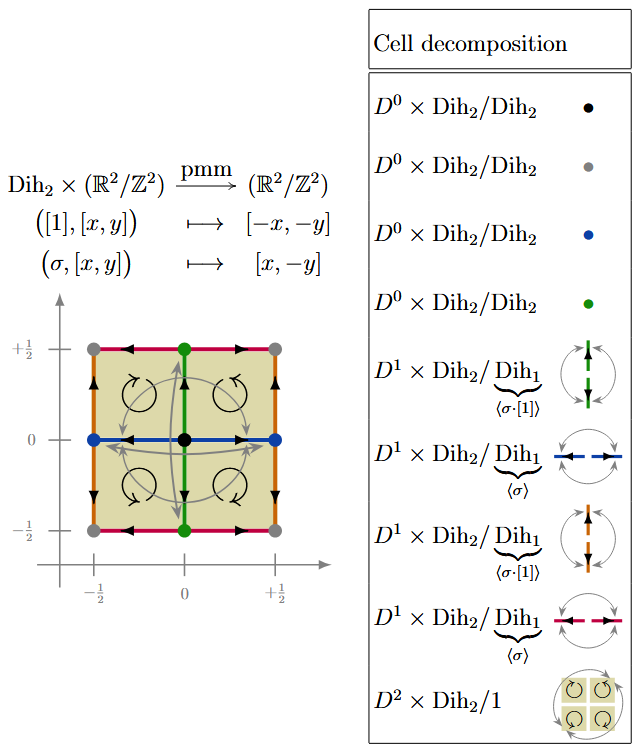
Example
(cmm) Here is a -CW complex structure for the torus equipped with -action according to the wallpaper group cmm:
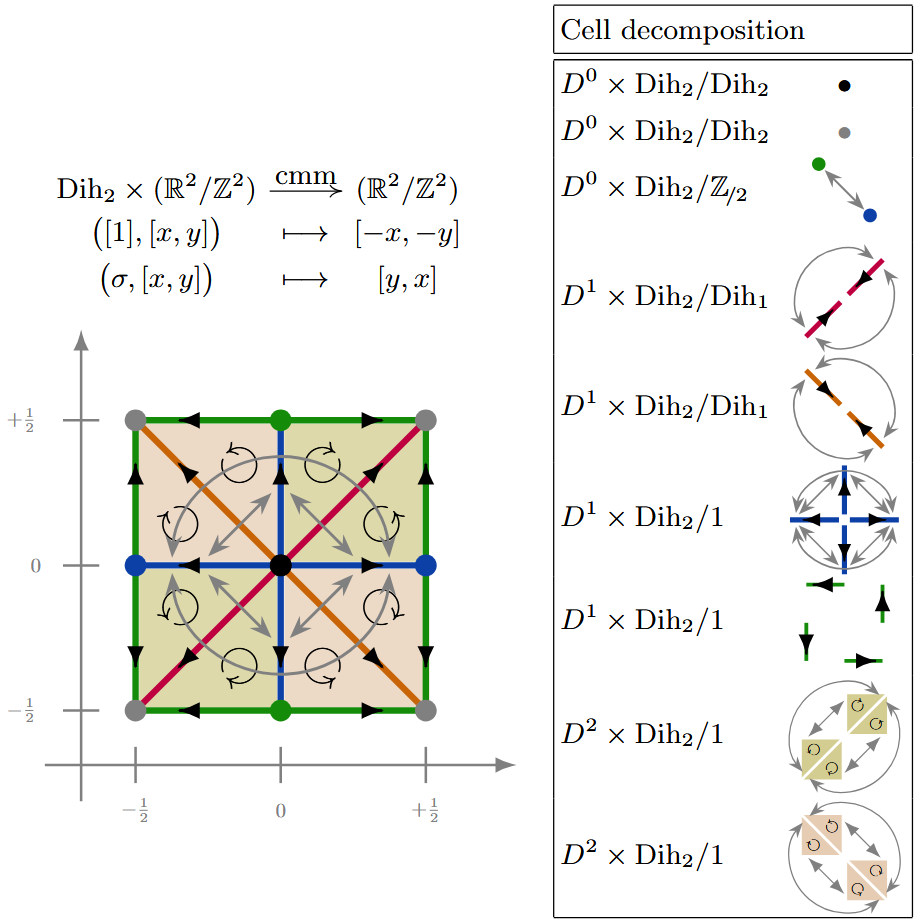
Example
(pmg) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
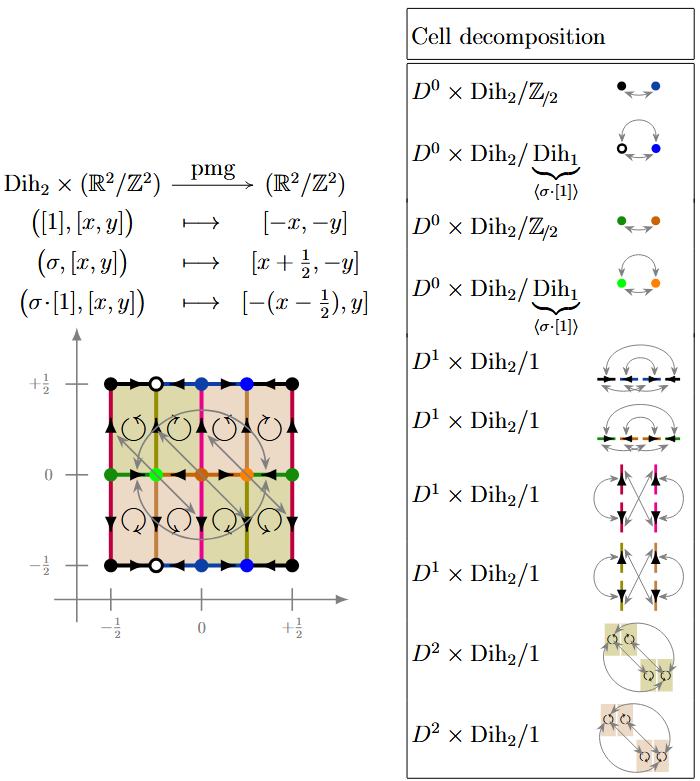
Example
(pgg) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
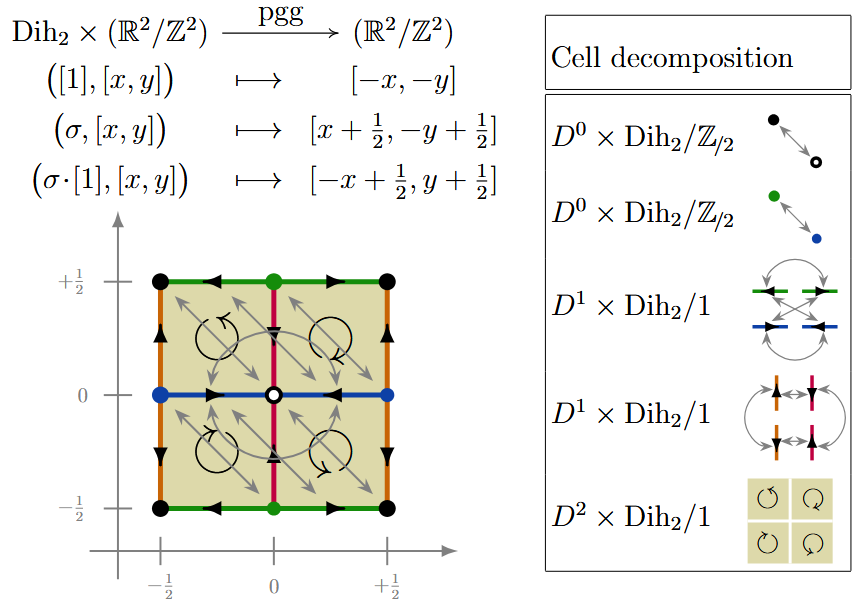
Example
(p3) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
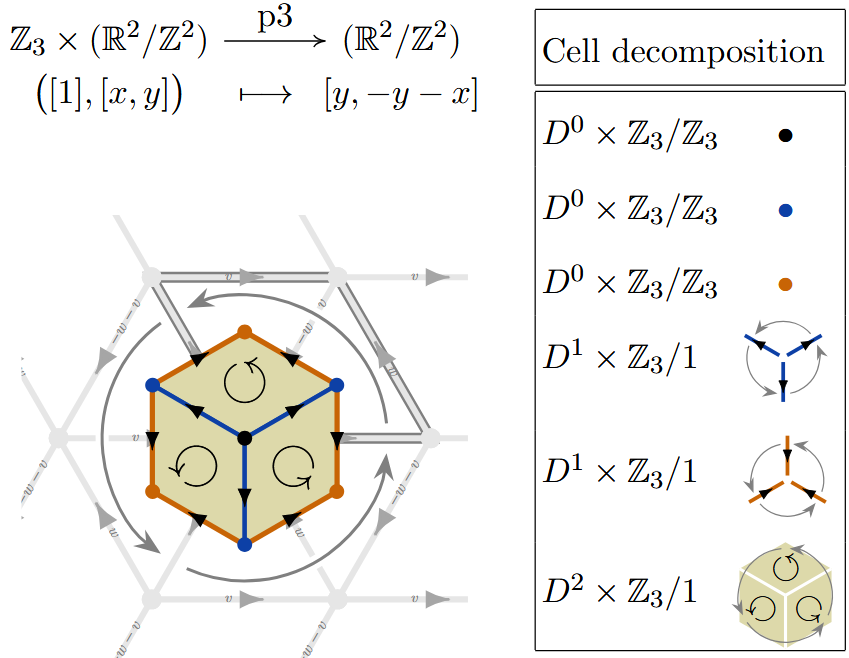
Example
(p31m) Here is a -CW complex structure for the torus equipped with -action corresponding to the wallpaper group:
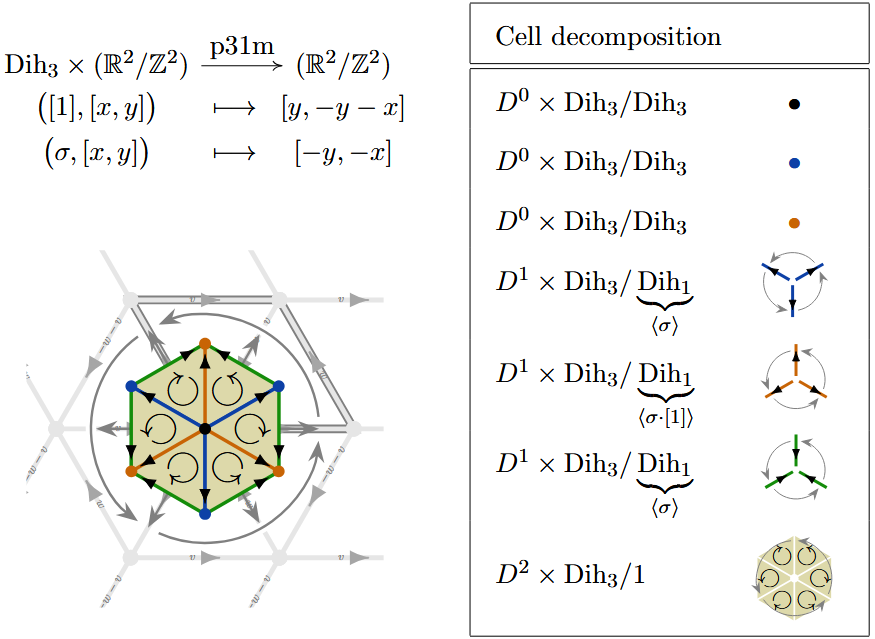
Example
(p3m1) Here is a -CW complex structure for the torus equipped with the -action corresponding to the wallpaper group:
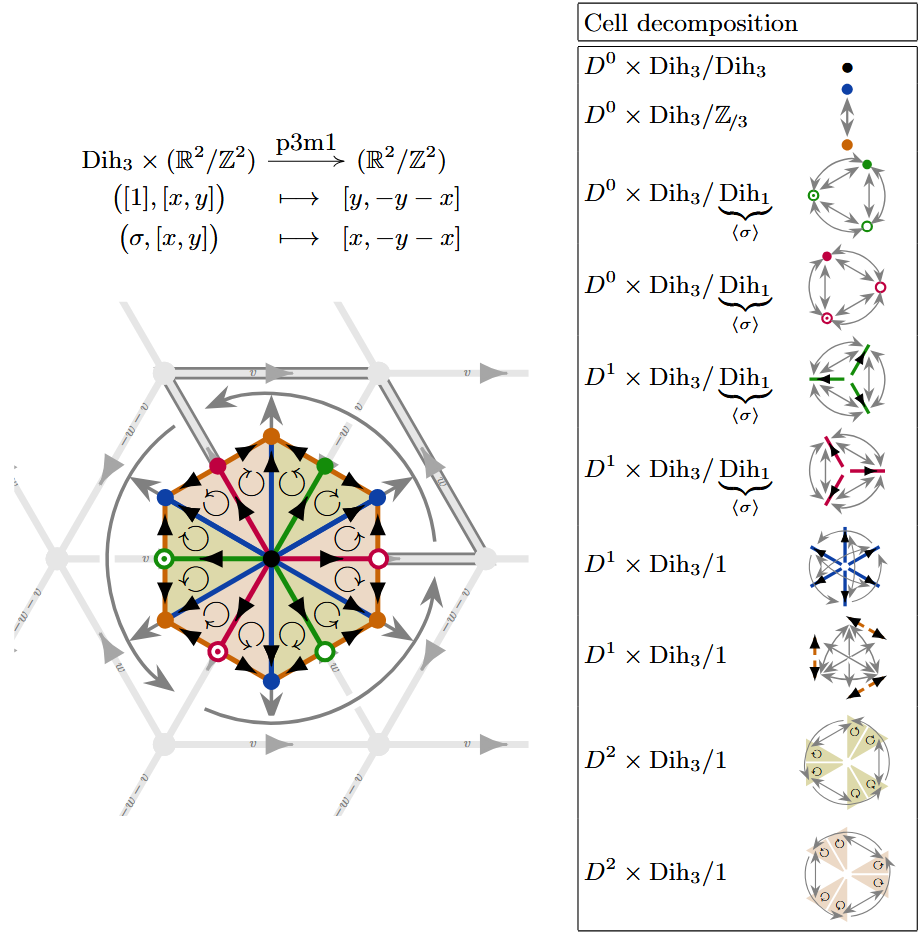
Example
(p4) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
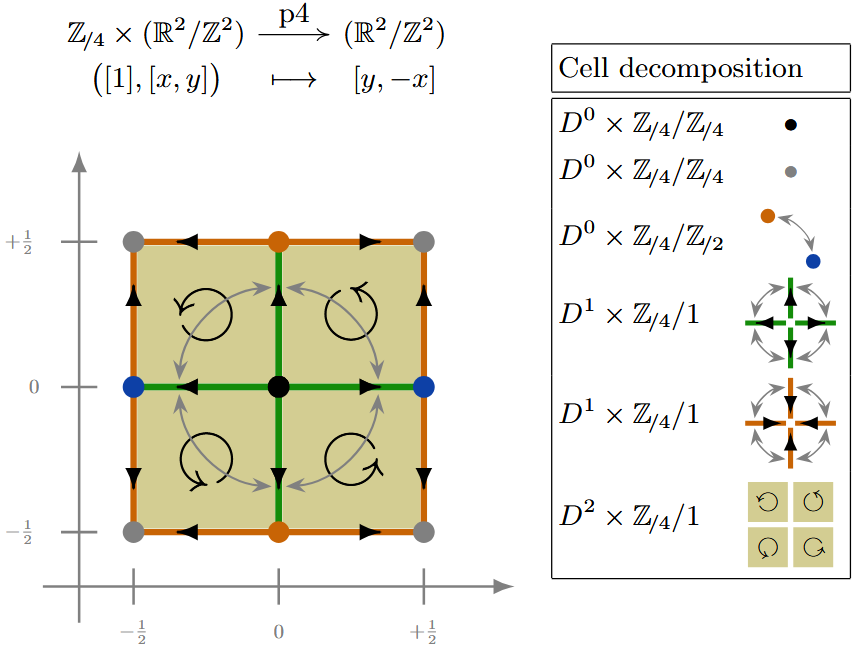
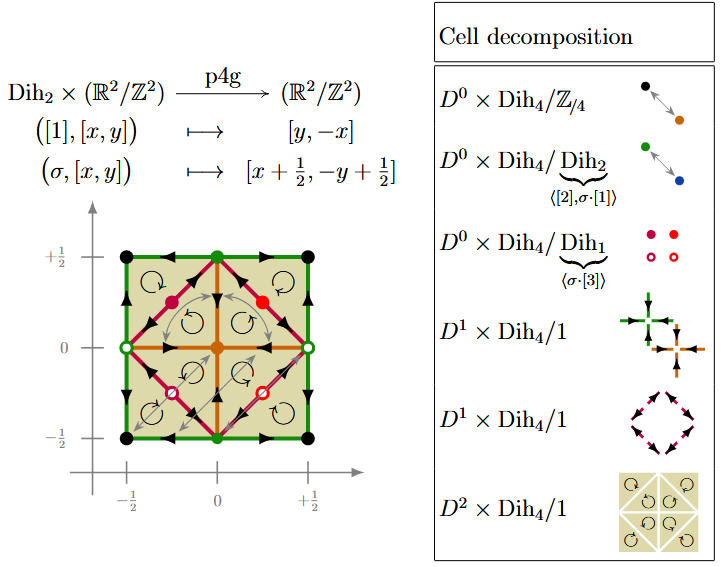
Example
(p4g) Here is a -CW complex structure for the torus equipped with rotation and glide reflection action corresponding to the wallpaper group :
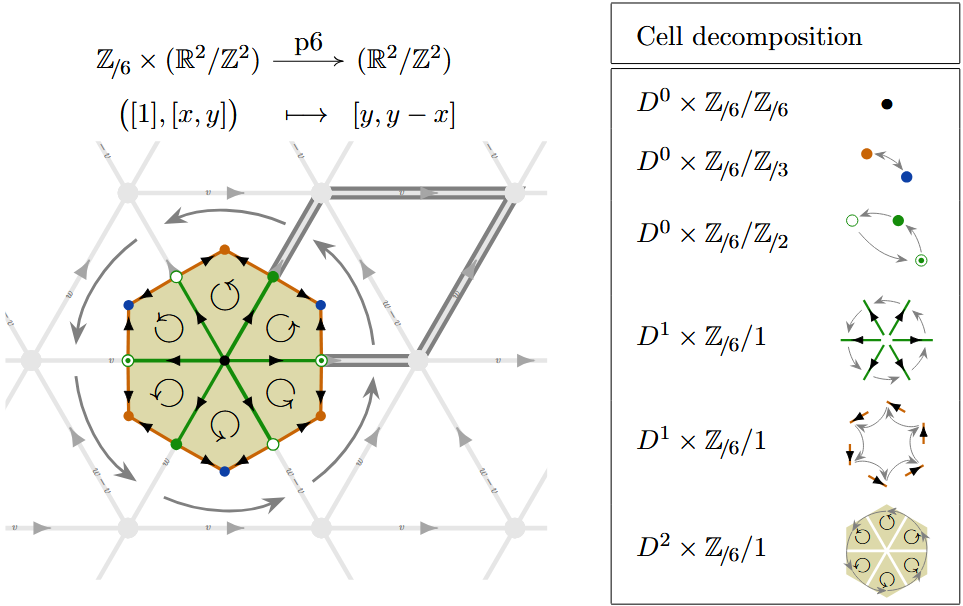
Example
(p6) Here is a -CW complex structure for the torus equipped with the -action which rotates by multiples of around the origin:
Related concepts
References
Review:
-
Doris Schattschneider: The plane symmetry groups and their recognition, American Mathematical Monthly 85 (1978) 439-450 [pdf, pdf]
-
Mark A. Armstrong, chapters 25-26 of: Groups and Symmetry, Undergraduate Texts in Mathematics, Springer (1988) [doi:10.1007/978-1-4757-4034-9, pdf]
-
Patrick Morandi: The Classification of Wallpaper Patterns: From Group Cohomology to Escherís Tessellations (2003) [pdf, pdf]
-
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss: The Symmetries of Things, CRC Press (2008) [ISBN:9781568812205]
-
Christopher Hammond, chapter 2 of: The Basics of Crystallography and Diffraction, Oxford University Press (2015) [ISBN:9780198738688]
-
Richard Tilley, Sec. 3.5 in: Crystals and Crystal Structure, Wiley (2020) [ISBN:978-1-119-54838-6]
-
Angela Zhao: A Brief Survey on Wallpaper Groups, MIT Mathematics (2023) [pdf]
See also:
- Wikipedia, Wallpaper group
Original discussion of the “orbifold notation” for (2D) space groups:
-
John H. Conway: The Orbifold Notation for Surface Groups, chapter 36 in: Groups, Combinatorics and Geometry, Cambridge University Press (1992) 438-447 [doi:10.1017/CBO9780511629259.038,
pdf]
-
John H. Conway, Daniel H. Huson: The Orbifold Notation for Two-Dimensional Groups, Structural Chemistry 13 3-4 (2002) 247–257 [doi:10.1023/A:1015851621002, pdf]
Discussion of meromorphic functions on the complex plane invariant under wallpaper groups:
- Richard Chapling, Invariant Meromorphic Functions on the Wallpaper Groups (arXiv:1608.05677)
Last revised on August 4, 2025 at 15:49:26. See the history of this page for a list of all contributions to it.