nLab exclusive disjunction

Idea

In propositional logic, the exclusive disjunction (also called exclusive or or simply xor) of a family of statements (truth values, propositions, predicates, velc) is a statement that is true if and only if exactly one of the statements in the family is true. The corresponding operation on subsets (of a fixed set) or material sets is called exclusive union, and the binary operation agrees with symmetric difference (which is generalised to higher arities in a different way). If we think of quantifiers as infinitary operators, then exclusive disjunction becomes uniqueness quantification.

Definitions

The exclusive disjunction of $p$ and $q$, written $p ⊻ q$ (and a host of other ways), may be defined in any of these forms: 1. $\neg(p \Leftrightarrow q)$, 2. $(p \vee q) \wedge (\neg p \vee \neg q)$, 3. $(p \wedge \neg{q}) \vee (\neg{p} \wedge q)$.

These are all equivalent in classical logic. In intuitionistic logic, (2,3) are equivalent but (1) is weaker; (2,3) give the usual meaning in constructive mathematics.

The false statement is the identity for this operation; it is the exclusive disjunction of no statements.

In classical logic (but not in intuitionistic logic), this operation is associative, but multiple applications don't mean what you may think. Instead, $(p ⊻ q) ⊻ r \equiv p ⊻ (q ⊻ r)$ comes out true if $p, q, r$ are all true; in general,

$$(p_1 ⊻ (p_2 ⊻ \cdots ⊻ p_n)\cdots)$$

is true if and only if an odd number of the statements $p_i$ is true. But when we write a multiple statement with ‘xor’, we really mean that exactly one of the statements is true. So by fiat, define the exclusive disjunction

$$p_1 ⊻ p_2 ⊻ \cdots ⊻ p_n$$

(without parentheses) to mean that exactly one of the $p_i$ is true; this definition is also used in intuitionistic logic.

As the indexed version of ordinary disjunction is existential quantification $\exists$, so the indexed version of exclusive disjunction is uniqueness quantification $\exists!$; this requires a primitive notion of equality to state in predicate logic.

Similarly, the exclusive union of two sets $A$ and $B$, written $A \uplus B$ (and a host of other ways), may be defined using exclusive disjunction:

$$A \uplus B = \{ x \;|\; x \in A \;⊻\; x \in B \} .$$

The exclusive union of a family $(A_i)_{i\colon I}$ of sets may be defined using uniqueness quantification:

$$\biguplus_i A_i = \{ x \;|\; \exists!{i},\; x \in A_i \} .$$

Note that the union, exclusive union, and (internal, or external up to natural isomorphism) disjoint union of a family of (pairwise) disjoint sets are all the same. For a family that is not disjoint, however, the union are exclusive union are different, the internal disjoint union does not make sense, and the external disjoint union is not isomorphic to either the union or the exclusive union (at least not naturally, and in some cases not at all).

We also have the symmetric difference of two sets, which is the same as the exclusive union. But we see this operation as the addition in a Boolean ring and so actually interpret it in the usual way as an associative operation. So the symmetric difference of $n$ sets indeed consists of those points that belong to an odd number of sets, and there is no infinitary symmetric difference.

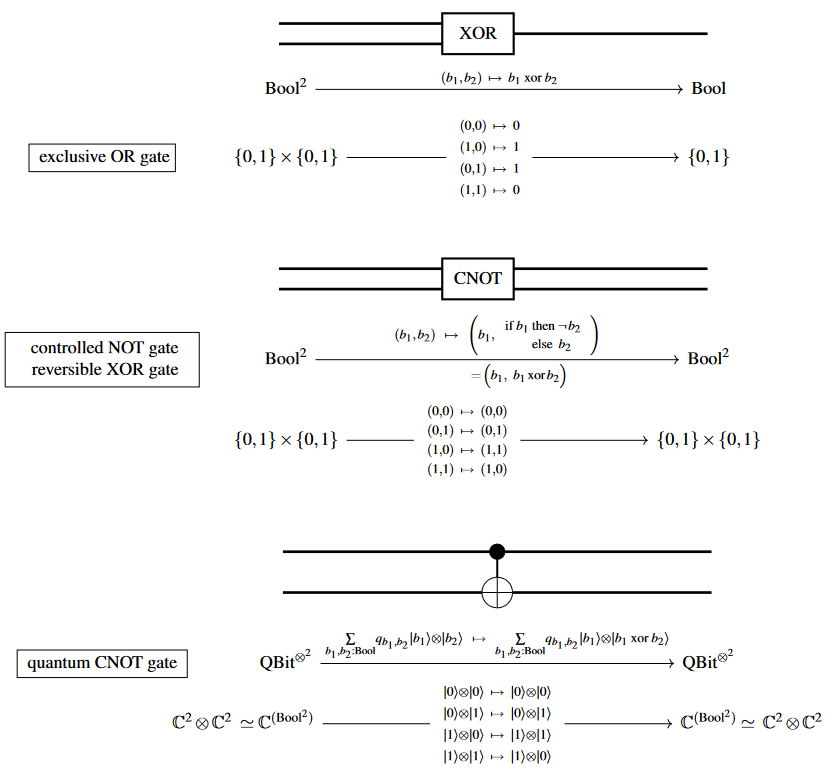
As a logic gate

Exclusive disjunction as a logic gate, a reversible gate (CNOT) and as a quantum logic gate:

In natural language

It is widely said that ‘or’ in English can mean either inclusive or exclusive disjunction, while Latin has two terms, respectively ‘vel’ and ‘aut’, but this is not really correct. It's more correct that ‘or’ can sometimes mean union and sometimes disjoint union (with the latter sometimes external and sometimes internal), but never symmetric difference. Thus, the only meaning of ‘or’ is for some kind of coproduct, which exclusive disjunction is not. (Similarly, ‘aut’ is more about disjoint union than symmetric difference.) In some cases, exclusive disjunction may be a valid implicature (in the sense of linguistic philosopher Paul Grice) even if the only valid inference (by the literal meaning of the sentence) is taken to be inclusive.

For the literature on this subject, see the Stanford Encylopedia entry and The Myth of the Exclusive ‘Or’ (Mind, 80 (317), 116–121).

Related concepts

• CNOT

• logic gate

References

See also

• Wikipedia, Exclusive or