nLab step function
Context
Functional analysis
Overview diagrams
Basic concepts
Theorems
Topics in Functional Analysis
Contents
Idea
Generally, a step function is a function from the real numbers to themselves which is constant everywhere except at one single point (or a finite number of points).
Specifically the function
is sometimes called the Heaviside step function.
This may be regarded as the generalized function-expression for the distributional density which sends a bump function to its integral over the positive half-axis:
As such is also called the Heaviside distribution.
The distributional derivative of the Heaviside distribution is the Dirac delta distribution (prop. below).
Properties
Proposition
The distributional derivative of the Heaviside distribution is the delta distribution :
Proof
For any bump function we compute:
Definition
(Fourier integral formula for step function)
The Heaviside distribution is equivalently the following limit of Fourier integrals (see at Cauchy principal value)
where the limit is taken over sequences of positive real numbers tending to zero.
Proof
We may think of the integrand uniquely extended to a holomorphic function on the complex plane and consider computing the given real line integral for fixed as a contour integral in the complex plane.
If is positive, then the exponent
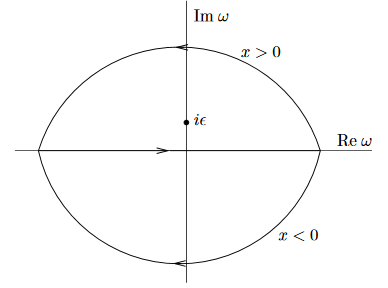
has negative real part for positive imaginary part of . This means that the line integral equals the complex contour integral over a contour closing in the upper half plane. Since has positive imaginary part by construction, this contour does encircle the pole of the integrand at . Hence by the Cauchy integral formula in the case one gets
Conversely, for the real part of the integrand decays as the negative imaginary part increases, and hence in this case the given line integral equals the contour integral for a contour closing in the lower half plane. Since the integrand has no pole in the lower half plane, in this case the Cauchy integral formula says that this integral is zero.
Remark
The Fourier form of the step function in prop. gives rise to the standard expression for the advanced propagator, retarded propagator and Feynman propagator used in perturbative quantum field theory. See at Feynman propagator for more.
Related concepts
References
- Wikipedia, Step function
Last revised on November 20, 2017 at 15:12:34. See the history of this page for a list of all contributions to it.