nLab perturbative quantum field theory
Context
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
“God does not do perturbation theory, perturbation theory is what we do because we don’t know any better.” [Duff 2020]
What is called perturbative quantum field theory (pQFT) is quantum field theory where the interaction (between fields/particles) is treated as a tiny perturbation of the “free field theory” where no interaction is assumed to take place (“perturbation theory”). This is meant to be an approximation to the actual non-perturbative quantum field theory. However, the latter remains elusive except for toy examples of low spacetime dimension, vanishing interaction and/or topological invariance and most of the “quantum field theory” in the literature is tacitly understood to be perturbative.
Hence pQFT studies the infinitesimal neighbourhood (also called the formal neighbourhood) of free classical field theories in the parameter space of all quantum field theories, the rest of the space being the realm of non-perturbative QFT:
Mathematically this means that the resulting quantum observables in pQFT (typically: scattering amplitudes or “S-matrices” encoded by Feynman diagrams) are formal power series in the coupling constant which measures the strength of the interaction (as well as in Planck's constant, which measures the general strength of quantum) effects. This distinguishes perturbative quantum field theory from non-perturbative quantum field theory, where the algebras of quantum observables are supposed to be not formal power series algebras, but C*-algebras.
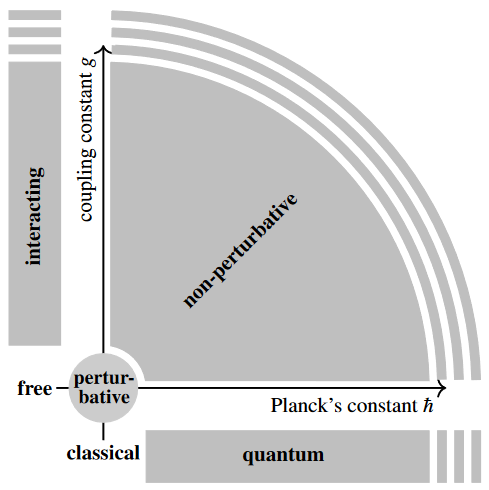
While just describing a tiny (infinitesimal) part of QFT, perturbative QFT is way better understood than full non-perturbative QFT (which remains ill-understood to the extent that it has been named a Millennium Problem), and has the reputation of still being dramatically successful in practice – though this applies to some field theories (such as QED) much more than to others (such as QCD), see below.
The key object of perturbative QFT is the perturbative scattering matrix which expresses, as a formal power series in the ratio of the coupling constant over Planck's constant, the probability amplitude of scattering processes, namely of processes where free fields in a certain state come in from the far past, interact and hence scatter off each other, and then go off in some other quantum state into the far future. The scattering cross sections thus defined are the quantities which may be directly measured in scattering experiments, such as the LHC accelerator.
The perturbative S-matrix turns out to have an expression as a sum over separate scattering amplitudes for elementary processes labeled by Feynman diagrams, each of which depicts one specific way for fields (particles) to interact with each other. That the full S-matrix is the sum over all amplitudes for all these possible scattering processes, the Feynman perturbation series, is an incarnation of the informal heuristic of the path integral and the superposition principle in quantum physics, which says that the probability amplitude for a specific outcome is the sum over the probability amplitudes of all the possible processes that can contribute to this outcome.
For all interesting interacting field theories, such as quantum electrodynamics and quantum chromodynamics, this scattering matrix formal power series necessarily has vanishing radius of convergence (Dyson 52). If it is assumed that the formal Feynman perturbation series is the Taylor series of an actual smooth function given by the actual non-perturbative quantum field theory that is being approximated, then this means that it is at least an asymptotic series (by this example) whose first couple of terms could sum to a good approximation of the actual value to be computed. Indeed, the sum of the first few loop orders in the S-matrix for QED and QCD in the standard model of particle physics turns out to be in agreement with experiment to good precision.
(There are however known non-perturbative effects which are not captured in perturbation theory, such as confinement in QCD, supposedly related to instantons in QCD. In resurgence theory one tries to identify these from the asymptotic nature of the Feynman perturbation series.)
A key step in the construction of perturbative quantum field theory is the renormalization of the point interactions. This comes about because given
-
a local Lagrangian density defining the nature of the fields and their interactions,
-
a vacuum state (generally: Hadamard state) that defines the free quantum field theory to be perturbed about
it turns out that the construction of the perturbative S-matrix (the Feynman perturbation series) still involves at each order a finite-dimensional space of choices to be made. Physically, these are the specification of further high energy interactions not seen in the original local Lagrangian density; mathematically, this is the choice of extending the time-ordered product of the interaction, which is an operator-valued distribution, to the locus of coinciding interaction points, in the sense of extensions of distributions.
Historically, perturbative quantum field theory as originally conceived informally by Schwinger-Tomonaga-Feynman-Dyson in the 1940s, had been notorious for the mysterious conceptual nature of its mathematical principles (“divergences”). The mathematically rigorous formulation of renormalization (“removal of UV-divergences”) in perturbative quantum field theory on Minkowski spacetime was established by Epstein-Glaser 73, based on Bogoliubov-Shirkov 59 and Stückelberg 51), now known as causal perturbation theory; laid out in the seminal Erice summer school proceeding (Velo-Wightman 76).
The correct definition of the adiabatic limit (“removal of IR divergencies”) was understood in Il’in-Slavnov 78 and eventually developed by Dütsch-Fredenhagen 01, Brunetti-DütschFredenhagen 09, this is now called perturbative algebraic quantum field theory. The rigorous derivation of the previously informal Feynman rules and their dimensional regularization for computation of scattering amplitudes was achieved in Keller 10 (IV.12), Dütsch-Fredenhagen-Keller-Rejzner 14. Quantization of gauge theories (Yang-Mills theory) in causal perturbation theory/perturbative AQFT was then discussed (for trivial principal bundles and restricted to gauge invariant observables) in the spirit of BRST-complex/BV-formalism in (Fredenhagen-Rejzner 11b). The generalization of all these constructions from Minkowski spacetime to perturbative quantum fields on more general spacetimes (i.e. for more general gravitational background fields such as appearing in cosmology or black hole physics) was made possible due to the identification of the proper generalization of vacuum states and their Feynman propagators to Hadamard states on globally hyperbolic spacetimes in Radzikowski 96. The resulting rigorous perturbative QFT on curved spacetimes was developed in a long series of articles by Hollands, Wald, Brunetti, Fredenhagen and others, now called locally covariant perturbative AQFT.
While this establishes a rigorous construction of perturbative quantum field theory on general gravitational backgrounds, the construction principles had remained somewhat ad-hoc: The axioms for the perturbative S-matrix (equivalently for the time-ordered products or retarded products of field operators) were well motivated by comparison with the Dyson series in quantum mechanics, by the heuristics of the path integral and not the least by their excellent confirmation by experiment, but had not been derived from first principles of quantization. Then in Dütsch Fredenhagen 01 it was observed that the Wick algebras of quantum observables in free quantum field theory are equivalently the Moyal deformation quantization of the canonical Poisson bracket (the Peierls bracket or causal propagator) on the covariant phase space of the free field theory (or rather of a choice of Hadamard state for it) and Collini 16 showed that under suitable conditions the perturbative interacting observable algebra is the Fedosov deformation quantization of covariant phase space of the interacting theory. A general argument to this extent was given in Hawkins-Rejzner 16.
This suggests that the construction of the full non-perturbative quantum field theory ought to be given by a strict deformation quantization of the covariant phase space. But presently no example of such for non-trivial interaction in spacetime dimension is known. In particular the phenomenologically interesting case of a complete construction of interacting field theories on 4-dimensional spacetimes is presently unknown. For the case of Yang-Mills theory this open problem to go beyond perturbative quantum field theory is one of the “Millennium Problems” (see at quantization of Yang-Mills theory). For the case of quantum gravity this is possibly the -year problem that the field is facing. But observe that as a perturbative (effective“) quantum field theory, quantum gravity does fit into the framework of perturbative QFT, is mathematically well-defined and makes predictions, see the references there.
Details
A comprehensive introduction is at geometry of physics – perturbative quantum field theory.
Properties
Related concepts
References
General
The original informal conception of perturbative QFT is due to Schwinger-Tomonaga-Feynman-Dyson:
- Freeman Dyson, The raditation theories of Tomonaga, Schwinger and Feynman, Phys. Rev. 75, 486, 1949 (pdf)
Non-rigorous but widely used textbooks:
-
James D. Bjorken, Sidney D. Drell: Relativistic Quantum Mechanics, McGrawHill (1964) [ark:/13960/t5fc2v05h, pdf, pdf]
-
James D. Bjorken, Sidney D. Drell: Relativistic Quantum Fields, McGraw-Hill (1965) [ark:/13960/t9t22sx2r, pdf]
-
Michael Peskin, Daniel Schroeder: An Introduction to Quantum Field Theory, CRC Press (1995) [doi:10.1201/9780429503559, spire:407703, ISBN 9780201503975]
-
Steven Weinberg, The Quantum Theory of Fields Vol 1: Foundations, Cambridge University Press (1995) [doi:10.1017/CBO9781139644167]
-
Steven Weinberg, The Quantum Theory of Fields Vol 2: Applications, Cambridge University Press (1996) [doi:10.1017/CBO9781139644174]
The rigorous formulation of renormalized perturbative quantum field theory in terms of causal perturbation theory was first accomplished in
- Henri Epstein, Vladimir Glaser, The Role of locality in perturbation theory, Annales Poincaré Phys. Theor. A 19 (1973) 211 (Numdam)
with precursors in
-
Ernst Stückelberg, D. Rivier, Helv. Phys. Acta, 22 (1949) 215.
-
Ernst Stückelberg, J. Green, Helv. Phys. Acta, 24 (1951) 153.
-
Ernst Stückelberg, A. Peterman, , La normalisation des constants dans la theorie des quanta, Helv. Phys. Acta 26, 499 (1953);
-
Nikolay Bogoliubov, Dmitry Shirkov, Introduction to the Theory of Quantized Fields, New York (1959)
Traditional review includes:
-
Matthew Schwartz, Quantum Field Theory and the Standard Model, Cambridge University Press (2014) [ISBN:9781107034730, doi:10.1017/9781139540940, front matter:pdf]
-
Michel Talagrand, What is a Quantum Field Theory? – A first Introduction for Mathematicians, Cambridge University Press (2022) [doi:10.1017/9781108225144]
A seminal compilation of the resulting rigorous understanding of renormalization is
- G. Velo and Arthur Wightman (eds.): Renormalization Theory, Proceedings of the 1975 Erice summer school, NATO ASI Series C 23, D. Reidel, Dordrecht, 1976
Concrete computations in rigorous causal perturbation theory have been spelled out for quantum electrodynamics in
- Günter Scharf, Finite Quantum Electrodynamics – The Causal Approach, Berlin: Springer-Verlag, 1995, 2nd edition
and for Yang-Mills theory, quantum chromodynamics and perturbative quantum gravity in
- Günter Scharf, Quantum Gauge Theories – A True Ghost Story, Wiley 2001
The treatment of the IR-divergencies by organizing the perturbative quantum observables into a local net of observables was first suggested in
- V. A. Il’in and D. S. Slavnov, Observable algebras in the S-matrix approach, Theor. Math. Phys. 36 (1978) 32 (spire, doi)
and then developed to perturbative algebraic quantum field theory in
-
Michael Dütsch, Klaus Fredenhagen, Algebraic Quantum Field Theory, Perturbation Theory, and the Loop Expansion, Commun. Math. Phys. 219 (2001) 5-30 (arXiv:hep-th/0001129)
-
Romeo Brunetti, Michael Dütsch, Klaus Fredenhagen, Perturbative Algebraic Quantum Field Theory and the Renormalization Groups, Adv. Theor. Math. Physics 13 (2009), 1541-1599 (arXiv:0901.2038)
Quantization of gauge theories (Yang-Mills theory) in causal perturbation theory/perturbative AQFT is discussed (for trivial principal bundles and restricted to gauge invariant observables) in the spirit of BRST-complex/BV-formalism in
-
Klaus Fredenhagen, Kasia Rejzner, Batalin-Vilkovisky formalism in the functional approach to classical field theory, Commun. Math. Phys. 314(1), 93–127 (2012) (arXiv:1101.5112)
-
Klaus Fredenhagen, Kasia Rejzner, Batalin-Vilkovisky formalism in perturbative algebraic quantum field theory, Commun. Math. Phys. 317(3), 697–725 (2012) (arXiv:1110.5232)
and surveyed in:
-
Kasia Rejzner, section 7 of Perturbative Algebraic Quantum Field Theory, Springer 2016
-
Urs Schreiber, geometry of physics – perturbative quantum field theory, 2017
-
Michael Dütsch, From classical field theory to perturbative quantum field theory, 2018
The generalization of all these constructions to quantum fields on general globally hyperbolic spacetimes (perturbative AQFT on curved spacetimes) was made possible by the results on Hadamard states and Feynman propagators in
- Marek Radzikowski, Micro-local approach to the Hadamard condition in quantum field theory on curved space-time, Commun. Math. Phys. 179 (1996), 529–553 (Euclid)
and then developed in a long series of articles by Stefan Hollands, Robert Wald, Romeo Brunetti, Klaus Fredenhagen and others. For this see the references at AQFT on curved spacetimes.
The observation that perturbative quantum field theory is equivalently the formal deformation quantization of the defining local Lagrangian density is for free field theory due to
-
Michael Dütsch, Klaus Fredenhagen, Perturbative algebraic quantum field theory and deformation quantization, Proceedings of the Conference on Mathematical Physics in Mathematics and Physics, Siena June 20-25 (2000) (arXiv:hep-th/0101079)
-
A. C. Hirshfeld, P. Henselder, Star Products and Perturbative Quantum Field Theory, Annals Phys. 298 (2002) 382-393 (arXiv:hep-th/0208194)
and for interacting field theories (causal perturbation theory/perturbative AQFT) due
-
Giovanni Collini, Fedosov Quantization and Perturbative Quantum Field Theory (arXiv:1603.09626)
-
Eli Hawkins, Kasia Rejzner, The Star Product in Interacting Quantum Field Theory (arXiv:1612.09157)
For more see the references at perturbative algebraic quantum field theory.
The relation of the construction via causal perturbation theory to the Feynman perturbation series in terms of Feynman diagrams was understood in
-
Jose Gracia-Bondia, S. Lazzarini, Connes-Kreimer-Epstein-Glaser Renormalization (arXiv:hep-th/0006106)
-
Kai Keller, chapter IV of Dimensional Regularization in Position Space and a Forest Formula for Regularized Epstein-Glaser Renormalization, PhD thesis (arXxiv:1006.2148)
-
Michael Dütsch, Klaus Fredenhagen, Kai Keller, Katarzyna Rejzner, Dimensional Regularization in Position Space, and a Forest Formula for Epstein-Glaser Renormalization, J. Math. Phy.
55(12), 122303 (2014) (arXiv:1311.5424)
(…)
Non-convergence of the perturbation series
The argument that the perturbation series of realistic pQFTs necessarily diverges, in fact has vanishing radius of convergence (is at best an asymptotic series) goes back to
- Freeman Dyson, Divergence of perturbation theory in quantum electrodynamics, Phys. Rev. 85, 631, 1952 (spire)
and is made more precise in
- Lev Lipatov, Divergence of the Perturbation Theory Series and the Quasiclassical Theory, Sov.Phys.JETP 45 (1977) 216–223 (pdf)
recalled for instance in
-
Igor Suslov, section 1 of Divergent perturbation series, Zh.Eksp.Teor.Fiz. 127 (2005) 1350; J.Exp.Theor.Phys. 100 (2005) 1188 (arXiv:hep-ph/0510142)
-
Justin Bond, last section of Perturbative QFT is Asymptotic; is Divergent; is Problematic in Principle (pdf)
-
Mario Flory, Robert C. Helling, Constantin Sluka, How I Learned to Stop Worrying and Love QFT [arXiv:1201.2714]
-
Franco Strocchi, §2.2 of: An Introduction to Non-Perturbative Foundations of Quantum Field Theory, Oxford University Press (2013) [doi:10.1093/acprof:oso/9780199671571.001.0001]
-
Stefan Hollands, Robert Wald, Section 4.1 of: Quantum fields in curved spacetime, Physics Reports 574 (2015) 1-35 [arXiv:1401.2026, doi:10.1016/j.physrep.2015.02.001]
-
Marco Serone, from 2:46 on in A look at using perturbation theory (recording)
The argument that the perturbation series should be trustworthy for number of terms smaller than the inverse of the coupling constant is recalled in Flory, Helling & Sluka 2012, p. 8 & eq. (34) & Sec. 2.5.
Exposition also in:
For the example of -theory this non-convergence of the perturbation series is discussed in
-
Robert C. Helling, p. 4 of Solving classical field equations (pdf, pdf)
-
Alexander P. Bakulev, Dmitry Shirkov, section 1.1 of Inevitability and Importance of Non-Perturbative Elements in Quantum Field Theory, Proceedings of the 6th Mathematical Physics Meeting, Sept. 14–23, 2010, Belgrade, Serbia (ISBN 978-86-82441-30-4), pp. 27–54 (arXiv:1102.2380)
See also
- Carl M. Bender, Carlo Heissenberg, Convergent and Divergent Series in Physics (arXiv:1703.05164)
And see at perturbation theory – On divergence/convergence
Discussion of further issues, even when resummation is thought to apply, arising for n-point functions at large (large number of external particles in a scattering process):
failure of unitarity (for -theory):
- Sebastian Schenk, The Breakdown of Resummed Perturbation Theory at High Energies (arXiv:2109.00549)
failure of locality (for perturbative quantum gravity and perturbative string theory):
-
Sudip Ghosh, Suvrat Raju, Loss of locality in gravitational correlators with a large number of insertions, Phys. Rev. D 96, 066033 (2017) (arXiv:1706.07424)
-
Sudip Ghosh, Suvrat Raju, The Breakdown of String Perturbation Theory for Many External Particles, Phys. Rev. Lett. 118, 131602 (2017) (arXiv:1611.08003)
L-infinity algebra structure
Further identification of L-infinity algebra-structure in the Feynman amplitudes/S-matrix of Lagrangian perturbative quantum field theory:
-
Markus Fröb, Anomalies in time-ordered products and applications to the BV-BRST formulation of quantum gauge theories (arXiv:1803.10235)
-
Alex Arvanitakis, The -algebra of the S-matrix (arXiv:1903.05643)
Last revised on August 16, 2024 at 06:28:57. See the history of this page for a list of all contributions to it.