nLab Fredholm operator

Definition

Definition

A bounded linear operator $F \colon B_1\to B_2$ between Banach spaces is Fredholm if it has finite dimensional kernel and finite dimensional cokernel.

(e.g. Murphy 1990 p. 23)

Remark

Some (older) text may also require that the image of $F$ be closed, but that is in fact implied by the cokernel of $F$ having finite dimension (cf. Prop. below). Moreover, some (older) texts do not require $F$ to be bounded, but just ask that it be closed with dense domain of definition (e.g. Schechter 1967 §1).

Definition

The difference between the dimensions of the kernel and the cokernel of a Fredholm operator $F$ is called its index (the Fredholm index)

$$\begin{array}{ccl} ind F &\coloneqq& dim (ker F) - dim (coker F) \\ &=& dim (ker F) - codim (im F) \mathrlap{\,.} \end{array}$$

Examples

• Elliptic operators on compact manifolds are naturally Fredholm, when understood between the appropriate Sobolev spaces.

• charged vacua of free Dirac field in Coulomb background are characterized by Fredholm operators

Properties

General

Proposition

The image (range) of a Fredholm operator is closed.

(cf. Murphy 1990 Thm. 1.4.7)

Proposition

The topological subspace $Fred(B_1,B_2)\subset B(B_1,B_2)$ of Fredholm operators (in the space of bounded linear operators equipped with the norm topology) is open.

On this subspace with its subspace topology, the Fredholm index (Def. ) is a continuous map.

(Murphy 1990 Thm. 1.4.17)

Remark

In other words, Prop. says that given a Fredholm operator $F$ then there exists a real number $\epsilon \gt 0$ such that every bounded linear operator $G$ with operator norm ${\Vert G - F \Vert} \lt \epsilon$ is itself Fredholm of the same index.

Proposition

For Banach spaces $B_1$, $B_2$, $B_3$ and Fredholm operators $F_1 \colon B_1 \longrightarrow B_2$ and $F_2 \colon B_2 \longrightarrow B_3$

1. the composite $F_2 \,\circ\, F_1 \colon B_1 \longrightarrow B_3$ is Fredholm

2. with index (Def. ) the sum of the indices of the factors:

   $$ind(F_2\circ F_1) \;=\; ind(F_1) + ind(F_2) \,.$$

(Murphy 1990 Thm. 1.4.8)

Remark

In other words, Prop. says that Banach spaces with Fredholm operators between them form a category on which the Fredholm index is a functor to the delooping groupoid of the integers; hence the endomorphic Fredholm operators $F \colon B \longrightarrow B$ form a monoid with the Fredholm index being a homomorphism of monoids.

Via parametrices

An equivalent characterization of Fredholm operators is the following:

Definition

A parametrix of a bounded linear operator $F \colon \mathcal{H}_1 \to \mathcal{H}_2$ is a reverse bounded operator $P \colon \mathcal{H}_2 \to \mathcal{H}_1$ which is an “inverse up to compact operators”, i.e. such that $F \circ P - id_{\mathcal{H}_2}$ and $P \circ F - id_{\mathcal{H}_1}$ are both compact operators.

Proposition

(Atkinson's theorem)
A bounded linear operator $F \colon B_1\to B_2$ between Banach spaces is Fredholm, def. , precisely if it admits a parametrix, def. .

(cf. Murphy 1990 Thm. 1.4.16)

Relation to topological K-theory

Proposition

(Atiyah-Jänich theorem)
The space of Fredholm operators $Fred(\mathscr{H})$ on a (countably infinite-dimensional, separable, complex) Hilbert space $\mathscr{H}$ is a classifying space for topological K-theory $K(-)$:

For $X$ a compact Hausdorff space, the homotopy classes of continuous maps from $X$ to $Fred(\mathscr{H})$ are in natural bijection with $K(X)$

$$\pi_0 \, Map\big( X, \, Fred(\mathscr{H}) \big) \xrightarrow[\sim]{ind_X} K(X) \,,$$

where $ind_X$ is an $X$-parameterized enhancement of the Fredholm index.

Several variants of the ordinary space of Fredholm operators retain the same homotopy type and hence all serves as classifying spaces for topological K-theory, but differ in further properties they have, cf. Atiyah & Segal 2004 §3.

A definition which makes a good classifying space also for twisted K-theory and equivariant K-theory is the following:

Definition

Given any $C_2$-graded infinite-dimensional (separable complex) Hilbert space $\mathscr{H} \simeq \mathscr{H}_+ \oplus \mathscr{H}_i$, write $Fred^{(0)}(\mathscr{H})$ for the set of bounded linear operators $F \,\colon\, \mathscr{H} \to \mathscr{H}$ which are

1. self-adjoint: $F^\dagger = F$

2. odd-graded: $F(\mathscr{H}_{\pm}) \subset \mathscr{H}_{\mp}$,

3. idempotent up to compact operators: $F^2 - Id \,\in\, \mathcal{K}(\mathscr{H})$,

equipped with the topology of the topological subspace, via

$$F \,\mapsto\, \big(F ,\, F^2 - id\big) \,,$$

of the product space of the spaces of

1. bounded linear operators, $\mathcal{B}$, equipped with the compact-open topology and

2. compact operators, $\mathcal{K}$, equipped with the norm topology:

(This is due to Atiyah & Segal 2004 Def. 3.2, following Atiyah & Singer 1969 p 7, see also Freed, Hopkins & Teleman 2011 Def. A.39.)

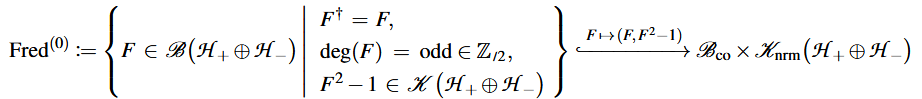
Remark

In view of Def. and Prop. , the condition $F^2 - id \in \mathcal{K}$ in Def. asserts that $F$ not just has a parametrix, but is its own parametrix. Or rather, together with the condition that $F$ is odd, hence $F = F_+ + F_-$ with $F_\pm \colon \mathscr{H}_{\pm} \to \mathscr{H}_{\mp}$, it says that $F_+$ and $F_-$ are parametrices of each other.

Indeed the Fredholm index map on $Fred^{(0)}(\mathscr{H})$ assigns the Fredholm index (Def. ) of one of these components (say $F_+$). (This follows by tracing through the equivalences indicated in AS04 §3.)

Finally, together with the grading, the condition $F^\ast = F$ implies that in fact $F_\pm = (F_\mp)^\ast$, whence the index is actually just (the dimension of) the kernel of $F$, but regarded as (the dimension of) a virtual vector space.

Generalizations

Fredholm operators generalize to Fredholm complexes. A finite chain complex

$$0 \to C_0 \stackrel{d_0}\to C_1\stackrel{d_1}\to C_2 \ldots C_n\to 0$$

of Banach spaces and bounded operators is said to be a Fredholm complex if the images $d_i$ are closed and the chain homology of the complex is finite dimensional. The Euler characteristic (the alternative sum of the dimensions of the homology groups) is then called the index of the Fredholm complex. Each Fredholm operator can be considered as a Fredholm complex concentrated at zero. Each Fredholm complex produces a Fredholm operator from the sum of the even- to the sum of the odd-numbered spaces in the complex.

One can consider Fredholm almost complexes, where $d_i \circ d_{i-1}$ is not zero but the image of that operator is compact. Out of every Fredholm almost complex one can make a complex by correcting the differentials by compact perturbation terms. Elliptic complexes give examples of Fredholm complexes.

Related concepts

• Fredholm module,

• Fredholm determinant,

• Dirac operator,

• Toeplitz operator

• K-theory, KK-theory

• index theory

References

Textbook accounts:

• Gerard Murphy: §1.4 in: $C^\ast$-algebras and Operator Theory, Academic Press (1990) [doi:10.1016/C2009-0-22289-6]

• William Arveson, §3.3 of: A Short Course on Spectral Theory, Graduate Texts in Mathematics 209, Springer (2002) [doi:10.1007/b97227]

Review:

• Martin Schechter: Basic theory of Fredholm operators, Annali della Scuola Normale Superiore di Pisa - Scienze Fisiche e Matematiche, Serie 3, 21 2 (1967) 261-280 [numdam:ASNSP_1967_3_21_2_261_0]

• Ethan Y. Jaffe: Atkinson’s Theorem [pdf]

  (focus on Atkinson's theorem)

Discussion of the space of Fredholm operators as a classifying space for topological K-theory:

• Michael Atiyah, Appendix of: K-theory, Harvard Lecture 1964 (notes by D. W. Anderson), Benjamin (1967) [pdf, pdf]

and variants that serve as classifying spaces also for twisted K-theory and equivariant K-theory:

• Michael Atiyah, Isadore Singer: Index theory for skew-adjoint Fredholm operators, Publications Mathématiques de l’Institut des Hautes Scientifiques 37 1 (1969) 5-26 [doi:10.1007/BF02684885, pdf]

• Michael Atiyah, Graeme Segal, §3 in: Twisted K-theory, Ukrainian Math. Bull. 1 3 (2004) [arXiv:math/0407054, journal page, published pdf]

• Daniel Freed, Michael Hopkins, Constantin Teleman, §A.5 in: Loop Groups and Twisted K-Theory I, J. Topology 4 (2011) 737-789 [arXiv:0711.1906, doi:10.1112/jtopol/jtr019]

See also:

• Wikipedia, Fredholm operator

• A. S. Mishchenko, Векторные расслоения и их применения (Vector bundles and their applications), Nauka, Moscow, 1984. 208 pp. MR87f:55010

• S. Rempel, B-W. Schulze, Index theory of elliptic boundary problems, Akademie–Verlag, Berlin, 1982.

• Lars Hörmander, The analysis of linear partial differential operators. III. Pseudo-differential operators, 1994, reprinted 2007.

• Pietro Aiena, Fredholm and local spectral theory, with applications to multipliers, book page

• Otgonbayar Uuye, A simple proof of the Fredholm Alternative, arxiv/1011.2933

• Alexander Grothendieck, La théorie de Fredholm, Bulletin de la Société Mathématique de France 84 (1956), p. 319-384, numdam

• Marina Prokhorova, Spectral Sections, arXiv:2008.04672.

• Marina Prokhorova, Spaces of unbounded Fredholm operators. I. Homotopy equivalences, arXiv:2110.14359.

• Marina Prokhorova, The continuity properties of discrete-spectrum families of Fredholm operators, arXiv:2201.09869.

• Marina Prokhorova, From graph to Riesz continuity, arXiv:2202.03337.

For Fredholm complexes, see

• Graeme Segal, Fredholm complexes, Quarterly Journal of Mathematics 21:4 (1970), 385–402. doi.

category: analysis