nLab tangent function
Context
Trigonometry
Contents
Idea
In trigonometry, the tangent function “” is one of the basic trigonometric functions.
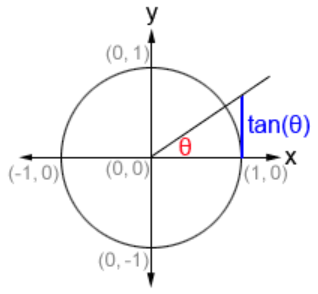
The tangent function may be understood as computing the length of the segment (shown in blue) of a tangent (whence the name) to a unit circle inside the Euclidean plane, between its point of tangency and its intersection with any radial line, as a function of the angle between that radial line and the one orthogonal to the tangent.
Since, by definition of the sine function “” and the cosine function “”, that radial line has distance from the perpendicular line where it crosses the unit circle at along that perpendicular line, the length of that tangential line segment equals the ratio , and this is how the tangent function is often defined.
Definition
The tangent function is the ratio of the sine and the cosine, where this is defined:
Properties
-
The tangent function is of course odd, and obeys a functional equation (‘addition formula’)
-
The hyperbolic analog , related to the tangent by
arises in special relativity theory in connection with rapidity.
-
The MacLaurin series for the tangent function arises in enumerative combinatorics, especially when bundled with the secant function?. Here the sum
is the exponential generating function of a sequence of natural numbers that count “zigzag permutations” on the set , i.e., permutations where . The tangent numbers, which are the coefficients when is odd, are related to Bernoulli numbers through the formula
They are related to values of the zeta function by the formula
Both of these facts may be verified by putting together corresponding facts for the cotangent function (see there) with the double angle formula
Related concepts
References
-
Wikipedia, Trigonometric functions – tan
-
Mathnet, tangent
Last revised on January 3, 2024 at 01:11:20. See the history of this page for a list of all contributions to it.