nLab tangent

From Do Carmo 1976

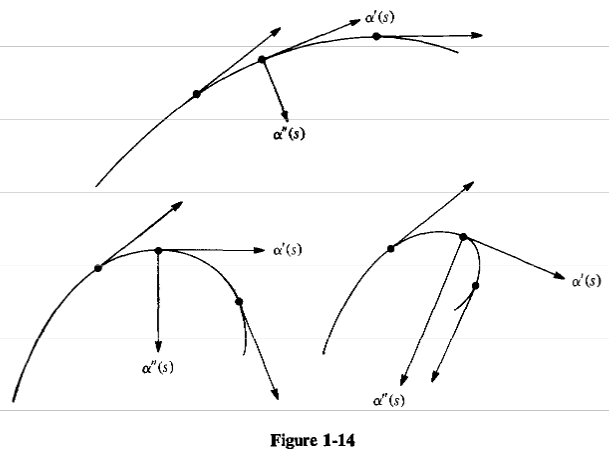
In the differential geometry of curves and surfaces, the tangent at a point on a smooth curve in the Euclidean plane is the straight line through that point whose slope is that of the curve at that point. Unless the curve is actually itself “straight” in a vicinity of the point, the tangent is the unique straight line which in an open neighbourhood of the point on the curve has exactly that one point in common with the curve. In any case, the tangent to a curve may be thought of as the best approximation by a straight line of that curve at the given point.

From math.net

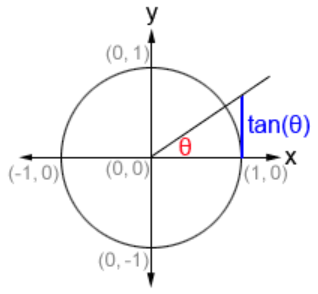
In trigonometry one considers such tangents in the Euclidean plane for the case that the curve is a unit circle. Here the tangent to a point on the circle may also be understood as the unique straight line through that point which makes a right angle with the “radial” line through that point and the center of the circle.

The length of the segment of a tangent to a unit circle between its point of tangency and its intersection with any other radial line is, as a function of the angle between the two radial lines, known as the tangent function, traditionally denoted “$tan(-)$”.

From Hatcher

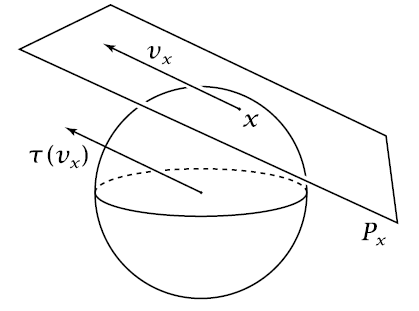
More generally in differential geometry, for a smooth manifold embedded inside a Euclidean space, a tangent line through a point on the manifold is a straight line in the ambient Euclidean space through that point which is the “best approximation” of the manifold by a straight line “at that point and in that direction”.

This is made precise by the notion of tangent vectors, which may be understood as infinitesimal tangent lines to a smooth manifold and are as such independent of a choice of embedding. The collection of tangent vectors to a manifold is thus known as its tangent bundle.

More generally but analogously there are higher dimensional tangent planes and tangent hypersurfaces which infinitesimally are given by tangent multivectors.

Related concepts

• slope of a line, direction of a vector

tangents…

• in differential geometry: tangent vector

• in trigonometry: tangent function

References

Most texts on differential geometry discuss tangents, for instance

• Manfredo P. Do Carmo, §1-5 in: Differential Geometry of Curves and Surfaces, Prentice-Hall (1976) [pdf]

• Victor A. Toponogov, §1.3 in: Differential Geometry of Curves and Surfaces — A Concise Guide, Springer (2006) [doi:10.1007/b137116]

See also:

• Wikipedia, Tangent

• math.net, tangent

category: disambiguation