nLab Pontrjagin-Thom collapse map
Context
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Contents
Idea
Given an embedding of smooth manifolds of codimension , the Thom collapse map (Thom 54) is the continuous function from to the n-sphere which assigns asymptotic normal distance from the submanifold, measured
-
in direction perpendicular to the submanifold, with respect to a normal framing;
-
asymptotically, regarding all points outside a tubular neighbourhood as being at infinity.
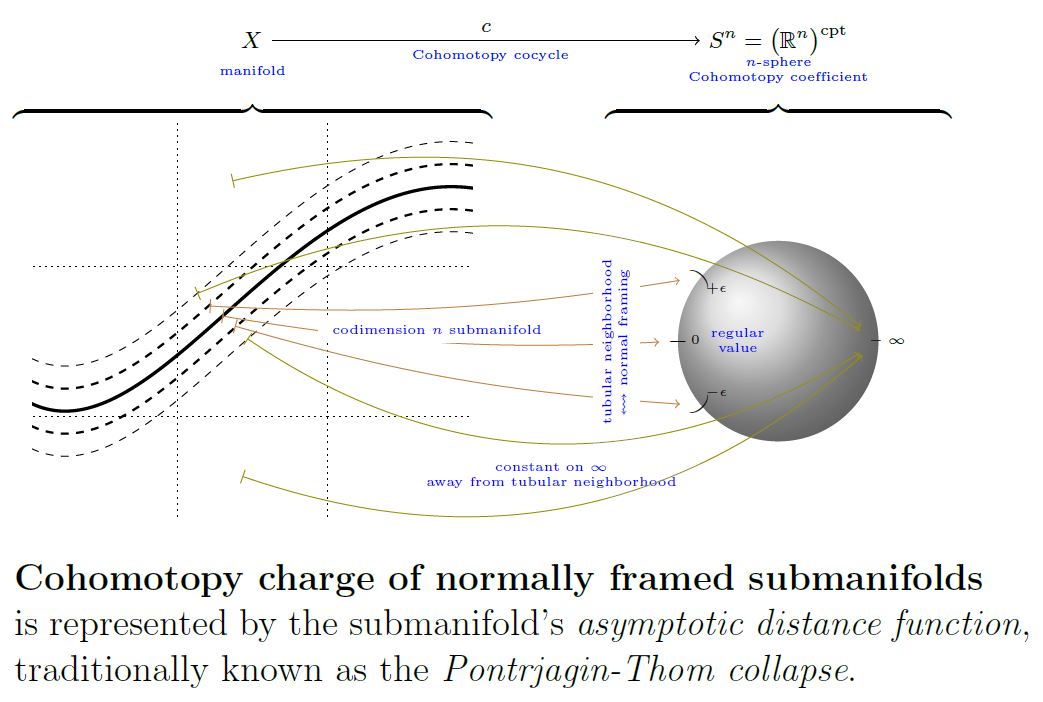
graphics grabbed from SS 19
For maximal codimension , hence for 0-dimensional submanifolds, hence for configurations of points, this is alternatively known as the “electric field map” (Salvatore 01 following Segal 73, Section 1, see also Knudsen 18, p. 49) or the “scanning map” (Kallel 98).
The homotopy class of the Thom collpase map may be regarded as the Cohomotopy charge of the submanifolds, as measured in -Cohomotopy-cohomology theory.
The PT collapse is a useful approximation to the would-be left inverse of the embedding of topological spaces
As such, it is is used to define pushforward of cohomology-classes along (“Umkehr maps”). It also appears as the key step in Thom's theorem.
Definition
Component definition in topological spaces
All topological spaces in the following are taken to be compact.
Consider and two manifolds and
an embedding.
Write
-
for the normal bundle;
-
for the Thom space of the normal bundle;
-
for any choice of tubular neighbourhood of .
Definition
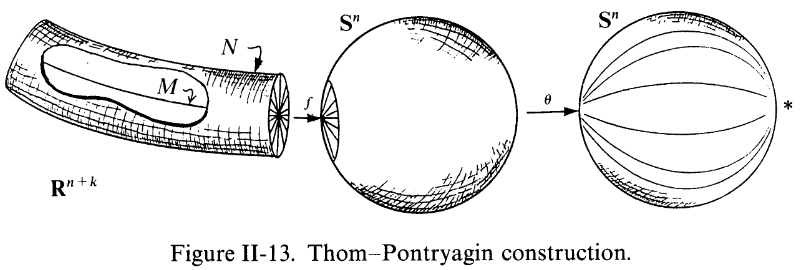
The collapse map (or the Pontrjagin-Thom construction) associated to and the choice of tubular neighbourhood is
where the first morphism is the projection onto the quotient and the second is the canonical homeomorphism to the Thom space of the normal bundle.
Remark
Since in the construction of remark every point of is associated to a particular point of , the collapse map lifts to a map
from to the smash product of the Thom space (canonically regarded as a pointed topological space) and the topological space with a base point adjoined.
(e.g. Rudyak 98, p. 317)
Example
Of particular interest is the case where in the above is a Cartesian space or rather its one-point compactification, the sphere . By the Whitney embedding theorem, for every there exists an such that every manifold of dimension has an embedding . In this case the collapse map of def. has the form
Composing this further with the canonical map to the universal vector bundle of rank yields a map
from to the th space in the Thom spectrum . This hence defines an element in the homotopy group of the Thom spectrum. Thom's theorem says that all elements in the homotopy groups of arise this way, and that they retain precisely the information of the cobordism equivalence class of manifolds .
In this case the refined Thom collapse map of def. is of the form
Remark
The refined map in example lifts to a morphism of spectra
where denotes the sphere spectrum and now the Thom spectrum of the normal bundle.
This morphism is the unit of an adjunction which exhibits the suspension spectrum as a dualizable object in the stable homotopy category, with dual object . See at Atiyah duality and at n-duality.
Equivalently, one may proceed as follows. For a framed manifold i.e. a manifold with a chosen trivialization of the normal bundle in some one has where is the union of with a disjoint base point. Identify a sphere with a one-point compactification . Then the Pontrjagin-Thom construction is the map obtained by collapsing the complement of the interior of the unit disc bundle to the point corresponding to and by mapping each point of to itself. Thus to a framed manifold one associates the composition
and its homotopy class defines an element in .
Abstract definition in terms of duality
The following is a more abstract description of Pontryagin-Thom collapse in the stable homotopy theory of sphere spectrum-(∞,1)-module bundles.
Definition
Write
for the Spanier-Whitehead duality map which sends a topological space first to its suspension spectrum and then that to its dual object in the (∞,1)-category of spectra.
Proposition
For a compact manifold, let be an embedding and write for the classical Pontryagin-Thom collapse map for this situation, and write
for the corresponding looping map from the sphere spectrum to the Thom spectrum of the negative tangent bundle of . Then Atiyah duality produces an equivalence
which identifies the Thom spectrum with the dual object of in and this constitutes a commuting diagram
identifying the classical Pontryagin-Thom collapse map with the abstract dual morphism construction of prop. .
More generally, for an embedding of manifolds, then Atiyah duality identifies the Pontryagin-Thom collapse maps
with the abstract dual morphisms
Remark
Given now an E-∞ ring, then the dual morphism induces under smash product a similar Pontryagin-Thom collapse map, but now not in sphere spectrum-(∞,1)-modules but in -(∞,1)-modules.
The image of this under the -cohomology functor produces
If now one has a Thom isomorphism (-orientation) that identifies the cohomology of the dual object with the original cohomology, then together with produces the Umkehr map
that pushes the -cohomology of to the -cohomology of the point. Analogously if instead of the terminal map we start with a more general map .
More generally a Thom isomorphism may not exists, but may still be equivalent to a twisted cohomology-variant of , namely to , where is an (flat) -(∞,1)-module bundle on and and is the (∞,1)-colimit (the generalized Thom spectrum construction). In this case the above yields a twisted Umkehr map.
Properties
General
Proposition
For given all collapse maps for different choices of tubular neighbourhood are homotopic.
Proof
By the fact that the space of tubular neighbourhoods (see there for details) is contractible.
Relation between cohomotopy and cobordism
For a closed smooth manifold of dimension , the Pontryagin-Thom construction (e.g. Kosinski 93, IX.5) identifies the set
of cobordism classes of closed and normally framed submanifolds of dimension inside with the cohomotopy of in degree
(e.g. Kosinski 93, IX Theorem (5.5))
In particular, by this bijection the canonical group structure on cobordism groups in sufficiently high codimension (essentially given by disjoint union of submanifolds) this way induces a group structure on the cohomotopy sets in sufficiently high degree.
Related concepts
The following terms all refer to essentially the same concept:
References
Pontrjagin-Thom construction
Pontrjagin’s construction
General
The Pontryagin theorem, i.e. the unstable and framed version of the Pontrjagin-Thom construction, identifying cobordism classes of normally framed submanifolds with their Cohomotopy charge in unstable Borsuk-Spanier Cohomotopy sets, is due to:
-
Lev Pontrjagin, Classification of continuous maps of a complex into a sphere, Communication I, Doklady Akademii Nauk SSSR 19 3 (1938) 147-149
-
Lev Pontryagin, Homotopy classification of mappings of an (n+2)-dimensional sphere on an n-dimensional one, Doklady Akad. Nauk SSSR (N.S.) 19 (1950), 957–959 (pdf)
(both available in English translation in Gamkrelidze 86),
as presented more comprehensively in:
- Lev Pontrjagin, Smooth manifolds and their applications in Homotopy theory, Trudy Mat. Inst. im Steklov, No 45, Izdat. Akad. Nauk. USSR, Moscow, 1955 (AMS Translation Series 2, Vol. 11, 1959) (doi:10.1142/9789812772107_0001, pdf)
The Pontrjagin theorem must have been known to Pontrjagin at least by 1936, when he announced the computation of the second stem of homotopy groups of spheres:
- Lev Pontrjagin, Sur les transformations des sphères en sphères (pdf) in: Comptes Rendus du Congrès International des Mathématiques – Oslo 1936 (pdf)
Review:
-
Daniel Freed, Karen Uhlenbeck, Appendix B of: Instantons and Four-Manifolds, Mathematical Sciences Research Institute Publications, Springer 1991 (doi:10.1007/978-1-4613-9703-8)
-
Glen Bredon, chapter II.16 of: Topology and Geometry, Graduate Texts in Mathematics 139, Springer (1993) [doi:10.1007/978-1-4757-6848-0, pdf]
-
Antoni Kosinski, chapter IX of: Differential manifolds, Academic Press (1993) [pdf, ISBN:978-0-12-421850-5]
-
John Milnor, Chapter 7 of: Topology from the differentiable viewpoint, Princeton University Press, 1997. (ISBN:9780691048338, pdf)
-
Mladen Bestvina (notes by Adam Keenan), Chapter 16 in: Differentiable Topology and Geometry, 2002 (pdf)
-
Michel Kervaire, La méthode de Pontryagin pour la classification des applications sur une sphère, in: E. Vesentini (ed.), Topologia Differenziale, CIME Summer Schools, vol. 26, Springer 2011 (doi:10.1007/978-3-642-10988-1_3)
-
Rustam Sadykov, Section 1 of: Elements of Surgery Theory, 2013 (pdf, pdf)
-
András Csépai, Stable Pontryagin-Thom construction for proper maps, Period Math Hung 80, 259–268 (2020) (arXiv:1905.07734, doi:10.1007/s10998-020-00327-0)
Discussion of the early history:
Twisted/equivariant generalizations
The (fairly straightforward) generalization of the Pontrjagin theorem to the twisted Pontrjagin theorem, identifying twisted Cohomotopy with cobordism classes of normally twisted-framed submanifolds, is made explicit in:
- James Cruickshank, Lemma 5.2 using Sec. 5.1 in: Twisted homotopy theory and the geometric equivariant 1-stem, Topology and its Applications Volume 129, Issue 3, 1 April 2003, Pages 251-271 (doi:10.1016/S0166-8641(02)00183-9)
A general equivariant Pontrjagin theorem – relating equivariant Cohomotopy to normal equivariant framed submanifolds – remains elusive, but on free G-manifolds it is again straightforward (and reduces to the twisted Pontrjagin theorem on the quotient space), made explicit in:
- James Cruickshank, Thm. 5.0.6, Cor. 6.0.13 in: Twisted Cobordism and its Relationship to Equivariant Homotopy Theory, 1999 (pdf, pdf)
In negative codimension
In negative codimension, the Cohomotopy charge map from the Pontrjagin theorem gives the May-Segal theorem, now identifying Cohomotopy cocycle spaces with configuration spaces of points:
-
Peter May, The geometry of iterated loop spaces, Springer 1972 (pdf)
-
Graeme Segal, Configuration-spaces and iterated loop-spaces, Invent. Math. 21 (1973), 213–221. MR 0331377 (pdf)
c Generalization of these constructions and results is due to
-
Dusa McDuff, Configuration spaces of positive and negative particles, Topology Volume 14, Issue 1, March 1975, Pages 91-107 (doi:10.1016/0040-9383(75)90038-5)
-
Carl-Friedrich Bödigheimer, Stable splittings of mapping spaces, Algebraic topology. Springer 1987. 174-187 (pdf, pdf)
Thom’s construction
Thom's theorem i.e. the unstable and oriented version of the Pontrjagin-Thom construction, identifying cobordism classes of normally oriented submanifolds with homotopy classes of maps to the universal special orthogonal Thom space , is due to:
- René Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28, (1954). 17-86 (doi:10.1007/BF02566923, dml:139072, digiz:GDZPPN002056259, pdf)
Textbook accounts:
- Robert Stong, Notes on Cobordism theory, 1968 (toc pdf, publisher page)
Lashof’s construction
The joint generalization of Pontryagin 38a, 55 (framing structure) and Thom 54 (orientation structure) to any family of tangential structures (“(B,f)-structure”) is first made explicit in
- Richard Lashof, Poincaré duality and cobordism, Trans. AMS 109 (1963), 257-277 (doi:10.1090/S0002-9947-1963-0156357-4)
and the general statement that has come to be known as the Pontryagin-Thom isomorphism (identifying the stable cobordism classes of normally (B,f)-structured submanifolds with homotopy classes of maps to the Thom spectrum Mf) is really due to Lashof 63, Theorem C.
Textbook accounts:
-
Theodor Bröcker, Tammo tom Dieck, Satz 3.1 & 4.9 in: Kobordismentheorie, Lecture Notes in Mathematics 178, Springer (1970) [ISBN:9783540053415]
-
Stanley Kochman, section 1.5 of: Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996
-
Yuli Rudyak, On Thom spectra, orientability and cobordism, Springer Monographs in Mathematics (1998) [doi:10.1007/978-3-540-77751-9, pdf]
Lecture notes:
-
John Francis, Topology of manifolds course notes (2010) (web), Lecture 3: Thom’s theorem (pdf), Lecture 4 Transversality (notes by I. Bobkova) (pdf)
-
Cary Malkiewich, Section 3 of: Unoriented cobordism and , 2011 (pdf)
-
Tom Weston, Part I of An introduction to cobordism theory (pdf)
See also:
See also:
-
Ralph Cohen, John Klein, Umkehr Maps (arXiv:0711.0540)
-
Victor Snaith, Stable homotopy around the arf-Kervaire invariant, Birkhauser 2009
The general abstract formulation in stable homotopy theory is in sketched in section 9 of
- Matthew Ando, Andrew Blumberg, David Gepner, Twists of K-theory and TMF, in Robert S. Doran, Greg Friedman, Jonathan Rosenberg, Superstrings, Geometry, Topology, and -algebras, Proceedings of Symposia in Pure Mathematics vol 81, American Mathematical Society (arXiv:1002.3004)
and is in section 10 of
- Matthew Ando, Andrew Blumberg, David Gepner, Parametrized spectra, multiplicative Thom spectra, and the twisted Umkehr map (arXiv:1112.2203)
with an emphases on parameterized spectra.
Stratified versions
Instead of relating (structured) cobordisms with homs into Thom spectra, one may also relate stratified cobordisms with homs into cell complexes. A version of this relation is spelled out in Section VII.4 of:
- Sandro Buonchristiano, Colin Rourke, and Brian Sanderson. A geometric approach to homology theory. Vol. 18. Cambridge University Press, 1976.
The stratified Pontrjagin-Thom construction may also be considered in higher categorical terms, where it relates functors between geometric computads to manifold diagrams. This is discussed at:
- Christoph Dorn, The categorical Pontryagin-Thom construction. link
Last revised on March 9, 2023 at 12:00:10. See the history of this page for a list of all contributions to it.